无向图的割顶与桥总结

割顶和桥：对于无向图G，如果删除某个节点u后，连通分量数目增加，则称u为图的割顶；如果删除某条边后，连通分量数目增加，则称该边为图的桥。对于连通图删除割顶或桥后都会使得图不再连通

以下我，我们利用dfs的性质来快速找出一个连通图中的所有的割顶和桥 
首先我们要引入”时间戳”这个概念：

时间戳：表示在进行dfs时，每个节点被访问的先后顺序。每个节点会被标记两次，分别用pre[],和post[]表示。 
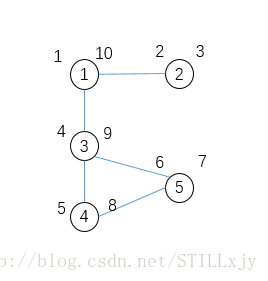
例如下图的时间戳表示：（节点左上角为pre[],右上角为post[],子节点的访问顺序按照编号从小到达访问） 

图中的边分类： 
树边与反向边：在进行dfs时某条边u-v,若v还没有被访问，则u-v为树边，若v已经被访问过则u-v为反向边。 
对于上图的DFS树，下图中实线为树边，虚线为反向边 
 
在无向图中除了树边就是反向边，且不存在跨越两棵子树的边 
所以对于根节点而言，如果有两个及以上节点则根节点为割顶，否则不是 
对于其他节点：在无向连通图G的DFS树中，非根节点u是割顶当且仅当u存在一个子节点v，使得v及其所有后代都没有反向边连回u的祖先（不包括u） 
以上判断条件很好想，只要随便画画草图就可以了

了解以上知识后我们找出图中所有的割顶和桥 
设low[u]为u及其后代所能连回的最早的祖先的pre[]值，则当u存在一个子节点v使得low[v] >= pre[u]时u就为割顶 

同理当 low[v] > pre[u]时 u-v为桥

参考刘汝佳老师的白书上的代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 105, maxm = maxn * 2;
int n, m, tot, dfs_clock;
int h[maxn], dfn[maxn], low[maxn], iscut[maxn];
struct edge
{
    int v, next;
}a[maxm];
void add(int x, int y)
{
    a[tot].v = y;
    a[tot].next = h[x];
    h[x] = tot++;
}
int dfs(int u, int fa)
{
    int lowu = dfn[u] = ++dfs_clock;//注意这里一定是++dfs_clock,不然后来判断新搜到的节点有没有访问过就会出错。
    int child = 0;
    for (int i = h[u]; ~i; i = a[i].next)
    {
        int v = a[i].v;
        if (!dfn[v])//如果这个节点我还没有访问过，树边
        {
            child++;
            int lowv = dfs(v, u);
            lowu = min(lowu, lowv);
            if (lowv >= dfn[u])//割顶的判断
            {
                iscut[u] = 1;//代表该点为割顶
            }
            if (lowv > dfn[u])//桥的判断
            {
                printf("%d - %d
", u, v);//桥和割点的判断略有不同
            }
        }
        else if (dfn[v] < dfn[u] && v != fa)//反向边
        {
            lowu = min(lowu, dfn[v]);
        }
    }
    if (fa == 0 && child == 1)//排除根节点的特殊情况。
    {
        iscut[u] = 0;
    }
    low[u] = lowu;
    return lowu;
}
int main()
{
    //freopen("无向图的割顶和桥.in","r",stdin);
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h); tot = dfs_clock = 0;
    for (int i = 1; i <= m; i++)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        add(x, y); add(y, x);
    }
    dfs(1, 0);
    for (int i = 1; i <= n; i++)
        if (iscut[i])
            printf("%d ", i);
    return 0;
}