
1 二分图
二分图:又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边所关联的两个顶点i和j分别属于这两个不同的顶点集(i∈A, j∈B),则称图G为一个二分图。
简单来说,如果图中所有顶点可以被分为两个集合,图中所有的边的头和尾不属于同一个顶点集合,而是跨越两个集合,则这个图是一个二分图。
例如:图1.1所示的图,无论如何划分顶点集合,也不能保证所有边的头和尾隶属于不同集合,因此,图1.1所示的图不是二分图。
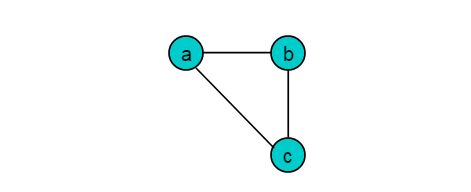
例如:图1.2所示的无向图:
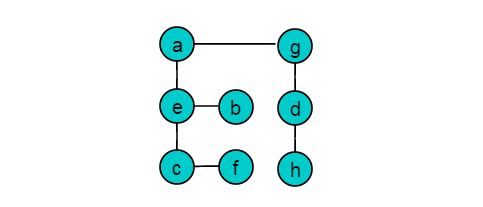
将顶点a,b,c,d作为集合A,将e,f,g,h作为集合B,将图1.2转化为图1.3所示:
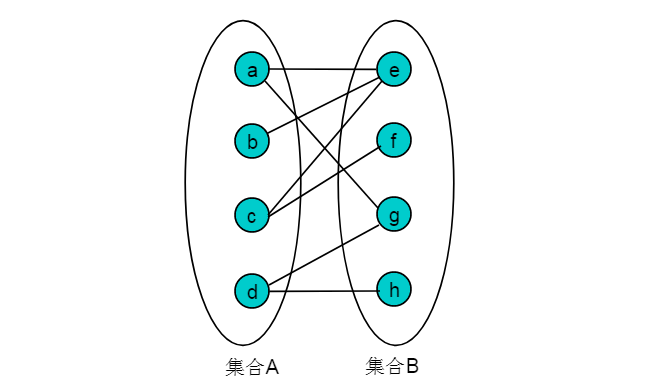
可以看出,图中顶点可以划分为A,B两个集合,而任意一条边的头和尾又分别隶属于集合A和集合B,因此,此图为二分图。
2 匹配
匹配:在图论中,一个匹配(matching)是指一个边的集合,其中任意两条边都没有公共顶点。
例如:图2.1中红色的边,可以为图1.3所示图的一个匹配。
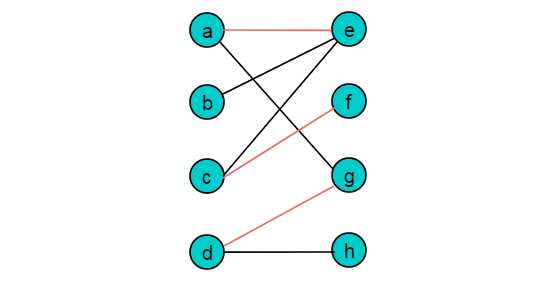
3 最大匹配
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 3.1是一个最大匹配,它包含4条匹配边。
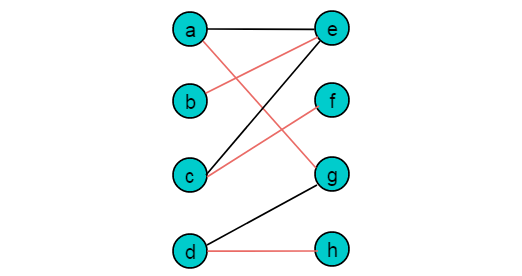
4 完美匹配
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突),但并非每个图都存在完美匹配。
5 交替路径
交替路径:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路径称为交替路径。
6 增广路径
增广路径:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。
增广路径性质:
(1)P的路径长度必定为奇数,第一条边和最后一条边都不属于M,因为两个端点分属两个集合,且未匹配。
(2)P经过取反操作可以得到一个更大的匹配M’。
(3)M为G的最大匹配当且仅当不存在相对于M的增广路径。
7 匈牙利算法
匈牙利算法:利用增广路径求二分图的最大匹配算法称作匈牙利算法。(匈牙利数学家Edmonds于1965年提出)。
基本思想:通过寻找增广路径,把增广路径中的匹配边和非匹配边的相互交换,这样就会多出一条匹配边,直到找不到增广路径为止。
例如:以图2.1所示的二分图为例,使用匈牙利算法求解图的最大匹配。
(1)从顶点a出发,按照交替路径前进,第一个非匹配边为,到达顶点e,e为非匹配点,构成增广路径。令为匹配边,顶点a,e为匹配顶点。
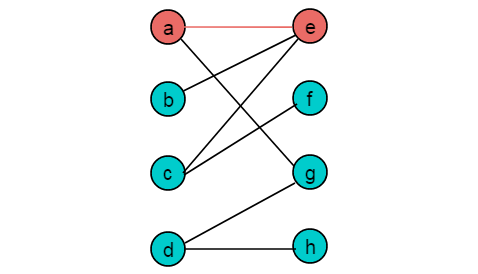
(2)从顶点b出发,第一非匹配边为 ,到达顶点e,选择匹配边,到达a,选择非匹配边,g为非匹配点,找到一条增广路径。

(3)交换增广路径中的匹配边与非匹配边,得到如下匹配。
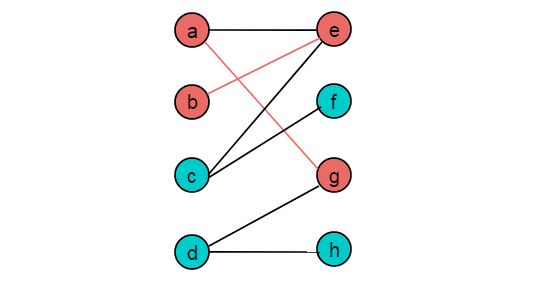
(4)从顶点c出发,第一非匹配边为,到达顶点e,然后按照交替路径前进,到达顶点b,无法继续前进。
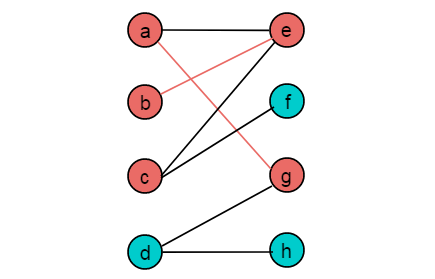
(5)从顶点c出发,选择第二条非匹配边。
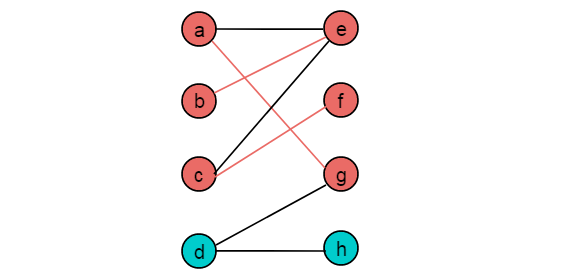
(6)从顶点d出发,选择非匹配边,到达顶点g,选择匹配边,到达顶点a,选择非匹配边到达顶点e,选择匹配边,到达顶部b,没有可以选择的边,且没有找到增广路径。
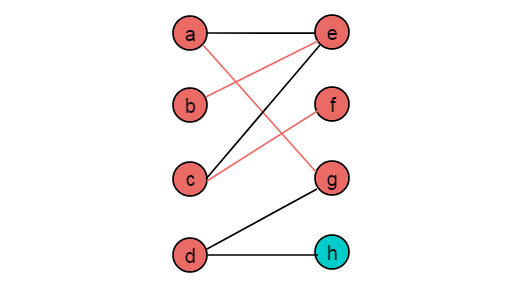
(7)继续从顶点d出发,选择非匹配边,找到增广路径,将边变为匹配边,算法结束。
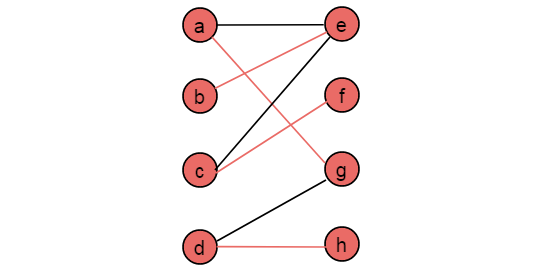
8 结语
匈牙利算法多用于指派问题中,例如任务匹配问题。通过转化为二分图的形式,求解最大匹配,保证实现最优分配。
