点击蓝色“五分钟学算法”关注我哟
加个“星标”,一起学算法

慢速排序
慢速排序算法在 1986 年由 Andrei Broder 和 Jorge Stolfi 发表,主要采取了分治和递归的思想:
具体的操作是分为以下两大步:
找出最大者
将其余的数排序
其中子问题 1 又可分为以下 3 小步:
1.1 找出前 n/2 个数中的最大者
1.2 找出后 n/2 个数中的最大者
1.3 取这两个最大者中的较大者
最后,子问题 1.1 和 1.2 的解决方法是,将相应的数排序后取最后一个。
也就是说我们把原问题分解成 3 个稍微容易一点点的子问题:给前一半数排序,给后一半数排序,给除了一个数以外的其它数排序。递归地进行这一系列步骤,直到至多只剩下一个元素时,停止。
动画描述
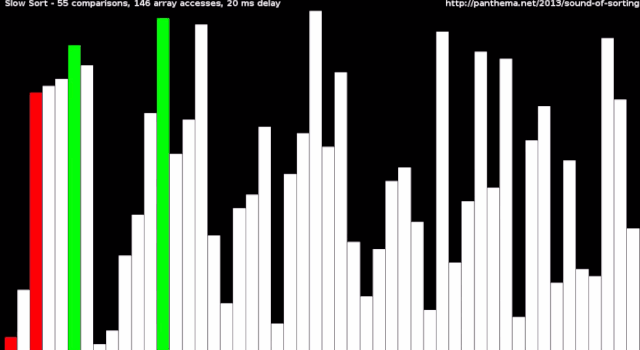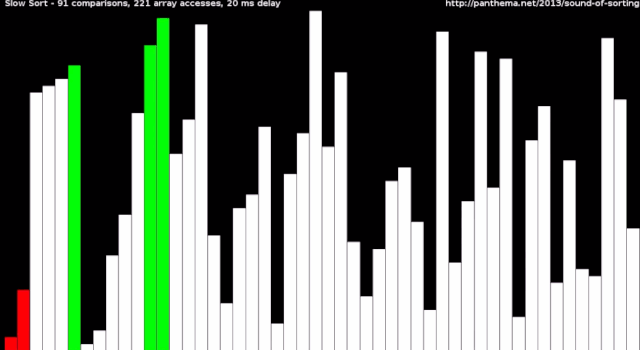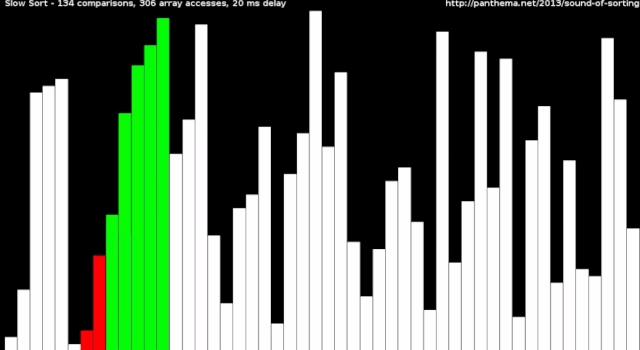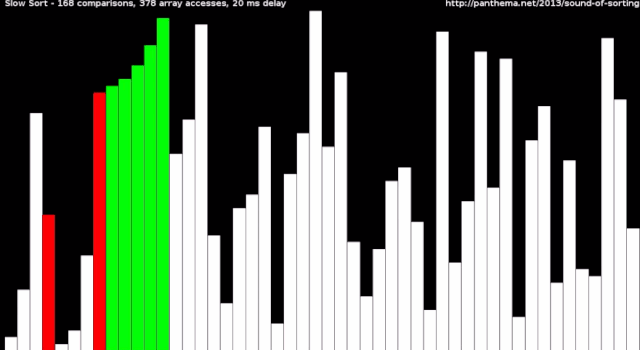
slow sort from Timo Bingmann
国外有人对慢速排序动画写了一个段子:
slow sort is just merge sort with the severe paranoia that the elements have moved themselves while it wasn't looking.
排序的元素趁大家不注意的时候偷偷的移动一下。
代码实现
procedure slowsort(A,i,j) if i >= j then return m = (i + j) / 2 slowsort(A,i,m) // 先排序前半段 slowsort(A,m + 1,j) // 再排序后半段 if A[j] < A[m] then swap A[j] and A[m] // 找到最大数,放到末尾 slowsort(A,i,j - 1) // 再排序除了最大数之外的数据return
m = (i + j) / 2
slowsort(A,i,m) // 先排序前半段
slowsort(A,m + 1,j) // 再排序后半段
if A[j] < A[m] then swap A[j] and A[m] // 找到最大数,放到末尾
slowsort(A,i,j - 1) // 再排序除了最大数之外的数据
时间复杂度
通过代码与动画可以看出,慢速排序和其他排序算法效果一样,可以将一个无序数据集合进行合理排序。
但是,它的时间复杂度简直吓人!
T(n) = 2 * T(n/2) + T(n-1) + C( C 表示常量时间)
你可以通过下面三张图来理解这个时间复杂度的有多夸张!(以下图片来源于网络)


原 创 热 文 推 荐
 你点的每个“在看”,我都认真当成了喜欢
你点的每个“在看”,我都认真当成了喜欢