给你一个有向图,然后给你起点和终点,问你从起点到终点有多少个关键点,如果当前的这个点删除了就无法从起点到终点,那么这个点就是一个关键点..
思路:
(1)有两种做法,我用的是最大流的,另一种是先跑最短路然后搜索,先说最大流,最大流的很容易理解,首先我们拆点建图,每个点拆成两个点,限流是1,然后起点和终点的限流是2,点于点之间是INF,跑一遍最大流,如果流量是0,说明不连接,那么所有的点都是关键点,输出n,如果流量是2那么说明最小割是2,也就是说无论你把那个点删除都不影响连通性,所以只有起点和终点是关键点,如果流量是1,那也就是说在路途中可能存在关键点,那么我们就
用暴力搜索的方式去找这些关键点,对于搜索这块我自己卡了两天了,今天才弄明白,首先我们定义跑完最大流后流量为0的边为关键边,首先第一个点一定是关键点,我们一个一个找,我的理解是 从当前的这个关键点出发,通过非关键边搜索,第一个搜索不到的点一定是关键点,这里的搜索不到的点指的是我们比如当前边u,v,他沿着非关键边无法从u走到v,但是沿着关键边可以走到,那么v就是第一个搜不到的点,v一定是关键点,跑完最大流后,流量0(正向)的是关键路径上的点,非0的是非关键路径上的点,我们每次从当前的关键点出发,沿着流量非0的跑,把这次跑到的点全记录下来,mark上,然后枚举每一个搜到的点相邻的点,如果是流量0,那么这个就是第一个到达不了的点,那么他一定是关键点,这届break,以这个点为起点在接着搜索,就这样一直找到T为止.还有为什么上面有两条边是2而不是别的,是为了缩短时间,2最多两次,我们是为了找到答案是0,1,还是其他,2.3.4..都是其他,都是只存在两个关键点的,所以我们要节省时间,流量2,如果弄大了答案肯定对,但会TLE...
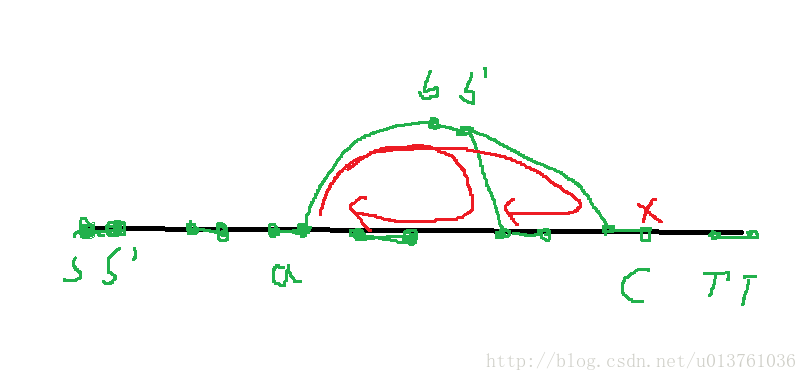
最大流已知当前点找下一个关键点的搜索过程,红色是搜索路径,当前点a,下一个关键点是c,
则如图:
#pragma comment(linker, "/STACK:1024000000,1024000000") #include<stdio.h> #include<string.h> #include<queue> #define N_node 200000 + 20 #define N_edge 600000 + 60 #define INF 1000000000 using namespace std; typedef struct { int to ,cost ,next; }STAR; typedef struct { int x ,t; }DEP; STAR E[N_edge]; DEP xin ,tou; int list[N_node] ,tot; int deep[N_node] ,list2[N_node]; int mark[N_node] ,num[N_node] ,tt; void add(int a, int b ,int c) { E[++tot].to = b; E[tot].cost = c; E[tot].next = list[a]; list[a] = tot; E[++tot].to = a; E[tot].cost = 0; E[tot].next = list[b]; list[b] = tot; } int minn(int x ,int y) { return x < y ? x : y; } bool BFS(int s ,int t ,int n) { memset(deep ,255 ,sizeof(deep)); deep[s] = 0; xin.x = s; xin.t = 0; queue<DEP>q; q.push(xin); while(!q.empty()) { tou = q.front(); q.pop(); for(int k = list[tou.x] ;k ;k = E[k].next) { xin.x = E[k].to; xin.t = tou.t + 1; if(deep[xin.x] != -1 || !E[k].cost) continue; deep[xin.x] = xin.t; q.push(xin); } } for(int i = 0 ;i <= n ;i ++) list2[i] = list[i]; return deep[t] != -1; } int DFS_FLOW(int s ,int t ,int flow) { if(s == t) return flow; int nowflow = 0; for(int k = list2[s] ;k; k = E[k].next) { list2[s] = k; int to = E[k].to; int cost = E[k].cost; if(deep[to] != deep[s] + 1 || !cost) continue; int tmp = DFS_FLOW(to ,t ,minn(cost ,flow - nowflow)); nowflow += tmp; E[k].cost -= tmp; E[k^1].cost += tmp; if(flow == nowflow) break; } if(!nowflow) list2[s] = 0; return nowflow; } int DINIC(int s ,int t ,int n) { int sum = 0; while(BFS(s ,t ,n)) { sum += DFS_FLOW(s ,t ,INF); } return sum; } void dfs(int s) { mark[s] = 1; num[++tt] = s; for(int k = list[s] ;k ;k = E[k].next) { int to = E[k].to; if(E[k].cost && !mark[to]) dfs(to); } } int find(int n ,int S ,int T) { E[list[S]].cost = 0; E[list[T - n]].cost= 0; int cout = 0; memset(mark ,0 ,sizeof(mark)); while(1) { tt = 0; dfs(S); int ok = 1; for(int i = 1 ;i <= tt && ok ;i ++) { for(int k = list[num[i]] ;k && ok ;k = E[k].next) if(k % 2 == 0 && !mark[E[k].to] && !E[k].cost) { ok = 0; S = E[k].to; cout ++; if(E[k].to == T) return cout; } } } } int main () { int n ,m ,S ,T ,i ,j ,a ,b ,c; while(~scanf("%d %d" ,&n ,&m)) { memset(list ,0 ,sizeof(list)); tot = 1; for(i = 1 ;i <= m ;i ++) { scanf("%d %d" ,&a ,&b); add(a + n + 1,b + 1, INF); } scanf("%d %d" ,&S ,&T); S ++ ,T ++; for(i = 1 ;i <= n ;i ++) { if(i != S && i != T) add(i ,i + n ,1); else add(i ,i + n ,2); } T += n; int flow = DINIC(S ,T ,n + n); if(flow == 0) printf("%d " ,n); else if(flow == 2) puts("2"); else printf("%d " ,find(n ,S ,T)); } return 0; }
思路:
(2)最短路,先跑一个最短路,记录路径,如果到不了T,那么就输出n,如果能的话,来一个深搜,看看只跑非最短路上的点能不能到达T,如果能,那么就说明至少存在两条不相交的路,那么直接输出2,否则就是存在关键点的情况了,枚举每一个关键点,通过非最短路上的点找到里关键点最远的那个最短路上的点,那么这个点一定是关键点,然后在吧当前的这个点当下一步的关键点,就这样一直找到T就行了..比最大流的那个好写,思路都差不多..
当前点a的下一个关键路径是c,是最远的那一个,如图.
#include<stdio.h> #include<string.h> #include<queue> #define N_node 110000 #define N_edge 330000 #define INF 1000000000 using namespace std; typedef struct { int to ,next ,cost; }STAR; STAR E[N_edge]; int list[N_node] ,tot; int mer[N_node] ,S ,T; int s_x[N_node] ,mk_sx[N_node]; int mark[N_node]; void add(int a ,int b ,int c) { E[++tot].to = b; E[tot].cost = c; E[tot].next = list[a]; list[a] = tot; } bool SPFA(int s ,int t ,int n) { memset(mark ,0 ,sizeof(mark)); for(int i = 0 ;i <= n ;i ++) { s_x[i] = INF; mer[i] = i; } s_x[s] = 0; mark[s] = 1; queue<int>q; q.push(s); while(!q.empty()) { int xin ,tou; tou = q.front(); q.pop(); mark[tou] = 0; for(int k = list[tou] ;k ;k = E[k].next) { xin = E[k].to; if(s_x[xin] > s_x[tou] + E[k].cost) { s_x[xin] = s_x[tou] + E[k].cost; mer[xin] = tou; if(!mark[xin]) { mark[xin] = 1; q.push(xin); } } } } return s_x[t] != INF; } int ok; void DFS_1(int s) { for(int k = list[s] ;k ;k = E[k].next) { int to = E[k].to; if(mark[to]|| ok) continue; if(to == T) ok = 1; if(mk_sx[to] || ok) continue; mark[to] = 1; DFS_1(to); } } int mk_id ,maxx; void DFS_2(int s) { for(int k = list[s] ;k ;k = E[k].next) { int to = E[k].to; if(mark[to]) continue; if(mk_sx[to]) { if(maxx < s_x[to]) { maxx = s_x[to]; mk_id = to; } continue ; } mark[to] = 1; DFS_2(to); } } int main () { int n ,m ,i ,j; int a ,b; while(~scanf("%d %d" ,&n ,&m)) { memset(list ,0 ,sizeof(list)); tot = 1; for(i = 1 ;i <= m ;i ++) { scanf("%d %d" ,&a ,&b); add(a + 1 ,b + 1 ,1); } scanf("%d %d" ,&S ,&T); S ++ ,T ++; if(!SPFA(S ,T ,n)) { printf("%d " ,n); continue; } memset(mk_sx ,0 ,sizeof(mk_sx)); int now = T; while(mer[now] != now) { mk_sx[now] = 1; now = mer[now]; } mk_sx[now] = 1; ok = 0; memset(mark ,0 ,sizeof(mark)); mark[S] = 1; DFS_1(S); if(ok) { puts("2"); continue; } int sum = 1; memset(mark ,0 ,sizeof(mark)); while(1) { //mk_id ,maxx maxx = 0; mark[S] = 1; DFS_2(S); sum ++; S = mk_id; //printf("%d*** " ,S); if(S == T) break; } printf("%d " ,sum); } return 0; }