使用广度优先算法找到最短路径,只有3段,但不一定是最快路径。如下图给每段加上时间,会发现双子峰->A->D->金门大桥是并不是用时最少的。
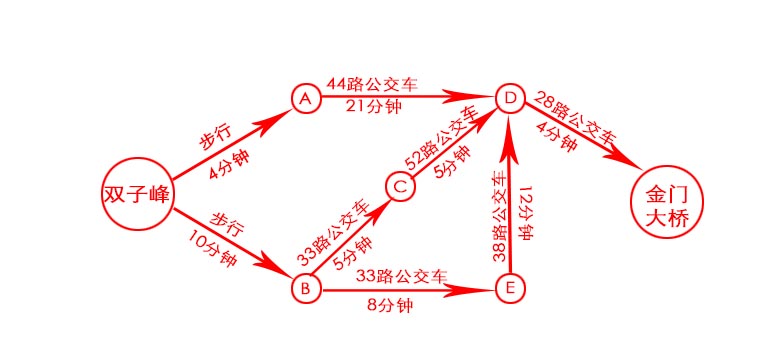
如果要找出最快的路径,可使用迪克斯特拉算法
1.使用迪克斯特拉算法
步骤:
- 1.找出最便宜的节点,即可在最短时间内到达的节点
- 2.更新该节点的邻居的开销
- 3.重复这个过程,直到对图中的每个节点都这样做了
- 4.计算最终路径
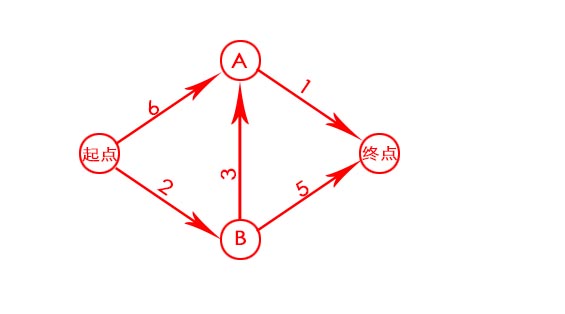
第一步:找出最便宜的节点
站在起点,起点的邻居为A和B,前往A点需要6分钟,前往B点需要2分钟。终点不能直接到达,设为无穷大∞。因此最便宜的节点为B
第二步:计算经节点B前往其各个邻居所需的时间
B的邻居为A和终点,前往A需要3分钟,前往终点需要5分钟。
前往A:2+3=5 < 6,更新A的花销
前往终点:2+5=7 < ∞,更新终点的花销
第三步:重复。除节点B外,最便宜的节点的为A,计算经节点A前往其各个邻居所需的时间
A的邻居为终点,前往终点需要1分钟。
前往终点:5+1=6 < 7,更新前往终点的花销。
第四步:计算最终路径
起点-B-A-终点,最短用时6分钟
| 节点 | 起点的邻居 | B的邻居 | A的邻居 |
| A | 2+3=5 | ||
| B | 2 | ||
| 终点 | 5+1=6 |
2.术语
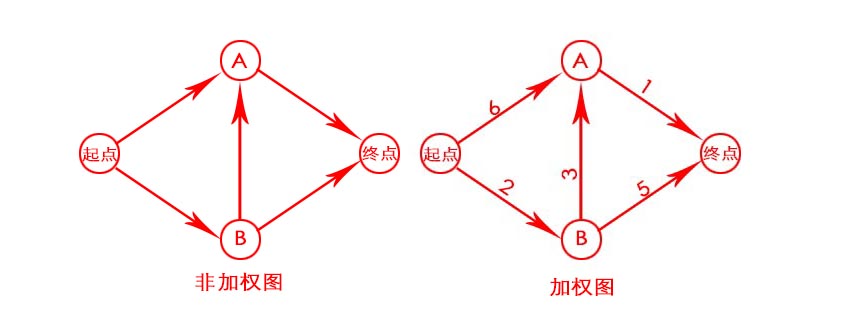
每条边都有关联数字的图,这些数字称为权重。
带权重的图称为加权图,不带权重的图称为非加权图。
要计算非加权图中的最短路径,使用广度优先搜索。
要计算加权图中的最短路径,使用迪克斯特拉算法。
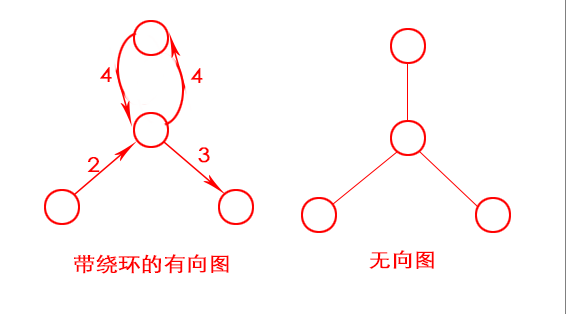
图可能有环,意味着你从一个节点出发,走一圈又回到这个节点。每绕环1次,总权重就增加8。
在无向图中,每条边都是一个环。
因此迪克斯特拉算法只使用于有向无环图
3.换钢琴
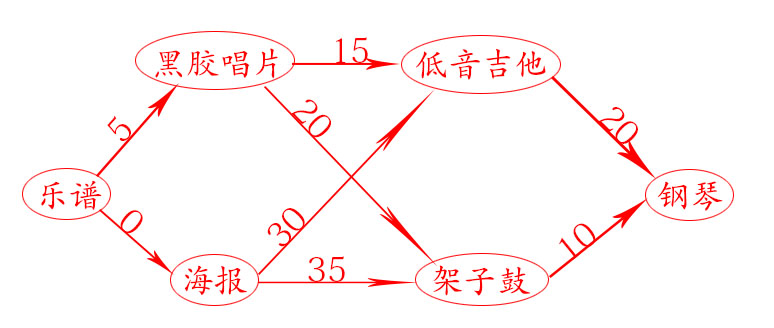
1.由起点出发,先找出最便宜的节点海报,并更新其邻居的开销
2.由起点出发,找出剩余最便宜的节点唱片,并更新其邻居的开销
3.下一个最便宜的节点吉他,开销是20,更新其邻居的开销
4.更新剩余最便宜的节点架子鼓,更新其邻居的开销。
| 节点 | 起点(乐谱) | 海报(父节点) | 唱片(父节点) | 吉他(父节点) | 架子鼓(父节点) |
| 唱片 | 5 | ||||
| 海报 | 0 | ||||
| 吉他 | 20 | ||||
| 架子鼓 | 25 | ||||
| 钢琴 | 35 |
4.负权边
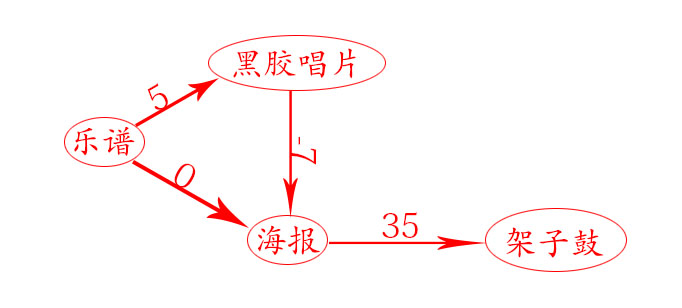
1.起点出发,寻找最便宜的节点海报,更新其邻居开销
2.起点出发,寻找剩余最便宜的节点唱片,更新其邻居海报开销为-2
海报节点已经被处理过,处理唱片节点时却更新了其开销。这是危险的信号。节点一旦被处理,就意味着没有前往该节点的更便宜途径,但却找到了前往海报节点的更便宜途径。因此,不能将迪克斯特拉算法用于包含负权边的图。
在包含负权边的图中,要找出最短路径,可食用另一种算法-贝尔曼-福德算法。
| 节点 | 起点(乐谱) | 海报(父节点) | 唱片 |
| 唱片 | 5 | ||
| 海报 | 0 | -2 | |
| 架子鼓 | 35 |
5.实现
#graph用于存储节点和对应的开销
graph={
"start":{
"a":6,
"b":2
},
"a":{
"end":1
},
"b":{
"a":3,
"end":5
},
"end":{}
}
infinity=float("inf")
#costs用于存储每个节点的开销
costs={
"a":6,
"b":2,
"end":infinity
}
#processed用于存储已处理过的节点
processed=[]
#parents用于存储父节点
parents={
"a":"start",
"b":"start",
"end":None
}
#返回开销最低的节点
def find_lowest_cost_node(costs):
#传入一个字典
lowest_cost=float("inf")
lowsest_cost_node=None
for node in costs.keys():
#对字典进行遍历,返回未处理且开销最小的节点
cost = costs[node]
if cost < lowest_cost and node not in processed:
lowest_cost = cost
lowsest_cost_node = node
return lowsest_cost_node
node = find_lowest_cost_node(costs)
while node is not None:
#只要有未处理的节点,就循环
cost = costs[node]
neighbors = graph[node]
#对节点的邻居n更新开销
for n in neighbors.keys():
new_cost = cost + neighbors[n]
if costs[n] > new_cost:
costs[n] = new_cost
parents[n] = node
processed.append(node)
node = find_lowest_cost_node(costs)
print(costs["end"]) #6