Codeforces Round #409 (rated, Div. 2, based on VK Cup 2017 Round 2) C. Voltage Keepsake二分

C. Voltage Keepsake

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You have n devices that you want to use simultaneously.

The i-th device uses ai units of power per second. This usage is continuous. That is, in λ seconds, the device will use λ·ai units of power. The i-th device currently has bi units of power stored. All devices can store an arbitrary amount of power.

You have a single charger that can plug to any single device. The charger will add p units of power per second to a device. This charging is continuous. That is, if you plug in a device for λ seconds, it will gain λ·p units of power. You can switch which device is charging at any arbitrary unit of time (including real numbers), and the time it takes to switch is negligible.

You are wondering, what is the maximum amount of time you can use the devices until one of them hits 0 units of power.

If you can use the devices indefinitely, print -1. Otherwise, print the maximum amount of time before any one device hits 0 power.

Input

The first line contains two integers, n and p (1 ≤ n ≤ 100 000, 1 ≤ p ≤ 109) — the number of devices and the power of the charger.

This is followed by n lines which contain two integers each. Line i contains the integers ai and bi (1 ≤ ai, bi ≤ 100 000) — the power of the device and the amount of power stored in the device in the beginning.

Output

If you can use the devices indefinitely, print -1. Otherwise, print the maximum amount of time before any one device hits 0 power.

Your answer will be considered correct if its absolute or relative error does not exceed 10 - 4.

Namely, let's assume that your answer is a and the answer of the jury is b. The checker program will consider your answer correct if .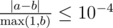

Examples

input

2 1
2 2
2 1000

output

2.0000000000

input

1 100
1 1

output

-1

input

3 5
4 3
5 2
6 1

output

0.5000000000

Note

In sample test 1, you can charge the first device for the entire time until it hits zero power. The second device has enough power to last this time without being charged.

In sample test 2, you can use the device indefinitely.

In sample test 3, we can charge the third device for 2 / 5 of a second, then switch to charge the second device for a 1 / 10 of a second.

题目大意：给你n台机器，每个机器每单位时间消耗a[i]个能量，起初有b[i]个单位的能量。你有一个充电器，可以给一个机器每单位时间充p个能量。问你如果

　　　　 这些机器一起工作，最多能工作多次时间

题目解析：二分答案为time，我们可以得到充电器能充的能量为time*p，然后扫一遍，如果机器工作时间不够time，则需要消耗的能量为 time*a[i]-b[i]

　　　　如果充电器能量 < 0则不满足

#include <bits/stdc++.h>

using namespace std;
const int MAXN = 100007;
int n, m, p;
double a[MAXN], b[MAXN], tim[MAXN];
bool slove(double lim){
    double power = lim*p;
    for(int i = 0; i < n; i++){
        if(tim[i] < lim){
            power -= (lim - tim[i])*a[i];
        }
        if(power < 0) return false;
    }
    return true;
}
int main() {
    cin >> n >> p;
    for(int i = 0; i < n; i++) {
        cin >> a[i] >> b[i];
        tim[i] = b[i]/a[i];
    }
    double l = 0, r = 1e14, mid;
    for(int i = 0; i < 100; i++){
        mid = (l+r)/2;
        if(slove(mid)) l = mid;
        else r = mid;
    }
    if(l > 1e13) printf("-1
");
    else printf("%.10f
", l);
    return 0;
}