AtCoder Grand Contest 001 B

B - Mysterious Light

---

Time limit : 2sec / Stack limit : 256MB / Memory limit : 256MB

Score : 500 points

Problem Statement

Snuke is conducting an optical experiment using mirrors and his new invention, the rifle of Mysterious Light.

Three mirrors of length N are set so that they form an equilateral triangle. Let the vertices of the triangle be a,b and c.

Inside the triangle, the rifle is placed at the point p on segment ab such that ap=X. (The size of the rifle is negligible.) Now, the rifle is about to fire a ray of Mysterious Light in the direction of bc.

The ray of Mysterious Light will travel in a straight line, and will be reflected by mirrors, in the same ways as "ordinary" light. There is one major difference, though: it will be also reflected by its own trajectory as if it is a mirror! When the ray comes back to the rifle, the ray will be absorbed.

The following image shows the ray's trajectory where N=5 and X=2.

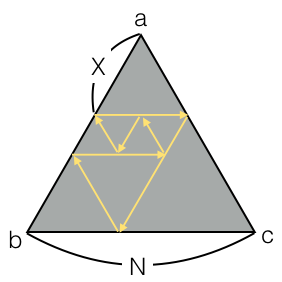
It can be shown that the ray eventually comes back to the rifle and is absorbed, regardless of the values of N and X. Find the total length of the ray's trajectory.

Constraints

• 2≦N≦10¹²
• 1≦X≦N−1
• N and X are integers.

Partial Points

• 300 points will be awarded for passing the test set satisfying N≦1000.
• Another 200 points will be awarded for passing the test set without additional constraints.

---

Input

The input is given from Standard Input in the following format:

N X

Output

Print the total length of the ray's trajectory.

---

Sample Input 1

5 2

Sample Output 1

12

Refer to the image in the Problem Statement section. The total length of the trajectory is 2+3+2+2+1+1+1=12.

欧几里得~题解后补，先上代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll gcd(ll n, ll m) {
    if(n % m== 0) {
        return m;
    }
    return gcd(m, n%m);
}
int main() {
    ios :: sync_with_stdio(false);
    ll N, X, ans;
    cin >> N >> X;
    ans = 3*(N - gcd(N, X));
    cout << ans << endl;
}