关于二叉树
二叉树是一种在面试中也会涉及的到数据结构。
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。二叉树的物种不同的形态如下: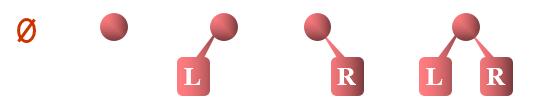
二叉树的结构定义有三个部分组成,分别是值域val和指向左右孩子的指针*left和*right。
1 struct TreeNode { 2 int val; 3 struct TreeNode *left; 4 struct TreeNode *right; 5 TreeNode(int x) : 6 val(x), left(NULL), right(NULL) { 7 } 8 };
面试题:二叉树的镜像
输入二叉树,输出它的镜像。
分析:
树的镜像不是我们所熟知的内容,通常在课本上所熟悉的就是树的遍历等基本的操作。但是我们可以通过图像来把镜像的过程给描述出来。比如像下面的两个二叉树就是互为镜像。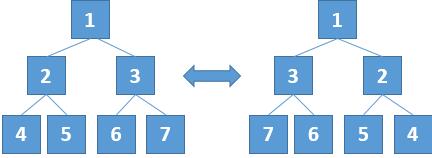
下面我们来分析,镜像发生的过程是怎么样的。
这两个树根结点都是1,那么先交换根结点的左右结点,得到图2。交换后,我们发现,对于结点2和3来说,它们的子结点的左右顺序没有发生变化。因此还要交换对应的结点。对于根结点的左子树,将其视为一棵新的二叉树,同样的交换其子结点。得到图3。同样的作用于右子树,那么最后的交换就完成了。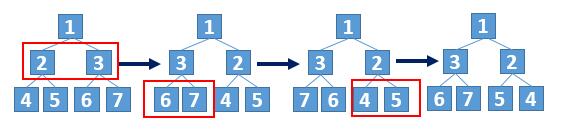
总结上面的几个步骤:我们先先序遍历这个树的子结点,如果子结点有子结点,那么就交换,当交换完成所有的非叶子结点,那么就是我们所要求的镜像。
递归方法
从上面的分析可以看出,递归是解决该问题比较明晰的思路,思考起来也比较能够想到。下面是递归的解决方案。
1 void MirrorRecursively(TreeNode *pRoot) 2 { 3 if((pRoot == NULL) || (pRoot->left == NULL && pRoot->right)) 4 return; 5 6 TreeNode *pTemp = pRoot->left; 7 pRoot->left = pRoot->right; 8 pRoot->right = pTemp; 9 10 if(pRoot->left) 11 MirrorRecursively(pRoot->left); 12 13 if(pRoot->right) 14 MirrorRecursively(pRoot->right); 15 }
非递归方法
扩展一下如果,采用循环,如何实现?递归的实现借助于栈,那么循环,利用栈即可。下面给出代码。
void MirrorIteratively(TreeNode* pRoot) { if(pRoot == NULL) return; std::stack<TreeNode*> stackTreeNode; stackTreeNode.push(pRoot); while(stackTreeNode.size() > 0) { TreeNode *pNode = stackTreeNode.top(); stackTreeNode.pop(); TreeNode *pTemp = pNode->left; pNode->left = pNode->right; pNode->right = pTemp; if(pNode->left) stackTreeNode.push(pNode->left); if(pNode->right) stackTreeNode.push(pNode->right); } }
测试用例
写代码的时候要考虑到各种情况。包括NULL,只有一个结点,普通二叉树,二叉树所有结点只有左结点/右结点等。针对下面几种情况都要满足需求。
