关于栈和队列的考察
栈和队列都是比较常用的数据结构。栈的应用非常的广泛,比如说,递归函数的实现就是借助于栈保存相关的数据。操作系统中每个线程也会使用栈来保存函数调用涉及到的一些参数和其他变量等。栈最大的一个特点就是先进后出(FILO—First-In/Last-Out)。
队列和栈不同的是,队列是一种先进先出(FIFO—first in first out)的数据结构。
对应的STL中都有实现了的方法。
栈的相关方法:
| 入栈,s.push(x) 出栈,s.pop() 访问栈顶,s.top() 判断栈空,s.empty() 访问栈中的元素个数,s.size() |
队列的方法与栈大同小异,列举如下:
| 入队,q.push(x) 出队,q.pop() 访问队首元素,q.front()、访问队尾元素,q.back() 判断队列空,q.empty() 访问队列中的元素个数,q.size() |
注意,两者的pop()方法,仅仅删除栈顶和队列首元素,并不返回,如需截获元素,在pop()方法之前使用top()或者front()方法。
面试题1:
用两个栈实现队列,请实现两个函数appendTail和deleteHead,完成在队列尾部插入结点和在队列首部删除结点的功能。模板定义如下:
1 template <typename T> class CQueue 2 { 3 public: 4 CQueue(void); 5 ~CQueue(void); 6 7 // 在队列末尾添加一个结点 8 void appendTail(const T& node); 9 10 // 删除队列的头结点 11 T deleteHead(); 12 13 private: 14 stack<T> stack1; 15 stack<T> stack2; 16 };
分析:
这道题是要求通过两个“先进后出”的操作完成“先进先出”的功能。下面这个例子比较形象的给出了实现的过程。
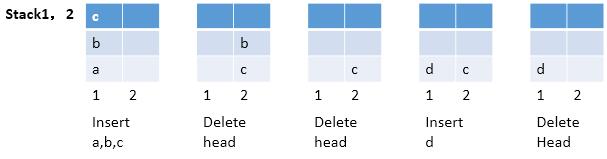
起初的时候,两个栈都为空,那么只要有元素来,那么默认插入到第一个栈。这是,如果要求删除一个元素,那么元素已经不在栈顶,在第一个栈中肯定无法直接删除了,此时我们发现第二个栈还没有派上用场,这里用到了,把第一个栈中的元素压入到第二个栈中,可以发现原来在第一个栈中栈底的元素已经出现在第二个栈的栈顶上,所以删除的功能就实现了。如果这个时候,“队列”里还有元素,我们还可以继续出队,而且,现在要出队的元素就在第二个栈的栈顶,所以直接出栈即可。
分析到现在,下面给出总结:如果栈2不为空,同时又需要出队,那么顺其自然直接弹出即可。如果栈2为空,那么从栈1中逐个弹出压入,那么完整的实现了先进先出的功能。
具体的流程和代码实现如下:
1 template<typename T> void CQueue<T>::appendTail(const T& element) 2 { 3 stack1.push(element); 4 } 5 6 template<typename T> T CQueue<T>::deleteHead() 7 { 8 if(stack2.size()<= 0) 9 { 10 while(stack1.size()>0) 11 { 12 T& data = stack1.top(); 13 stack1.pop(); 14 stack2.push(data); 15 } 16 } 17 18 if(stack2.size() == 0) 19 throw new exception("queue is empty"); 20 21 T head = stack2.top(); 22 stack2.pop(); 23 24 return head; 25 }
面试题2:
用两个队列实现栈。
分析:
结合下图,我们分析一下具体的流程,搞清楚了相关的流程,那么对应的操作就明晰了。
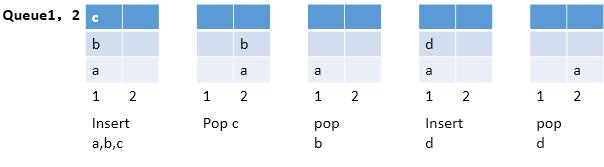
起初的时候,两个队列都是空的,那么当“栈”要压入一个元素,我们就默认将该元素压入到队列1中。接下来继续压入剩余的元素。
接下来考虑,如果我们想要弹出一个元素如何操作。栈中要求出栈的为栈顶元素,那么即为最后插入的元素,但是该元素在队列的尾部,必须要求前面的元素出队后才能访问,说到这里,你也就发现思路的:出队前面的元素,到另一个队列中,那么就可以在原队列中弹出唯一的元素了。
现在我们再考虑另一个情况,队列里面还有元素,“栈”又进来了新的元素,那么就将新元素,压入到存在元素的那一个队列中,剩余的操作,上面已经提到了,一样的操作,看图也许就清晰多了。
1 template <typename T> class CStack 2 { 3 public: 4 CStack(void); 5 ~CStack(void); 6 7 // 在队列末尾添加一个结点 8 void Input(const T& ); 9 10 // 删除队列的头结点 11 T Output(); 12 13 private: 14 queue<T> queue1; 15 queue<T> queue2; 16 };
1 template<typename T> void CStack<T>::Input(const T& t){ 2 if(queue1.empty()&&queue2.empty()) 3 queue1.push(t); 4 else 5 if(!queue1.empty()) 6 queue1.push(t); 7 else 8 queue2.push(t); 9 } 10 11 template<typename T> T CStack<T>::Output(){ 12 T t; 13 if(queue1.empty()&&queue2.empty()) 14 retutn NULL; 15 else 16 if(queue1.empty()){ 17 while(queue2.size()!=1){ 18 queue1.push(queue2.front()); 19 queue2.pop(); 20 } 21 t=queue2.front(); 22 queue2.pop(); 23 } 24 else 25 { 26 while(queue1.size()!=1){ 27 queue2.push(queue1.front()); 28 queue1.pop(); 29 } 30 t=queue1.front(); 31 queue1.pop(); 32 } 33 return t; 34 } 35