迭代法也称辗转法,是一种不断用变量的旧值推出新值的过程。它是解决问题的一种基本方法,通过让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。
迭代算法的基本思想是:为求一个问题的解x,可由给定的一个初值x0,根据某一迭代公式得到一个新的值x1,这个新值x1比初值x0更接近要求的值x;再以新值作为初值,即:x1→x0,重新按原来的方法求x1,重复这一过程直到|x1-x0|<ε(某一给定的精度)。此时可将x1作为问题的解x。
利用迭代算法解决问题,需要做好以下三个方面的工作:
(1)确定迭代变量。在可以用迭代算法解决的问题中,至少存在一个直接或间接地不断由旧值推出新值的变量,这个变量就是迭代变量。
(2)建立迭代关系式。所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系)。迭代关系式的建立是解决迭代问题的关键。
(3)对迭代过程进行控制。在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。不能让迭代过程无休止地重复执行下去。迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来;另一种是所需的迭代次数无法确定。对于前一种情况,可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况,需要进一步分析出用来结束迭代过程的条件。
迭代也是用循环结构实现,只不过要重复的操作是不断从一个变量的旧值出发计算它的新值。其基本格式描述如下:
迭代变量赋初值;
while (迭代终止条件)
{
根据迭代表达式,由旧值计算出新值;
新值取代旧值,为下一次迭代做准备;
}
【例1】验证谷角猜想
日本数学家谷角静夫在研究自然数时发现了一个奇怪现象:对于任意一个自然数 n ,若 n 为偶数,则将其除以 2 ;若 n 为奇数,则将其乘以 3 ,然后再加 1 。如此经过有限次运算后,总可以得到自然数 1 。人们把谷角静夫的这一发现叫做“谷角猜想”。
要求:编写一个程序,由键盘输入一个自然数 n ,把 n 经过有限次运算后,最终变成自然数 1 的全过程打印出来。
(1)编程思路
定义迭代变量为n,按照谷角猜想的内容,可以得到两种情况下的迭代关系式:当 n 为偶数时,n=n/2 ;当 n 为奇数时, n=n*3+1 。
这就是需要计算机重复执行的迭代过程。这个迭代过程需要重复执行多少次,才能使迭代变量 n 最终变成自然数 1 ,这是我们无法计算出来的。因此,还需进一步确定用来结束迭代过程的条件。由于对任意给定的一个自然数 n ,只要经过有限次运算后,能够得到自然数 1 ,从而完成验证工作。因此,用来结束迭代过程的条件可以定义为: n==1 。
(2)源程序
#include <iostream>
using namespace std;
int main()
{
unsigned int data;
cout<<"请输入一个自然数:";
cin>>data;
while(data!=1)
{
if((data%2==0))
{
cout<<data<<"/2=";
data/=2;
cout<<data<<endl;
}
else
{
cout<<data<<"*3+1=";
data=data*3+1;
cout<<data<<endl;
}
}
return 0;
}
【例2】求平方根
用迭代法求某个数的平方根。已知求平方根的迭代公式为:
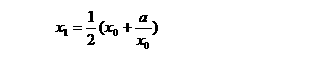
(1)编程思路
用迭代法求某个数a的平方根的算法为:
(1)先自定一个初值x0,作为a的平方根值,例如,取a/2作为x0的初值。利用迭代公式求出一个x1。此值与真正的a的平方根值相比,误差可能很大。
(2)把新求得的x1代入x0中,准备用此新的x0再去求出一个新的x1。
(3)利用迭代公式再求出一个新的x1的值,也就是用新的x0又求出一个新的平方根值x1,此值将更趋近于真正的平方根值。
(4)比较前后两次求得的平方根值x0和x1,如果它们的差值小于指定的值(如0.000001),即达到要求的精度,则认为x1就是a的平方根值,执行步骤5;否则执行步骤2,即循环进行迭代。
(5)迭代结束,输出结果x1。
(2) 源程序
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
double x0,x1,a ;
cin>>a;
x0 =a/2; // 迭代初值
x1 =0.5*(x0 + a/x0);
do
{
x0 = x1; // 为下一次迭代作准备
x1 = 0.5*(x0 + a/x0);
} while (fabs(x1-x0)>0.000001);
cout<<x1<<endl; // 输出结果
return 0 ;
}