参考自:https://www.cnblogs.com/ECJTUACM-873284962/p/6423483.html
B. Code For 1
Jon fought bravely to rescue the wildlings who were attacked by the white-walkers at Hardhome. On his arrival, Sam tells him that he wants to go to Oldtown to train at the Citadel to become a maester, so he can return and take the deceased Aemon's place as maester of Castle Black. Jon agrees to Sam's proposal and Sam sets off his journey to the Citadel. However becoming a trainee at the Citadel is not a cakewalk and hence the maesters at the Citadel gave Sam a problem to test his eligibility.
Initially Sam has a list with a single element n. Then he has to perform certain operations on this list. In each operation Sam must remove any element x, such that x > 1, from the list and insert at the same position  ,
, 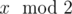 ,
,  sequentially. He must continue with these operations until all the elements in the list are either 0 or 1.
sequentially. He must continue with these operations until all the elements in the list are either 0 or 1.
Now the masters want the total number of 1s in the range l to r (1-indexed). Sam wants to become a maester but unfortunately he cannot solve this problem. Can you help Sam to pass the eligibility test?
The first line contains three integers n, l, r (0 ≤ n < 250, 0 ≤ r - l ≤ 105, r ≥ 1, l ≥ 1) – initial element and the range l to r.
It is guaranteed that r is not greater than the length of the final list.
Output the total number of 1s in the range l to r in the final sequence.
Examples
Input
7 2 5
Output
4
Input
10 3 10
Output
5
Note
Consider first example:

Elements on positions from 2-nd to 5-th in list is [1, 1, 1, 1]. The number of ones is 4.
For the second example:

Elements on positions from 3-rd to 10-th in list is [1, 1, 1, 0, 1, 0, 1, 0]. The number of ones is 5.
思路:
给你一个数n和区间(l,r),每次都能把任意数拆成 n/2,n%2,n/2 三个数,直到变成0和1,问区间l,r里有多少个1?
如 7 2 5
7 → 3 1 3;
3 → 1 1 1;
所以能拆成 7个 1,所以在2--5之间数字1的个数为4。
同理 10 3 10
10 → 5 0 5;
5 → 2 1 2;
2 → 1 0 1;
故拆成 → [ 1 0 1 1 1 0 1 0 1 0 1 1 1 0 1 ]
3--10之间数字1的个数为5.
解法: 分治的思想,二分法
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 ll n, l, r, s = 1, ans; 5 void solve(ll a, ll b, ll l, ll r, ll d){//二分的思想 6 if ( a > b || l > r ) return; 7 else{ 8 ll mid = (a+b)/2; 9 if ( r < mid )solve(a,mid-1,l,r,d/2); 10 else if ( mid < l )solve(mid+1,b,l,r,d/2); 11 else { 12 ans += d%2; 13 solve(a,mid-1,l,mid-1,d/2); 14 solve(mid+1,b,mid+1,r,d/2); 15 } 16 } 17 } 18 int main(){ 19 cin >> n >> l >> r; 20 ll p = n; 21 while ( p >= 2 ){ 22 p /= 2; 23 s = s*2+1; 24 } 25 solve(1,s,l,r,n); 26 cout << ans << endl; 27 return 0; 28 }