写在前面
阅读本文,请务必动手写代码测试,否则无法愉快玩耍。
如果你还不懂怎么开始编写一个MetaHook插件,请首先去看使用 MetaHook Plus 绘制 HUD来增加姿势。
这篇文章假设你已经有最最基础的以下技能:
- 编译和安装MetaHook
- 编译和安装MetaHook插件
- 最低程度地会写一丢丢C++代码
- 拥有初中或以上的姿势水平
正文开始
我们的游戏世界基于一个三维直角坐标系,如下图:
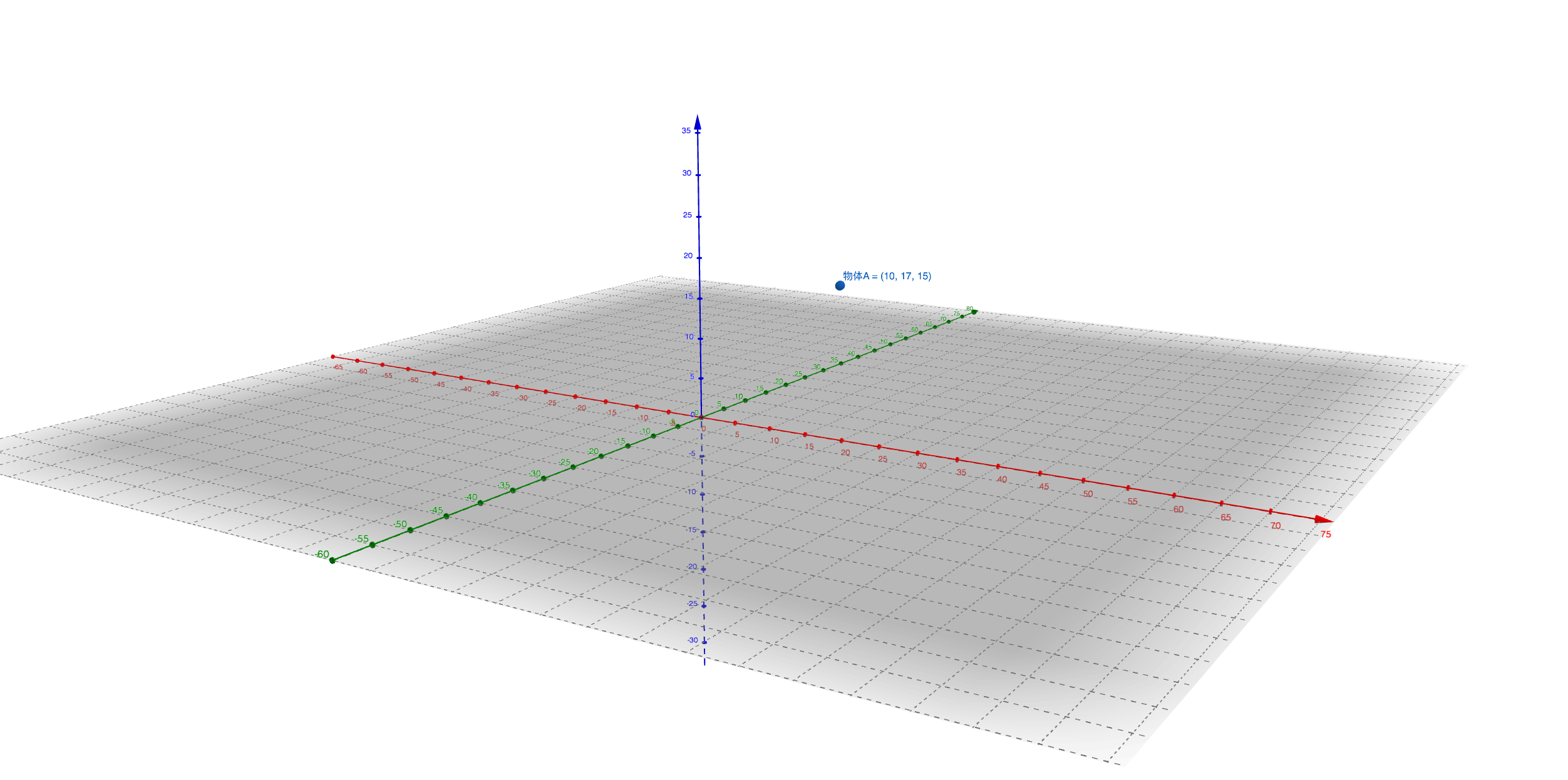
电脑端可以右键新标签页打开大图,手机端可以保存后查看大图。
在HL引擎中,X轴和Y轴组成的平面就是地面,当你在游戏中前后左右移动,你的X轴和Y轴的坐标值将会发生变化。当你往高处和低处移动时,Z轴的坐标值将会发生变化。所以可知:XY轴=前后左右 Z轴=上下
我们可以编写代码在游戏中实时输出坐标值来观察:
int HUD_Redraw(float time, int intermission) { cl_entity_t* local = gEngfuncs.GetLocalPlayer(); gEngfuncs.Con_Printf("position=(%f,%f,%f) ", local->curstate.origin[0], local->curstate.origin[1], local->curstate.origin[2]); return gExportfuncs.HUD_Redraw(time, intermission); }
使用 -dev 参数启动游戏,进入游戏后,在屏幕左上角将会看到输出的坐标值。
很显然,我们要实现小地图,只需要XY这两个轴就行了,所以我们不妨先作个图:
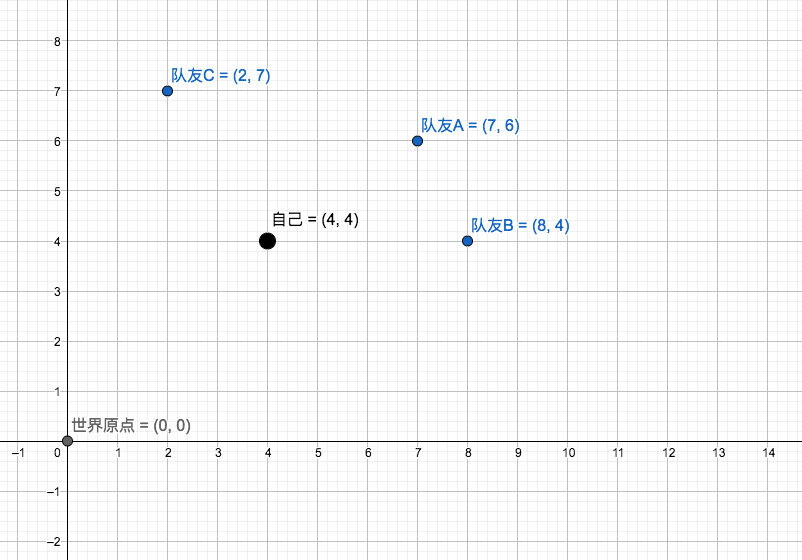
我们可以编写代码获取一些实体的坐标试试看:
int HUD_Redraw(float time, int intermission) { // 索引1到32都是玩家 for (int i = 1; i <= 32; i++) { // 根据索引获取实体 cl_entity_t* entity = gEngfuncs.GetEntityByIndex(i); if (!entity || !entity->model) continue; // 取得实体的XY坐标,通常来说三维坐标值都比较大,所以我们乘以0.2,也就是缩小到20% vec2_t position; position[0] = (int)(entity->curstate.origin[0] * 0.2); position[1] = (int)(entity->curstate.origin[1] * 0.2); // 在HUD上绘制小方块 gEngfuncs.pfnFillRGBA(position[0], position[1], 8, 8, 255, 255, 255, 255); } return gExportfuncs.HUD_Redraw(time, intermission); }
然后进入 cs_italy 这个地图的匪徒出生点,加几个BOT,并且把它们暂停,你就可以在HUD上看到最简陋的 小地图 了,如下:
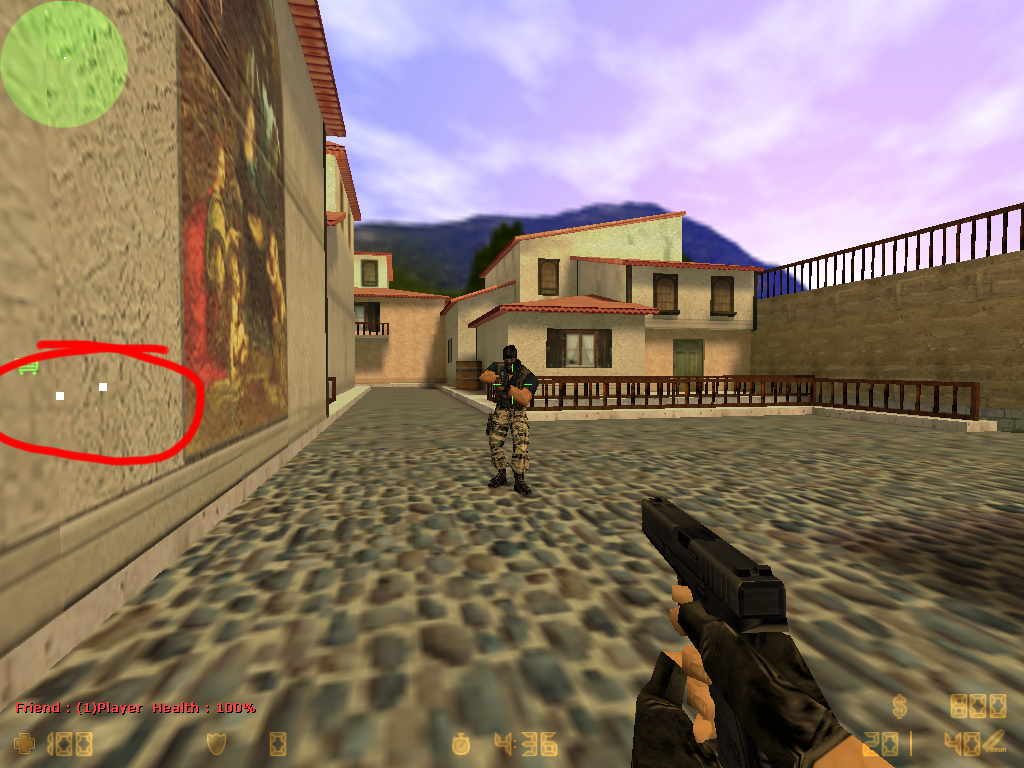
此时如果你移动位置,白色小方块也会跟着移动。
你会发现,稍微走走,小方块就跑到屏幕外面去了。很显然,我们需要以自己为中心,来显示其它人的位置。
相对坐标
回顾上面的平面坐标系图,假如我们要以自己为中心,那就需要知道队友“在哪”。
自己的坐标是(4,4),队友A的坐标是(7,6)
如果要以自己为中心,自己的坐标就是(0,0),那么此时队友A的坐标是多少呢?
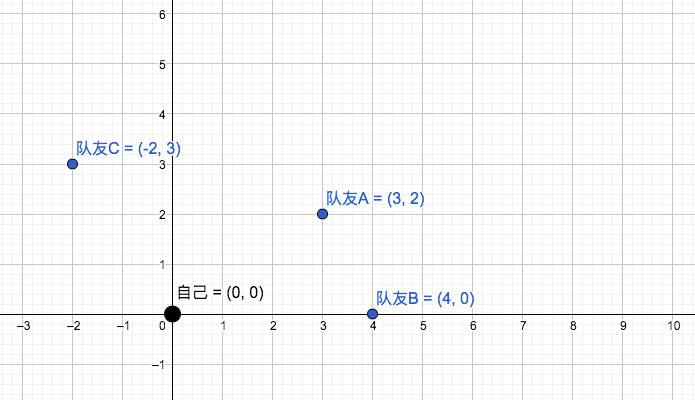
你可以看到队友A的坐标为(3,2),那这个坐标是怎么算出来的呢?
其实就是减法而已,如下:
(7,6)-(4,4)=(3,2)
很好,我们现在已经知道相对于自己来说队友“在哪”了,现在我们在HUD上取一点,用来显示自己的位置。
int HUD_Redraw(float time, int intermission) { cl_entity_t* local = gEngfuncs.GetLocalPlayer(); // 在HUD上取一点,显示自己的位置 const vec2_t hudPos = { 300, 300 }; // 绘制自己的方块(红色) gEngfuncs.pfnFillRGBA(hudPos[0], hudPos[1], 8, 8, 255, 0, 0, 255); // 自己的坐标,通常来说三维坐标值都比较大,所以我们乘以0.2,也就是缩小到20% vec2_t selfPos; selfPos[0] = (int)(local->curstate.origin[0] * 0.2); selfPos[1] = (int)(local->curstate.origin[1] * 0.2); // 索引1到32都是玩家 for (int i = 1; i <= 32; i++) { // 根据索引获取实体 cl_entity_t* entity = gEngfuncs.GetEntityByIndex(i); if (!entity || !entity->model) continue; // 自己不用画 if (entity == local) continue; // 取得实体的坐标,为了和selfPos单位统一,也要缩放20% vec2_t entPos; entPos[0] = (int)(entity->curstate.origin[0] * 0.2); entPos[1] = (int)(entity->curstate.origin[1] * 0.2); // 算出队友相对于自己的坐标 vec2_t offset; offset[0] = entPos[0] - selfPos[0]; offset[1] = entPos[1] - selfPos[1]; // 绘制队友小方块(白色) // 自己的坐标 + 相对的队友坐标 = 以自己为中心时队友的坐标 gEngfuncs.pfnFillRGBA(hudPos[0] + offset[0], hudPos[1] + offset[1], 8, 8, 255, 255, 255, 255); } return gExportfuncs.HUD_Redraw(time, intermission); }
效果如下:
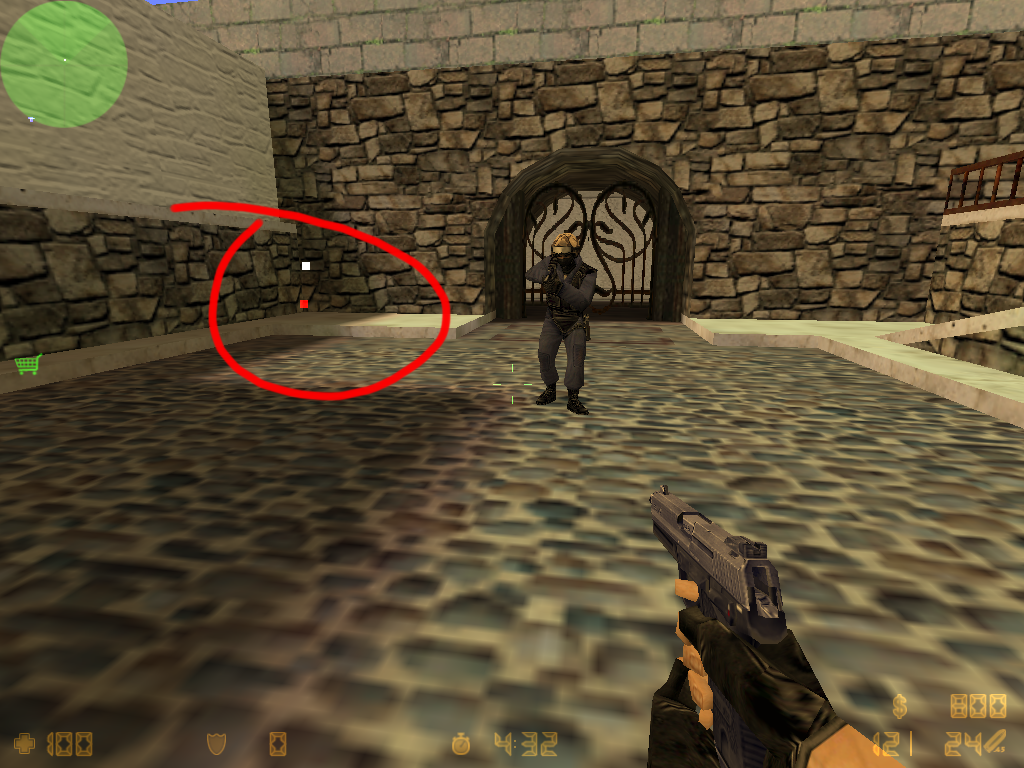
此时无论在地图何处,自己的位置(红色小方块)始终显示在HUD上(300,300)的位置,此时相对的队友的位置(白色小方块)位置也正确。
方向
在上面的例子中,你会发现无论在游戏中朝向哪里看,白色小方块相对于红色小方块的方向都没有任何改变。
而我们想要的效果是:自己前方的队友应该显示在红色小方块上面,自己后方的队友应该显示在小方块的下面。
首先我们要知道自己朝向哪个角度:
int HUD_Redraw(float time, int intermission) { cl_entity_t* local = gEngfuncs.GetLocalPlayer(); // angles使用欧拉角,详情可以搜索相关资料。 // 引擎的angles定义如下: // angles[0] = PITCH // angles[1] = YAW // angles[2] = ROLL // 我们只关心左右朝向,所以只看yaw gEngfuncs.Con_Printf("yaw=%f ", local->curstate.angles[1]); // ... }
相关资料:
https://blog.csdn.net/modestbean/article/details/79135769
假设你当前朝向YAW=0°,并且你的正前方有队友A,那么此时坐标系如下图:
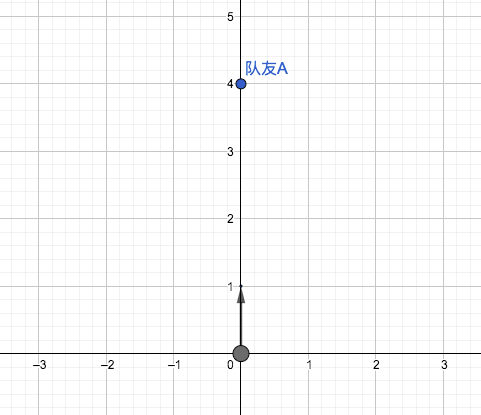
保持朝向YAW=0°让队友A站在你正前方,白色小方块(队友A)应该在红色小方块上面。为了确认这件事,我们要运行测试代码看看:
int HUD_Redraw(float time, int intermission) { cl_entity_t* local = gEngfuncs.GetLocalPlayer(); float yaw = local->curstate.angles[1]; // 引擎里YAW值的范围是-180~180,我们可以转换为0~360,小于0时加上360即可 if (yaw < 0) yaw += 360; // 在HUD上取一点,显示自己的位置 const vec2_t hudPos = { 300, 300 }; // 绘制自己的方块(红色) gEngfuncs.pfnFillRGBA(hudPos[0], hudPos[1], 8, 8, 255, 0, 0, 255); // 自己的坐标,通常来说三维坐标值都比较大,所以我们乘以0.2,也就是缩小到20% vec2_t selfPos; selfPos[0] = (int)(local->curstate.origin[0] * 0.2); selfPos[1] = (int)(local->curstate.origin[1] * 0.2); // 索引1到32都是玩家 for (int i = 1; i <= 32; i++) { // 根据索引获取实体 cl_entity_t* entity = gEngfuncs.GetEntityByIndex(i); if (!entity || !entity->model) continue; // 自己不用画 if (entity == local) continue; // 取得队友实体的坐标,为了和selfPos单位统一,也要缩放20% vec2_t entPos; entPos[0] = (int)(entity->curstate.origin[0] * 0.2); entPos[1] = (int)(entity->curstate.origin[1] * 0.2); // 算出队友相对于自己的坐标 vec2_t diffPos; diffPos[0] = entPos[0] - selfPos[0]; diffPos[1] = entPos[1] - selfPos[1]; gEngfuncs.Con_Printf("yaw=%f red=(%f,%f) white=(%f,%f) ", yaw, 0.0, 0.0, diffPos[0], diffPos[1]); // 绘制队友小方块(白色) gEngfuncs.pfnFillRGBA(hudPos[0]+diffPos[0], hudPos[1]+diffPos[1], 8, 8, 255, 255, 255, 255); } return gExportfuncs.HUD_Redraw(time, intermission); }
运行结果如下:
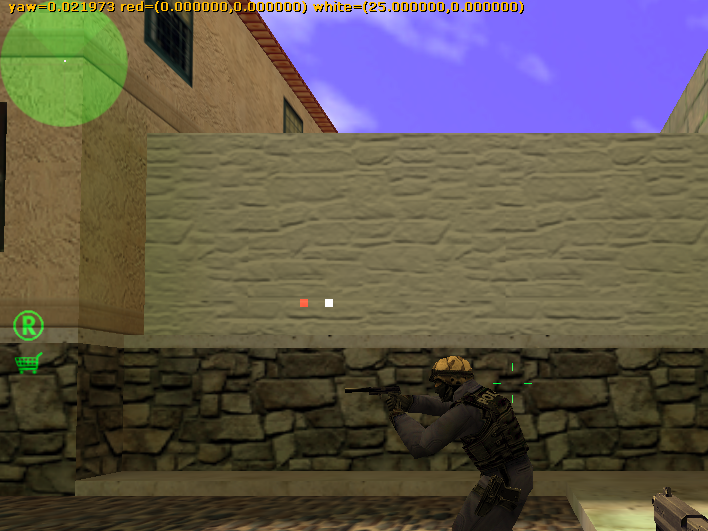
YAW=0°
红色小方块坐标为(0,0)即以自己为中心。
白色小方块坐标为(25,0)。
跟预想中的效果不一样。在游戏中,我已经使YAW=0°,并且队友站在正前方。此时白色小方块应该在红色小方块上面,而它现在在右边。
观察白色小方块的坐标值,可以发现它X轴值比红色小方块的大了25。
这说明三维坐标系里的XY轴并不能直接对应HUD二维坐标系的XY轴,我们需要做一点转换。
为了让白色小方块在红色小方块上面,我们需要交换白色小方块的XY轴。
交换之后白色小方块的坐标为(0,25)。
它的X轴已经和红色小方块的X轴对应,都是0。
而它的Y轴却比红色小方块的Y轴大了25,也就是说它会在红色小方块的下面,而我们想让他在红色小方块上面。只需要把Y轴取反就行。
实际上,X轴也要取反。
代码如下:
// 算出队友相对于自己的坐标 vec2_t diffPos; diffPos[0] = entPos[0] - selfPos[0]; diffPos[1] = entPos[1] - selfPos[1]; // 转换坐标轴 vec2_t finalPos; finalPos[0] = diffPos[1]; finalPos[1] = diffPos[0]; finalPos[1] = -finalPos[1]; // 绘制队友小方块(白色) gEngfuncs.pfnFillRGBA(hudPos[0] + finalPos[0], hudPos[1] + finalPos[1], 8, 8, 255, 255, 255, 255);
尝试前后左右走动,确定白色小方块的坐标已经正确,如图:

方向(二)
当你在游戏中稍微往右边看,假设你向右旋转了30°,小地图上的队友A的小方块应该要稍微往左边移动,如下图:
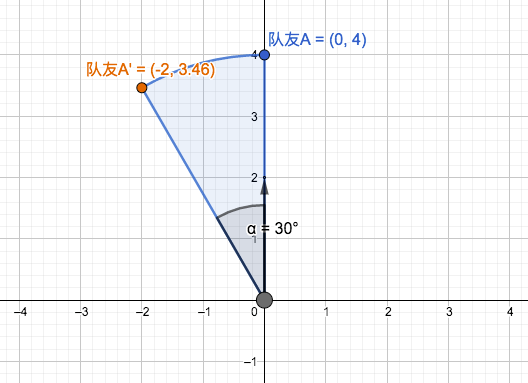
也就是说,我们必须把队友A的小方块逆时针旋转30°,这样看起来才会正确。
为了计算旋转后的坐标,我们需要一个函数,如下:
#define _USE_MATH_DEFINES #include <math.h> //---------- // in - 要旋转的点 // o - 圆心点 // angle - 旋转角度(单位为弧度,正为顺时针,负为逆时针) // out - 旋转后的点 //---------- void RotateByPoint(const vec2_t in, const vec2_t o, float angle, vec2_t out) { float ca = cos(angle); float sa = sin(angle); out[0] = (in[0] - o[0])*ca - (in[1] - o[1])*sa + o[0]; out[1] = (in[0] - o[0])*sa + (in[1] - o[1])*ca + o[1]; }
这个函数计算出二维坐标系中一个点绕另一个点旋转指定角度后的新坐标。
那么现在开始写旋转的代码:
// 转换坐标轴 vec2_t finalPos; finalPos[0] = diffPos[1]; finalPos[1] = diffPos[0]; finalPos[1] = -finalPos[1]; // 计算旋转 float angle = yaw * (M_PI / 180.0); // 角度转弧度 vec2_t o = { 0, 0 }; // 圆心点 vec2_t out; // 旋转后的点 RotateByPoint(finalPos, o, angle, out); // 绘制队友小方块(白色) gEngfuncs.pfnFillRGBA(hudPos[0]+ out[0], hudPos[1]+ out[1], 8, 8, 255, 255, 255, 255);
因为引擎的设定是:往右手边转,YAW就会减小。往左手边转,YAW就变大。
而RotateByPoint函数规定:angle值小了就逆时针转,大了就顺时针转,所以越往右手边转,YAW值就越小,就越往逆时针方向转。这刚好符合我们的需求,不用取反了。
所以我们直接传yaw进去就行了。因为RotateByPoint函数要求angle的单位必须是弧度,所以我们先要把yaw的单位转换为弧度。
运行结果如下:
尝试往右看,白色小方块就往另外一边走了,一切顺利 。
所以我们先把完整的代码贴一下:
#include <metahook.h> cl_enginefunc_t gEngfuncs; int Initialize(struct cl_enginefuncs_s *pEnginefuncs, int iVersion) { memcpy(&gEngfuncs, pEnginefuncs, sizeof(gEngfuncs)); return gExportfuncs.Initialize(pEnginefuncs, iVersion); } void HUD_Init(void) { return gExportfuncs.HUD_Init(); } #define _USE_MATH_DEFINES #include <math.h> //---------- // in - 要旋转的点 // o - 圆心点 // angle - 旋转角度(单位为弧度,正为顺时针,负为逆时针) // out - 旋转后的点 //---------- void RotateByPoint(const vec2_t in, const vec2_t o, float angle, vec2_t out) { float ca = cos(angle); float sa = sin(angle); out[0] = (in[0] - o[0])*ca - (in[1] - o[1])*sa + o[0]; out[1] = (in[0] - o[0])*sa + (in[1] - o[1])*ca + o[1]; } int HUD_Redraw(float time, int intermission) { cl_entity_t* local = gEngfuncs.GetLocalPlayer(); float yaw = local->curstate.angles[1]; // 引擎里YAW值的范围是-180~180,我们可以转换为0~360,小于0时加上360即可 if (yaw < 0) yaw += 360; // 在HUD上取一点,显示自己的位置 const vec2_t hudPos = { 300, 300 }; // 绘制自己的方块(红色) gEngfuncs.pfnFillRGBA(hudPos[0], hudPos[1], 8, 8, 255, 0, 0, 255); // 自己的坐标,通常来说三维坐标值都比较大,所以我们乘以0.2,也就是缩小到20% vec2_t selfPos; selfPos[0] = (int)(local->curstate.origin[0] * 0.2); selfPos[1] = (int)(local->curstate.origin[1] * 0.2); // 索引1到32都是玩家 for (int i = 1; i <= 32; i++) { // 根据索引获取实体 cl_entity_t* entity = gEngfuncs.GetEntityByIndex(i); if (!entity || !entity->model) continue; // 自己不用画 if (entity == local) continue; // 取得队友实体的坐标,为了和selfPos单位统一,也要缩放20% vec2_t entPos; entPos[0] = (int)(entity->curstate.origin[0] * 0.2); entPos[1] = (int)(entity->curstate.origin[1] * 0.2); // 算出队友相对于自己的坐标 vec2_t diffPos; diffPos[0] = entPos[0] - selfPos[0]; diffPos[1] = entPos[1] - selfPos[1]; // 转换坐标轴 vec2_t finalPos; finalPos[0] = diffPos[1]; finalPos[1] = diffPos[0]; finalPos[1] = -finalPos[1]; // 计算旋转 float angle = yaw * (M_PI / 180.0); // 角度转弧度 vec2_t o = { 0, 0 }; // 圆心点 vec2_t out; // 旋转后的点 RotateByPoint(finalPos, o, angle, out); // 绘制队友小方块(白色) gEngfuncs.pfnFillRGBA(hudPos[0]+ out[0], hudPos[1]+ out[1], 8, 8, 255, 255, 255, 255); } return gExportfuncs.HUD_Redraw(time, intermission); }
调整
经过以上的操作,就已经完成了一个最简单的雷达:
- 以自己为中心
- 其它人相对自己的位置正确
- 其它人相对自己的方向正确
你可以继续修改上面的代码,让你的雷达(1.0)变得更好看一些。