heap(堆)并不是STL的容器组件,是priority queue(优先队列)的底层实现机制,因为binary max heap(大根堆)总是最大值位于堆的根部,优先级最高。
binary heap本质是一种complete binary tree(完全二叉树),整棵binary tree除了最底层的叶节点之外,都 是填满的,但是叶节点从左到右不会出现空隙,如下图所示就是一颗完全二叉树
完全二叉树内没有任何节点漏洞,是非常紧凑的,这样的一个好处是可以使用array来存储所有的节点, 因为当其中某个节点位于$i$处,其左节点必定位于$2i$处,右节点位于$2i+1$处,父节点位于$i/2$(向 下取整)处。这种以array表示tree的方式称为隐式表述法。
因此我们可以使用一个array和一组heap算法来实现max heap(每个节点的值大于等于其子节点的值)和 min heap(每个节点的值小于等于其子节点的值)。由于array不能动态的改变空间大小,用vector代替 array是一个不错的选择。
那heap算法有哪些?常见有的插入、弹出、排序和构造算法,下面一一进行描述。
push_heap插入算法
由于完全二叉树的性质,新插入的元素一定是位于树的最底层作为叶子节点,并填补由左至右的第一个 空格。事实上,在刚执行插入操作时,新元素位于底层vector的end()处,之后是一个称为percolate up(上溯)的过程,举个例子如下图:
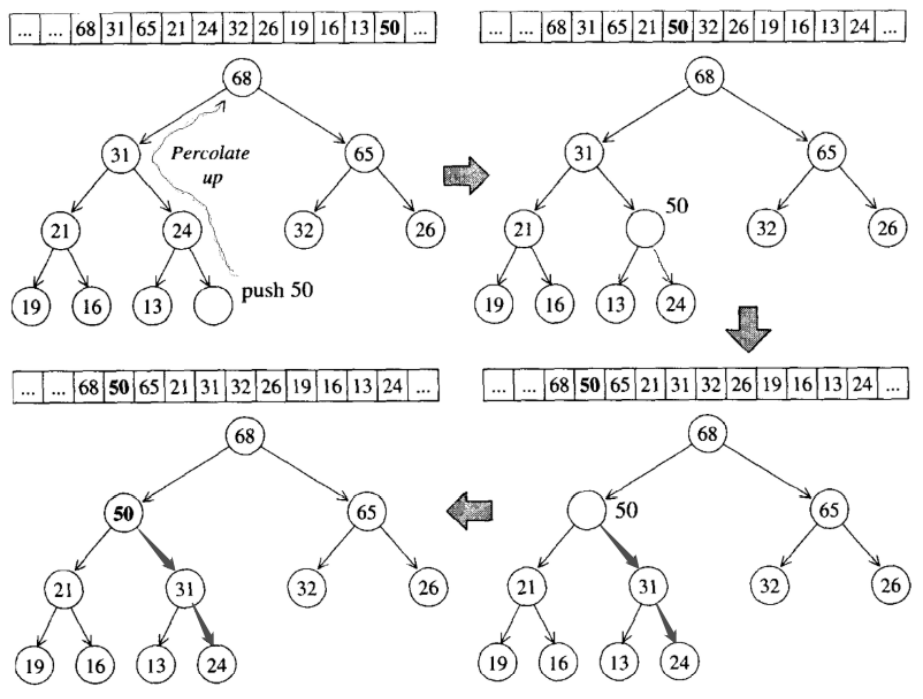
新元素50在插入堆中后,先放在vector的end()存着,之后执行上溯过程,调整其根结点的位置,以便满 足max heap的性质,如果了解大根堆的话,这个原理跟大根堆的调整过程是一样的。
pop_heap算法
heap的pop操作实际弹出的是根节点吗,但在heap内部执行pop_heap时,只是将其移动到vector的最后位 置,然后再为这个被挤走的元素找到一个合适的安放位置,使整颗树满足完全二叉树的条件。这个被挤 掉的元素首先会与根结点的两个子节点比较,并与较大的子节点更换位置,如此一直往下,直到这个被 挤掉的元素大于左右两个子节点,或者下放到叶节点为止,这个过程称为percolate down(下溯)。举个 例子:
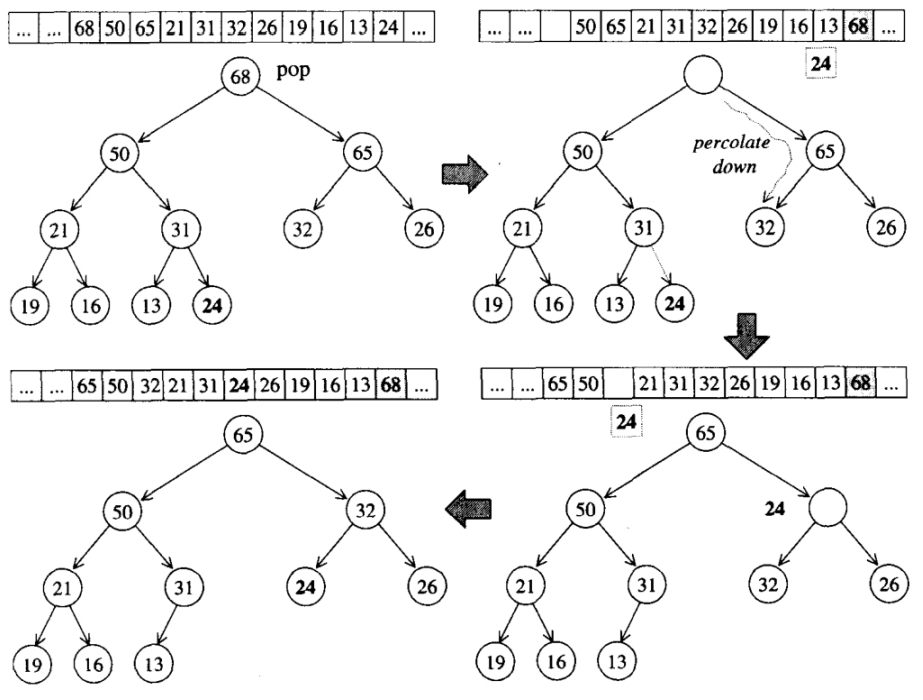
根节点68被pop之后,移到了vector的最底部,将24挤出,24被迫从根节点开始与其子节点进行比较,直 到找到合适的位置安身,需要注意的是pop之后元素并没有被移走,如果要将其移走,可以使用 pop_back()。
sort算法
一言以蔽之,因为pop_heap可以将当前heap中的最大值置于底层容器vector的末尾,heap范围减1,那么 不断的执行pop_heap直到树为空,即可得到一个递增序列。
make_heap算法
将一段数据转化为heap,一个一个数据插入,调用上面说的两种percolate算法即可。
代码实测:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main()
{
vector<int> v = { 0,1,2,3,4,5,6 };
make_heap(v.begin(), v.end()); //以vector为底层容器
for (auto i : v)
{
cout << i << " "; // 6 4 5 3 1 0 2
}
cout << endl;
v.push_back(7);
push_heap(v.begin(), v.end());
for (auto i : v)
{
cout << i << " "; // 7 6 5 4 1 0 2 3
}
cout << endl;
pop_heap(v.begin(), v.end());
for (auto i : v)
{
cout << i << " "; // 6 4 5 3 1 0 2 7
}
cout << endl;
cout << v.back() << endl; // 7
v.pop_back();
for (auto i : v)
{
cout << i << " "; // 6 4 5 3 1 0 2
}
cout << endl;
sort_heap(v.begin(), v.end());
for (auto i : v)
{
cout << i << " "; // 0 1 2 3 4 5 6
}
return 0;
}