数据结构

link

mean

给定n个数，按照构造Binary Search Tree的方式来构造BST树，按顺序输出每一个非root结点的父节点的值。

analyse

构造BST树最坏情况下时间复杂度为O(n)，肯定会超时。

注意到只需要输出结点的父节点的值，不需要真的构造BST树。

插到第i个结点时，我们在前i-1个结点中找两个数，一个是比Ai大的最小数，一个是比Ai小的最大数。

那么Ai的父节点肯定是这两个中的一个，到底是哪一个呢，根据画图分析，可以得出是后来插入的那个。

如下图所示：

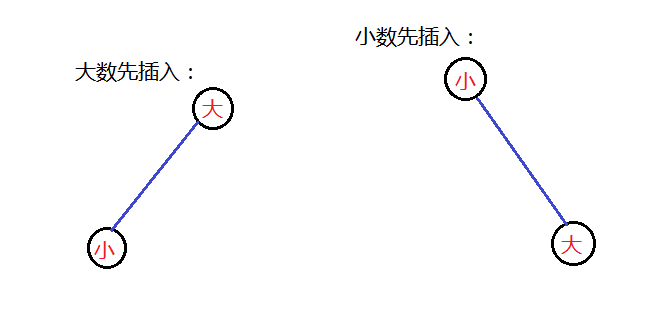
做法：用java里面的容器TreeMap<Integer,Integer>来存储<value,index>对，根据value值来查找，然后比较这两个数的index大小来判断谁是父节点。

time complexity

O(n*logn)

code

1. java容器实现 

import java.io.BufferedInputStream;
import java.util.HashMap;
import java.util.Scanner;
import java.util.TreeSet;

public class Main{
   public static void main(String[]argv){
       Scanner in=new Scanner(new BufferedInputStream(System.in));
       while(in.hasNext()){
           int n=in.nextInt();
           TreeSet<Integer> vals=new TreeSet<>();
           HashMap<Integer,Integer> idx=new HashMap<>();
           int val=in.nextInt();
           vals.add(val);
           idx.put(val,0);
           for(int i=1;i<n;++i){
               val=in.nextInt();
               Integer hi=vals.higher(val), lo=vals.lower(val);
               if(hi==null)
                   System.out.print(lo+" ");
               else if(lo==null)
                   System.out.print(hi+" ");
               else {
                   Integer hiIdx=idx.get(hi);
                   Integer loIdx=idx.get(lo);
                   if(hiIdx>loIdx)
                       System.out.print(hi+" ");
                   else
                       System.out.print(lo+" ");
               }
               vals.add(val);
               idx.put(val,i);
           }
           System.out.println();
       }
   }
}

2. avl实现 
#include<iostream>
 #include<cstdio>
 #include<set>
 #include<map>
 #include<vector>
 using namespace std;
 
 ;
 
 //AVL树节点信息
 class TreeNode
 {
 public:
     TreeNode() :lson(NULL), rson(NULL), freq(), hgt() {}
     int data;//值
     int hgt;//高度
     unsigned int freq;//频率
     TreeNode* lson;//指向左儿子的地址
     TreeNode* rson;//指向右儿子的地址
 };
 //AVL树类的属性和方法声明
 class AVLTree
 {
 private:
     TreeNode* root;//根节点
     void insertpri(TreeNode* &node,int x,int &pre,int &aft);//插入
     int height(TreeNode* node);//求树的高度
     void SingRotateLeft(TreeNode* &k2);//左左情况下的旋转
     void SingRotateRight(TreeNode* &k2);//右右情况下的旋转
     void DoubleRotateLR(TreeNode* &k3);//左右情况下的旋转
     void DoubleRotateRL(TreeNode* &k3);//右左情况下的旋转
     int Max(int cmpa, int cmpb);//求最大值
 public:
     AVLTree() :root(NULL) {}
     void insert(int x,int &pre,int &aft);//插入接口
 };
 //计算节点的高度
 int AVLTree::height(TreeNode* node)
 {
     if (node != NULL)
         return node->hgt;
     ;
 }
 //求最大值
 int AVLTree::Max(int cmpa, int cmpb)
 {
     return cmpa>cmpb ? cmpa : cmpb;
 }
 //左左情况下的旋转
 void AVLTree::SingRotateLeft(TreeNode* &k2)
 {
     TreeNode* k1;
     k1 = k2->lson;
     k2->lson = k1->rson;
     k1->rson = k2;
 
     k2->hgt = Max(height(k2->lson), height(k2->rson)) + ;
     k1->hgt = Max(height(k1->lson), k2->hgt) + ;
     k2 = k1;
 }
 //右右情况下的旋转
 void AVLTree::SingRotateRight(TreeNode* &k2)
 {
     TreeNode* k1;
     k1 = k2->rson;
     k2->rson = k1->lson;
     k1->lson = k2;
 
     k2->hgt = Max(height(k2->lson), height(k2->rson)) + ;
     k1->hgt = Max(height(k1->rson), k2->hgt) + ;
     k2 = k1;
 }
 //左右情况的旋转
 void AVLTree::DoubleRotateLR(TreeNode* &k3)
 {
     SingRotateRight(k3->lson);
     SingRotateLeft(k3);
 }
 //右左情况的旋转
 void AVLTree::DoubleRotateRL(TreeNode* &k3)
 {
     SingRotateLeft(k3->rson);
     SingRotateRight(k3);
 }
 //插入
 void AVLTree::insertpri(TreeNode* &node, int x,int &pre,int &aft)
 {
     if (node == NULL)//如果节点为空,就在此节点处加入x信息
     {
         node = new TreeNode();
         node->data = x;
         return;
     }
     if (node->data>x)//如果x小于节点的值,就继续在节点的左子树中插入x
     {
         aft = node->data;
         insertpri(node->lson, x,pre,aft);
          == height(node->lson) - height(node->rson))
             if (x<node->lson->data)
                 SingRotateLeft(node);
             else
                 DoubleRotateLR(node);
     }
     else if (node->data<x)//如果x大于节点的值,就继续在节点的右子树中插入x
     {
         pre = node->data;
         insertpri(node->rson, x,pre,aft);
          == height(node->rson) - height(node->lson))//如果高度之差为2的话就失去了平衡,需要旋转
             if (x>node->rson->data)
                 SingRotateRight(node);
             else
                 DoubleRotateRL(node);
     }
     else ++(node->freq);//如果相等,就把频率加1
     node->hgt = Max(height(node->lson), height(node->rson)) + ;
 }
 //插入接口
 void AVLTree::insert(int x,int &pre,int &aft)
 {
     insertpri(root, x,pre,aft);
 }
 
 map<int, int> lef, rig;
 
 int n;
 void init() {
     lef.clear(); rig.clear();
 }
 
 int main() {
     int v,pre,aft;
      && n) {
         AVLTree tree;
         init();
         scanf("%d", &v);
         tree.insert(v, pre, aft);
         vector<int> ans;
         ; i < n - ; i++) {
             scanf("%d", &v);
             pre = , aft = INF;
             tree.insert(v, pre, aft);
             //printf("pre:%d,aft:%d
", pre, aft);
             ) {
                 ans.push_back(aft);
                 lef[aft] = ;
             }
             else {
                 ans.push_back(pre);
                 rig[pre] = ;
             }
         }
         ; i < ans.size() - ; i++) printf("%d ", ans[i]);
         printf(]);
     }
     ;
 }