数论

Funny scales 

Problem's Link

 ----------------------------------------------------------------------------

Mean: 

给定两个数n和x，有一个天平，初始时左盘为x，你需要从以下集合中选一些数字来放到两个盘中，使得两个盘相等（note:每个数字只能取一次）。

analyse:

即:

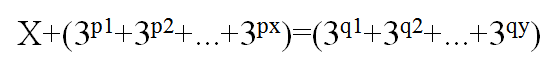
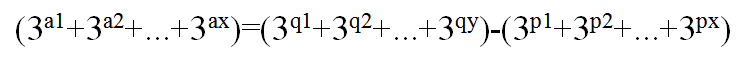
 将X化为3进制：

但是题目说每个3^i必须为1，所以我们需要将X表示成的等式的每一项的系数变为1，这就是本题的关键。

方法：

• 将X化为3进制的过程中，每一项的集合为{0,1,2} ，当遇到2时，将2表示成3-1的形式，即：向前进移位，本位置位-1。

如此一来便很好的处理了系数重复的问题，而且最后统计答案时，根据系数的符号来划分集合即可。

Time complexity: O(N)

 

view code

#include <cstdio>
const int MAXL = 100;

int N, X;
int A[MAXL], lenA;
int B[MAXL], lenB;
int dig[MAXL];

int main()
{

   scanf( "%d %d", &N, &X );

   for ( int i = 0; X != 0; i++ )
   {
       dig[i] += X % 3;
       if ( dig[i] > 1 )
       {
           dig[i + 1]++;
           dig[i] = dig[i] - 3;
       }
       X /= 3;
   }

   for ( int i = MAXL - 1; i >= 0; i-- )
   if ( dig[i] != 0 )
       if ( dig[i] == -1 )
           A[lenA++] = i + 1;
       else if ( dig[i] == +1 )
           B[lenB++] = i + 1;

   if ( A[0] > N || B[0] > N )
       printf( "-1 " );
   else
   {
       for ( int i = lenA - 1; i >= 0; i-- )
       printf( i ? "%d " : "%d", A[i] );
       printf( " " );
       for ( int i = lenB - 1; i >= 0; i-- )
       printf( i ? "%d " : "%d", B[i] );
       printf( " " );
   }
   return 0;
}