在光线追踪算法中, 光线与各类几何体求交, 是渲染着色的基础. 几何体根据表示方式不同可以分为两个大类:
- 隐式曲面, Implicit Surface. (隐含几何体的点信息)
- 显式曲面, Explicit Surface. (直接包含几何体的点线面信息)
几何体的隐式曲面和显式曲面表示形式, 区别有点类似于图形与图像的区别.
- 图形: 具有数学表达的几何对象 (点线面); 例如, 矢量图.
- 图像: 离散表达, 像素, 光栅化; 例如, 栅格图.
关于隐式曲面和显示曲面的详细介绍可以参考 [1]
Ray Equation
Ray, 光线, 定义为射线, 从一个点出发, 沿着某一方向前行.
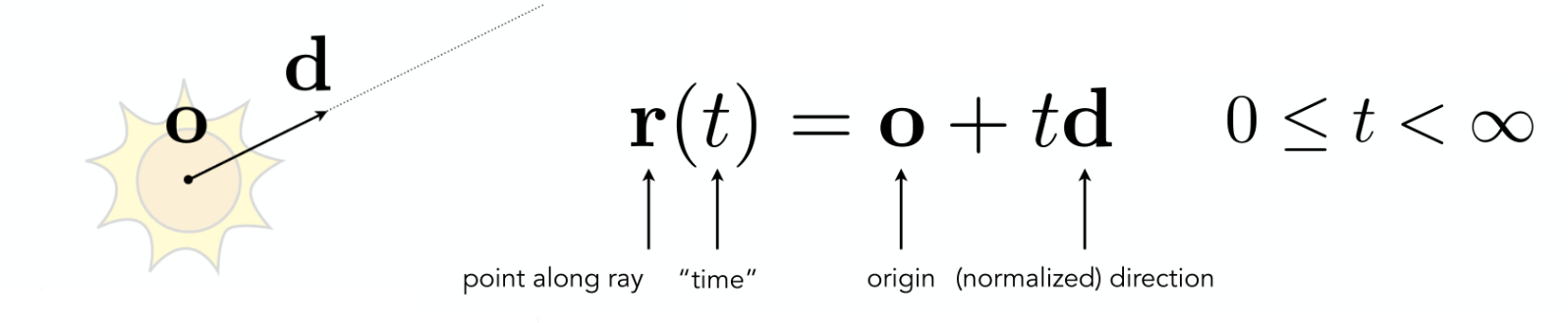
在 Ray 传播路径上的点 (P(x_p,y_p,z_p)), 都可以表示为以下形式:
(t) 的直观含义: 从光源出发, 沿着光线传播方向传播的距离/时间.
Implicit Surface
隐式曲面不会告诉任何点的信息, 只会告诉该曲面上所有点满足的关系.
三维空间中的隐式曲面可以统一表示为以下形式:
Ray 与曲面相交, 交点即在Ray上, 又在几何体上. 即:
只有一个变量 (t), 因此对于各种隐式曲面表达式, 结合各种数值方法 [2], 总能找到一个合适的解.
Sphere
交点计算结果
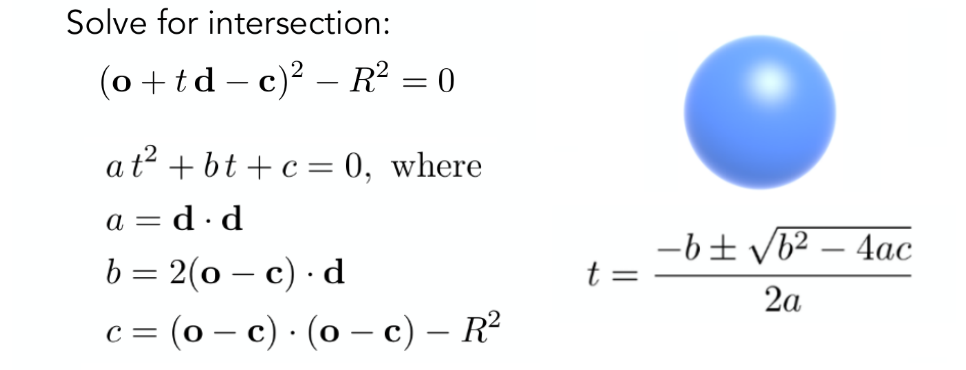
具体推导过程
对于简单几何体, 例如球, 我们可以推导交点与法线的坐标表示.
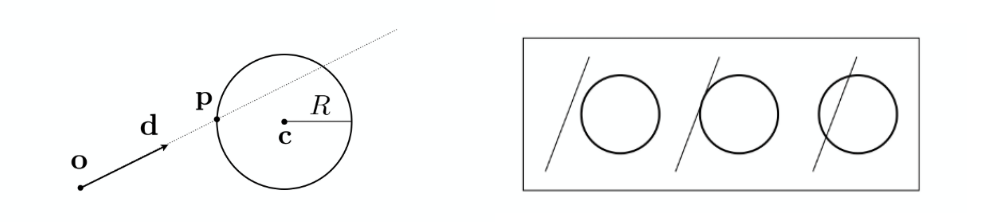
球的隐式曲面表示: 假设圆心为 (vec{c} = (c_x, c_y, c_z))
交点 (P(x_p,y_p,z_p)) 即在 Ray 上, 又在 Sphere 上, 满足:
此时未知量仅有 (t), 即:
(A, B, C) 的向量形式表示如下:
对于 (t) 为未知量的二元一次方程, 存在闭式解:
根据 (t) 的含义可知, (t) 的最小正数解对应于光线与物体最近的点 (P), 正数解的个数对应于球与光线的交点个数.
- 交点 (P = vec{o} + tvec{d});
- 法线 (vec{n} = vec{CP}), (圆心与交点的连线)
代码实现
auto x = ray.o - center;
double a = dot(ray.d, ray.d);
double b = 2 * dot(x, ray.d);
double c = dot(x, x) - radius * radius;
double t0, t1;
if (!Quadratic(a, b, c, &t0, &t1)) return false;
if (t0 > ray.tmax || t1 < 0.0) return false;
auto t = t0 < 0.0? t1: t0;
auto p_hit = ray.at(t);
auto p_norm = (p_hit - center).normalized();
Explicit Surface
Triangle Mesh, 三角网格, 由多个三角形组成, 是一类重要的隐式曲面. 三维物体常常组织为 Mesh 形式. 光线与三角形求交是光线与 Mesh 求交的基础.
Triangle Mesh
- 在不使用加速结构的情况下, 可以测试 Ray 与 Mesh 中的每一个三角形检测是否相交, 所有交点中最近的交点位置, 即是 Ray 与 Mesh 的交点.
- 当 Mesh 表示的物体有"内外"之分时: 奇数交点表示光源在 Mesh 内部; 偶数交点表示光源在物体外部. (不考虑相切)
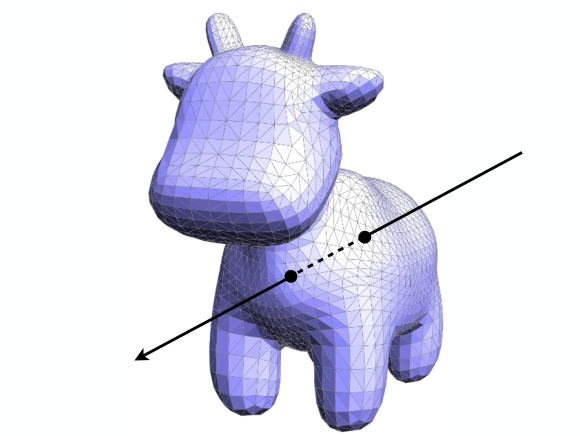
- 简单实现: 遍历每个三角形, 获取 Ray 与 Mesh 的交点.
bool TriMesh::intersect(const Ray &ray, double &t_hit, Interaction &isect) const {
bool hit = false;
for (auto triangle : triangles) {
if (triangle.get()->intersect(ray, t_hit, isect)) {
ray.tmax = t_hit;
hit = true;
}
}
return hit;
}
Triangle
有多种方法可以计算射线与三角形的交点, 比如高效的 Möller–Trumbore 算法[3]. 这里我们使用最直观的一种方式, 将射线与三角形求交分解为一下两个过程:
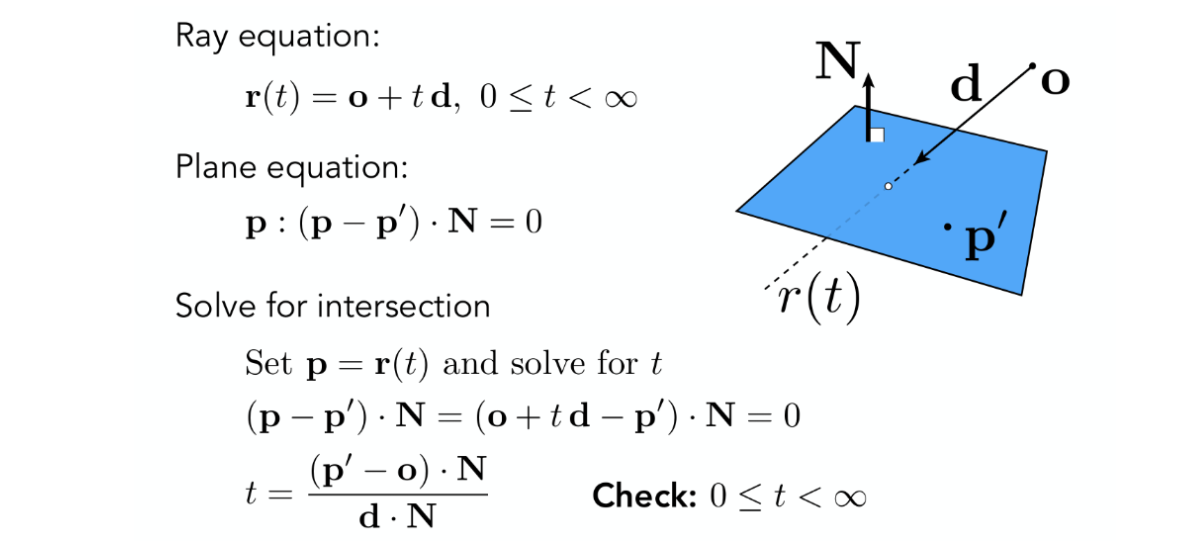
- 计算射线与三角形所在平面的交点
- 判断交点是否在三角形内部
交点计算结果
计算射线与三角形所在平面的交点计算;
判断交点是否在三角形内部 (叉乘判断) [4]
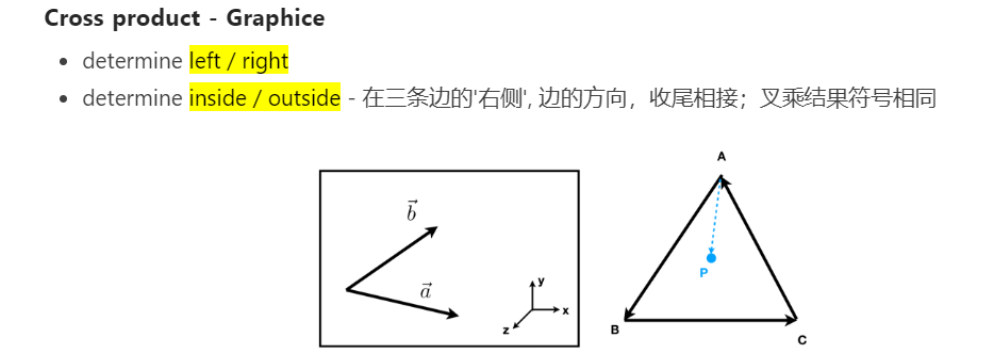
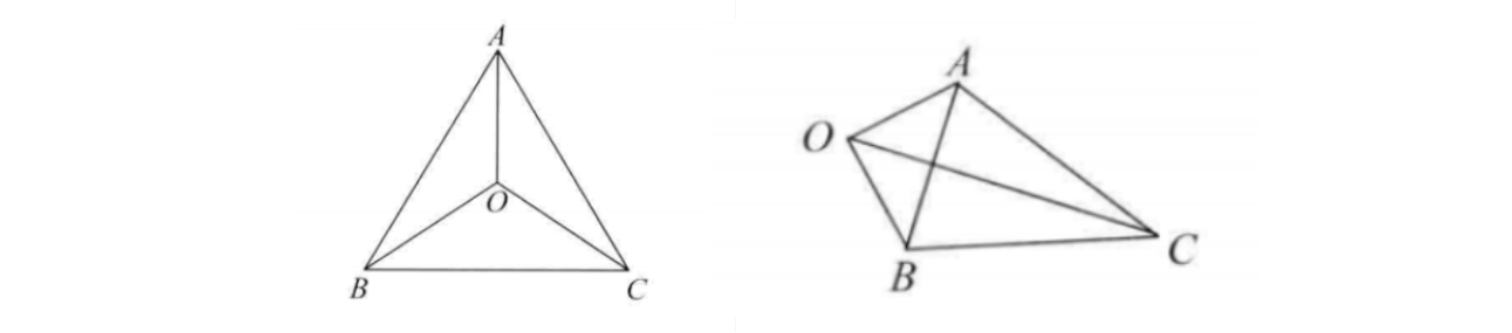
- 除了使用叉乘同向法, 还有内角和法[5], 面积法[6]等方法, 来计算判断一个点是否在三角形内部.
- 面积法: 当点在三角形内部时, 有 (S_{ riangle{ABC}} = S_{ riangle{OAB}}+S_{ riangle{OBC}}+S_{ riangle{OCA}}).
代码实现
// 1. Ray 与 三角形所在的平面相交, 得到交点 p
double t = dot((a - ray.o), n) / dot(ray.d, n);
if (t < 0 || t > ray.tmax) return false;
// 2. 判断交点 p 是否在三角形内部
auto p = ray.at(t);
auto ap = p - a;
auto bp = p - b;
auto cp = p - c;
auto t0 = cross(ab, ap);
auto t1 = cross(bc, bp);
auto t2 = cross(ca, cp);
auto ret_0 = dot(t0, t1);
auto ret_1 = dot(t1, t2);
auto ret_2 = dot(t2, t0);
// 3. 使用点乘判断叉乘结果是否同向
if (ret_0 < 0 || ret_1 < 0 || ret_2 < 0) return false;