数学
图论
最小树形图
问题直接顾名思义,略去。该问题常用朱刘算法,下面这张图很好地展示了它的流程,虽然确实丑得有点离谱了:
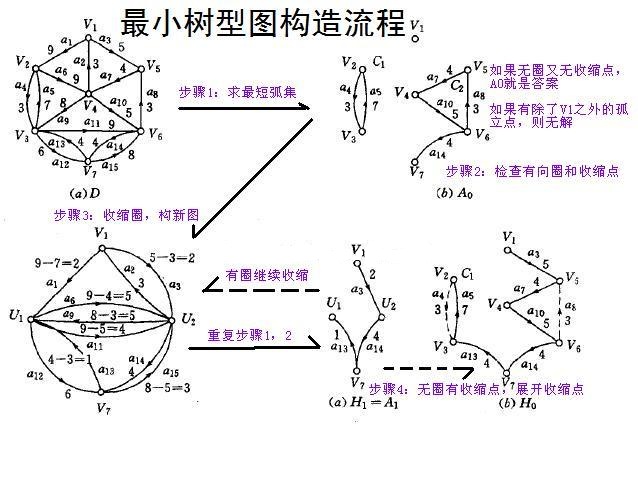
本质上朱刘算法就是一个反悔贪心:
- 初始,贪心选择最小入边。
- 没有出现环,我们必然找到了树形图。
- 覅原则,出现了环,我们必须要拆掉环上的一条边,这个过程通过修改环上所有点的入边边权(减去终点的最小边权)实现,这样在之后选中某条指向环的边的时候,我们就相当于用新边替换了旧边,使得树形图合法;可以发现这个过程一定会发生。
- 最后,收缩环,迭代。
以下是这个算法的 (O(|V||E|)) 实现:
int inE[MAXN], pre[MAXN], id[MAXN], vis[MAXN];
int fr[MAXM], to[MAXM], wei[MAXM];
int N, M; // N: 点数; M: 边数
LL ZhuLiu( int rt )
{
LL ret = 0;
int n = N, cnt = 0;
while( true )
{
cnt = 0;
rep( i, 1, n )
vis[i] = id[i] = 0, inE[i] = INF, pre[i] = -1;
rep( i, 1, M )
if( fr[i] ^ to[i] && wei[i] < inE[to[i]] )
inE[to[i]] = wei[i], pre[to[i]] = i;
// 寻找最小入边;注意我们必须忽略 " 自环 " ,因为这里的自环其实也有可能是缩环之前的环边。
rep( i, 1, n )
{
if( i == rt ) continue;
if( inE[i] == INF ) return -1;
else ret += inE[i];
}
rep( i, 1, n )
{
if( i == rt ) continue; int cur = i;
for( ; vis[cur] ^ i && ! id[cur] && cur ^ rt ; cur = fr[pre[cur]] ) vis[cur] = i;
if( ! id[cur] && cur ^ rt )
{
id[cur] = ++ cnt;
for( int u = fr[pre[cur]] ; u ^ cur ; u = fr[pre[u]] )
id[u] = cnt;
//注意我们可能并非一开始就在环上,而是走着走着掉进了一个环里
}
}
//找环,缩环
if( cnt == 0 ) break;
rep( i, 1, n ) if( ! id[i] ) id[i] = ++ cnt;
rep( i, 1, M )
{
int u = fr[i], v = to[i];
fr[i] = id[u], to[i] = id[v], wei[i] -= inE[v];
//保证忽略环边,因此可以对所有边进行修改
//对于不指向环的边,最小边权已经加入答案,且之后的最小边权必然为 0
}
// 修改边权,重新构图
rt = id[rt], n = cnt;
}
return ret;
}
朱刘算法还有其更加高效的实现。具体而言,我们考虑朱刘算法的过程:
- 对于一个点,找出最小入边
- 如果出现了环,合并环上的所有入边,接着回到 1
假如我们想用数据结构维护,不妨分析上述材料:
-
" 最小入边 " 体现了我们需要使用一种可以快速查询最小值的数据结构,堆应该是不错的选择。
-
" 环 " 说明了我们需要快速判断连通性,并查集可以很方便地解决。
-
" 合并入边 " 说明了我们需要一种可以快速合并的数据结构。
-
总之,我们可以使用可并堆维护每个点的出边集合,并查集判断连通性。
如果出现了环,我们就暴力把环上的出边收缩起来(总收缩次数是 (O(n)) 的)。在算法过程中我们需要始终维护连通性。
具体可以参考代码:
struct DSU
{
int fa[MAXN];
void MakeSet( const int siz ) { rep( i, 1, siz ) fa[i] = i; }
int FindSet( const int u ) { return fa[u] = ( fa[u] == u ? u : FindSet( fa[u] ) ); }
void UnionSet( const int u, const int v ) { fa[FindSet( u )] = FindSet( v ); }
}cir, link;
int fr[MAXM], to[MAXM];
int lch[MAXM], rch[MAXM], dist[MAXM], w[MAXM], tag[MAXM];
int rt[MAXN], pre[MAXN];
int N, M, R, ans = 0;
void Add( const int x, const int v ) { if( x ) w[x] += v, tag[x] += v; }
void Normalize( const int x ) { Add( lch[x], tag[x] ), Add( rch[x], tag[x] ), tag[x] = 0; }
int Merge( int u, int v )
{
if( ! u || ! v ) return u | v;
if( w[u] > w[v] ) swapp( u, v );
Normalize( u ); rch[u] = Merge( rch[u], v );
if( dist[lch[u]] < dist[rch[u]] ) swapp( lch[u], rch[u] );
dist[u] = dist[rch[u]] + 1; return u;
}
int Pop( const int u )
{
Normalize( u );
return Merge( lch[u], rch[u] );
}
bool Get( const int u )
{
for( ; cir.FindSet( fr[rt[u]] ) == cir.FindSet( u ) ;
rt[u] = Pop( rt[u] ) );
//类似于朴素朱刘,这里不能取到环内边
//一定注意 判连通性 和 判环内 需要两个并查集,因为在环的最后一条边连上之前环其实已经连通了
if( ! rt[u] ) return false;
ans += w[pre[u] = rt[u]]; return true;
}
int main()
{
rep( i, 1, M )
rt[to[i]] = Merge( rt[to[i]], i );
cir.MakeSet( N ), link.MakeSet( N );
rep( i, 1, N )
if( i ^ R ) //每个点可以顺序寻找入边
{
if( ! Get( i ) ) return puts( "-1" ), 0;
while( link.FindSet( fr[pre[i]] ) == link.FindSet( i ) )
//假如出现环,则需要缩环
{
Add( rt[i], - w[pre[i]] );
for( int u = cir.FindSet( fr[pre[i]] ) ; u ^ i ; u = cir.FindSet( fr[pre[u]] ) )
{
Add( rt[u], - w[pre[u]] );
rt[i] = Merge( rt[i], rt[u] );
cir.UnionSet( u, i );
}
//暴力打标记合并,利用环的并查集跳转
if( ! Get( i ) ) return puts( "-1" ), 0;
}
link.UnionSet( i, fr[pre[i]] );
}
write( ans ), putchar( '
' );
return 0;
}
一般图最大匹配
常用带花树算法。主要思想是处理一般图上特殊的奇环,通过 balabala (出题人这只鸽子决定期末考完了再补)从而将说明可以将奇环缩成一个点,然后就可以像二分图匹配一样直接跑增广路增广。
具体可以参考代码:
int q[MAXN], h, t;
int head[MAXN], fa[MAXN], pre[MAXN], match[MAXN], vis[MAXN], travel[MAXN];
int N, M, cnt, tims = 0;
int LCA( int u, int v )
{
u = fa[u], v = fa[v], tims ++;
for( ; travel[u] ^ tims ; u ^= v ^= u ^= v )
if( u ) travel[u] = tims, u = fa[pre[match[u]]];
return u;
}
void Blossom( int u, int v, int lca )
{
while( fa[u] ^ lca )
{
pre[u] = v, v = match[u];
if( vis[v] == 1 ) vis[v] = 2, q[++ t] = v;
fa[u] = fa[v] = lca, u = pre[v];
}
}
bool Augment( const int sta )
{
int u, v; h = 1, t = 0;
rep( i, 1, N ) fa[i] = i, pre[i] = vis[i] = 0;
vis[q[++ t] = sta] = 2;
while( h <= t )
{
u = q[h ++];
for( int i = head[u] ; i ; i = Graph[i].nxt )
if( ! vis[v = Graph[i].to] )
{
vis[v] = 1, pre[v] = u;
if( ! match[v] )
for( int cur = v ; ; )
{
int nxt = match[pre[cur]];
match[cur] = pre[cur], match[pre[cur]] = cur;
if( pre[cur] == sta ) return true;
cur = nxt;
}
else vis[q[++ t] = match[v]] = 2;
}
else if( vis[v] == 2 && fa[u] ^ fa[v] )
{
int lca = LCA( u, v );
Blossom( u, v, lca ), Blossom( v, u, lca );
}
}
return false;
}
int main()
{
int ans = 0;
rep( i, 1, N )
ans += ! match[i] && Augment( i );
}
数据结构
字符串
其他
模拟退火
具体实现细节就不写了,提醒几点在下面:
- 退火其实还是类似于爬山,只不过是增加了跳出的概率。因此一次退火的过程中需要使用过程解进行迭代,如果用最优解迭代其实是没啥用的。
- 概率函数: (e^{frac{Delta}{T}}) ,注意 (Delta) 的正负。个人认为一个简单的判别方法是:作为一个概率值,函数值应该落在 ([0,1]) 里面,所以应该有 (Delta<0) 。
- 生成的新解需要在当前解的周围搜出一个点,注意新解的范围不要太小。
- 毕竟是个概率算法,正式场合少用,
除非你很会调参。