[互测题目]大括号树

题目

大意如下：

本题中的定义基于 [CSP2019]括号树 。

给定一棵树，树上节点有对应字符，均为 ( 或 )。

定义 (ans(P,Q)) 表示从 (P) 到 (Q) 的简单路径上的字符（包含两端）组成的字符串中，合法的子串的数量。

请你求出：

[sum_{P=1}^nsum_{Q=1}^n ans(P,Q)mod 998244353 ]

其中 (nle 2 imes 10^5) 。

分析

首先发现一个很显然的东西：问题的答案等价于求：

[sum_{S}cnt(S)=sum_{(u,v) ext{ is legal}} siz(u) imes siz(v) ]

即所有合法路径的出现次数之和，而这个东西又可以转化为路径两端子树大小之积。

既然是统计路径，那么自然就该树分治出场了。由于权在点上，这里我选用边分治。

写过之后你就会发现 dsu on tree 的确是很香的算法

每条路径的贡献在分治过程中很好维护吗，关键是解决路径判断合法的问题。

考虑一个经典括号问题的转化：将(看作 (+1) ，)看作 (-1) 。那么原先一条路径就可以被量化为一个值。

此时我们就可以定义 (f(u)) 为 (u) 到分治边的路径的值，(f(S)) 为字符串 (S) 的权值。

再思考一下经过分治边的路径的模样：分治边的一侧有多余的左括号，且没有失配的右括号，另一侧有多余的右括号，且没有失配的左括号。

那么第一个条件在字符串上等价于：对于字符串 (S) ， (f(S)>0) ，且不存在一个后缀的 (f) 小于 (0) ，即不能存在一个前缀 (S') ，使得 (f(S)<f(S')) 。

这个在树上就等价于：对于点 (u) ，(f(u)>0) ，且不存在点 (v) 在 (u) 到分治边的路径上，使得 (f(u)<f(v)) 。

第二个条件可以类似转化，这里就不细讲了。

因此我们只需要在 (u) 上面存下 (f(u)) 和它到分治边的路径上 (f) 的最值，即可快速判断它应该匹配到哪种串上面去。

同时我们还需要一个桶来存储不同的 (f) 的贡献，这里不展开讲。

最后提醒一下 " 子树大小 " 带来的贡献。假如原先树上的子树大小为 (siz(u)) ，那么分治边祖先的贡献需要特殊计算，而其它的点的贡献就是 (siz) 。

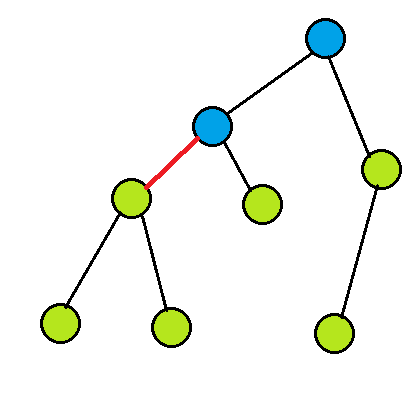
上图中红色的是分治边，蓝色的点就是分治边的祖先，它们的贡献需要特殊计算。

这样做就是 (O(nlog_2n)) 的。

但是常数大得亿亿亿亿匹，人家 300ms ，我就 3s 。

代码

#include <cstdio>
#include <vector>
using namespace std;

typedef long long LL;

const int INF = 0x3f3f3f3f;
const int mod = 998244353;
const int MAXN = 3e5 + 5;

template<typename _T>
inline void read( _T &x )
{
	x = 0;char s = getchar();int f = 1;
	while( s > '9' || s < '0' ){if( s == '-' ) f = -1; s = getchar();}
	while( s >= '0' && s <= '9' ){x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar();}
	x *= f;
}

template<typename _T>
inline void write( _T x )
{
	if( x < 0 ){ putchar( '-' ); x = ( ~ x ) + 1; }
	if( 9 < x ){ write( x / 10 ); }
	putchar( x % 10 + '0' );
}

template<typename _T>
inline _T MAX( const _T a, const _T b )
{
	return a > b ? a : b;
}

template<typename _T>
inline _T MIN( const _T a, const _T b )
{
	return a < b ? a : b;
}

struct edge
{
	int to, nxt;
}Graph[MAXN << 1];

vector<int> T[MAXN];

int f[MAXN], mn[MAXN], mx[MAXN];
int stk[MAXN], top;

int arr1[MAXN << 1], arr2[MAXN << 1];
int *in = arr1 + MAXN, *out = arr2 + MAXN;

int mxw[MAXN];
int dep[MAXN], siz[MAXN], tsiz[MAXN];
int head[MAXN], w[MAXN], con[MAXN];
int N, tot, cnt = 1, ans, color;
char S[MAXN];
bool vis[MAXN];

void sub( int &x, const int v ) { x -= v; x += ( x < 0 ? mod : 0 ); }
void add( int &x, const int v ) { x += v; x -= ( x >= mod ? mod : 0 ); }
int mul( LL x, int y ) { x *= y; if( x >= mod ) x %= mod; return x; }

inline void addEdge( const int from, const int to )
{
	Graph[++ cnt].to = to, Graph[cnt].nxt = head[from];
	head[from] = cnt;
}

inline void addE( const int from, const int to )
{
	addEdge( from, to ), addEdge( to, from );
}

void init( const int u, const int fa )
{
	int lst = 0;
	for( int i = 0, v ; i < T[u].size() ; i ++ )
		if( ( v = T[u][i] ) ^ fa )
		{
			init( v, u );
			if( ! lst ) addE( u, v );
			else addE( lst, ++ tot ), addE( lst = tot, v );
		}
}

void DFS( const int u, const int fa )
{
	tsiz[u] = u <= N, dep[u] = dep[fa] + 1;
	for( int i = head[u], v ; i ; i = Graph[i].nxt )
		if( ( v = Graph[i].to ) ^ fa )
			DFS( v, u ), tsiz[u] += tsiz[v];
}

int getCen( const int u, const int fa, const int all )
{
	siz[u] = 1; int ret = 0, tmp;  
	for( int i = head[u], v, id ; i ; i = Graph[i].nxt )
		if( ( v = Graph[i].to ) ^ fa && ! vis[id = i >> 1] )
		{
			tmp = getCen( v, u, all );
			siz[u] += siz[v];
			mxw[id] = MAX( siz[v], all - siz[v] );
			if( mxw[tmp] < mxw[ret] ) ret = tmp;
			if( mxw[id] < mxw[ret] ) ret = id;
		}
	return ret;
}

void DFS( const int u, const int fa, const int id )
{
	f[u] = f[fa] + w[u], siz[u] = 1;
	mx[u] = MAX( mx[fa], f[u] ), mn[u] = MIN( mn[fa], f[u] );

	if( dep[fa] > dep[u] ) con[u] = N - tsiz[fa];
	else con[u] = tsiz[u];

	if( u <= N )
		switch( id )
		{
			case 0 : 
			{
				stk[++ top] = u;
				if( f[u] <= mn[u] ) add( in[f[u]], con[u] );
				if( f[u] >= mx[u] ) add( out[f[u]], con[u] );
				break;
			}
			case 1 :
			{
				if( f[u] <= mn[u] ) add( ans, mul( out[-f[u]], con[u] ) );
				if( f[u] >= mx[u] ) add( ans, mul( in[-f[u]], con[u] ) ); 
				break;
			}
		}
	
	for( int i = head[u], v ; i ; i = Graph[i].nxt )
		if( ( v = Graph[i].to ) ^ fa && ! vis[i >> 1] )
			DFS( v, u, id ), siz[u] += siz[v];
}

void divide( const int u, const int all )
{
	if( all == 1 ) return ; color ++;
	top = 0;
	int eid = getCen( u, 0, all ); 
	int hu = Graph[eid << 1].to, hv = Graph[eid << 1 | 1].to;
	vis[eid] = true;

	f[hv] = mx[hv] = mn[hv] = 0;
	DFS( hu, hv, 0 ); 
	int t1 = f[hu], t2 = mn[hu], t3 = mx[hu];
	f[hu] = mn[hu] = mx[hu] = 0;
	DFS( hv, hu, 1 );
	f[hu] = t1, mn[hu] = t2, mx[hu] = t3;

	for( int p ; top ; top -- )
	{
		p = stk[top];
		if( f[p] <= mn[p] ) sub( in[f[p]], con[p] );
		if( f[p] >= mx[p] ) sub( out[f[p]], con[p] );
	}

	divide( hu, siz[hu] );
	divide( hv, siz[hv] );
}

int main()
{
	read( N ); scanf( "%s", S + 1 ), tot = N;
	for( int i = 1 ; i <= N ; i ++ ) w[i] = S[i] == '(' ? 1 : -1;
	for( int i = 2, a ; i <= N ; i ++ ) read( a ), T[a].push_back( i ), T[i].push_back( a );
	init( 1, 0 ), DFS( 1, 0 );
	mxw[0] = INF; divide( 1, tot );
	write( ans ), putchar( '
' );
	return 0;
}