[CF932G]Palindrome Partition

题目

        点这里看题目。

分析

        第一步，考虑转换一下题意。
        设(a[i])为任意字符串的第(i)个字符（从(1)标号）。对于两个在原题中要求相等的串——(s_i)和(s_{k-i+1})。令(l=|s_i|)，(n=|S|)，(s_i[1]=S[p])（位置对应）。则：

[s_i=S[p]S[p+1]...S[p+l-1] ]

[s_{k-i+1}=S[n-p-l+2]S[n-p-l+3]...S[n-p+1] ]

        即有：

[forall 0le k<l, S[p+k]=S[n-p-l+1+k] ]

        考虑把(S)倒过来，这就是要求回文性地相等了。考虑构造新串(S'=S[1]S[n]S[2]S[n-1]...S[frac n 2]S[frac n 2+1])，原来的对应关系就变成了一个回文的对应关系。于是原来的一个划分对应了新串上的一个偶回文划分（只能划分出偶回文串）。
        令(S=S')，一个(dp)不难想到：
        (f(i))：前(i)个字符的偶回文划分方案；
        转移：

[f(i)=sum_{0le j<i}f(j)[S[j+1...i] ext{为偶回文串}] ]

        后面的条件可以用回文自动机的(fail)来跳转。
        然后你会发现这其实是(O(n^2))的，(T)了。
        考虑利用性质进行优化。
        对于节点(x)，定义(dif(x)=len(x)-len(fa(x)))。然后我们还可以得到对于(x)，在(fa)的树的(x)的祖先上第一个(dif(w) ot=dif(x))的点，令(slink(x)=w)。
        考虑在(fa)树上，(xsim slink(x))这一段的(dif)其实都是一样的。我们不妨考虑用这个性质进行优化。设(g(x))表示(x)到(slink(x))这一段上面（不包含(slink(x))，它被看做是下一条链的开头）转移位置的(f)的和。那么当(iequiv 0(mod 2))就有(f(i)=sum_p g(p))，也就是从当前的(last)开始，每次跳转到下一个链的开头，然后把这一组的和加起来。
        这只是一些想法，下面结合图片来看一看。
        关于(slink(x))，在下面的图片中，红色的箭头就指向了(x)对应的(slink(x))：

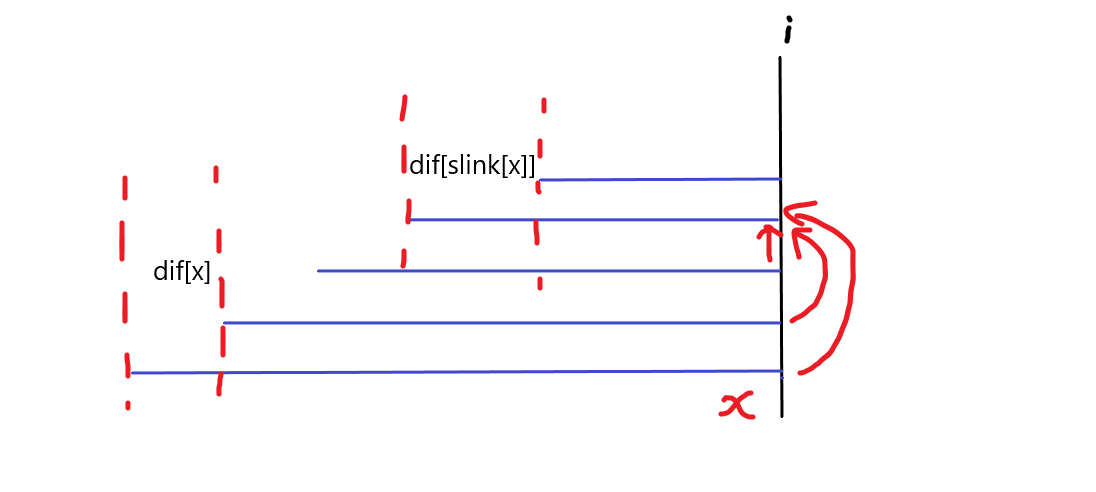
        对于(x)，绿色的线记录了那些(g(x))中应该计算的(f)的位置：

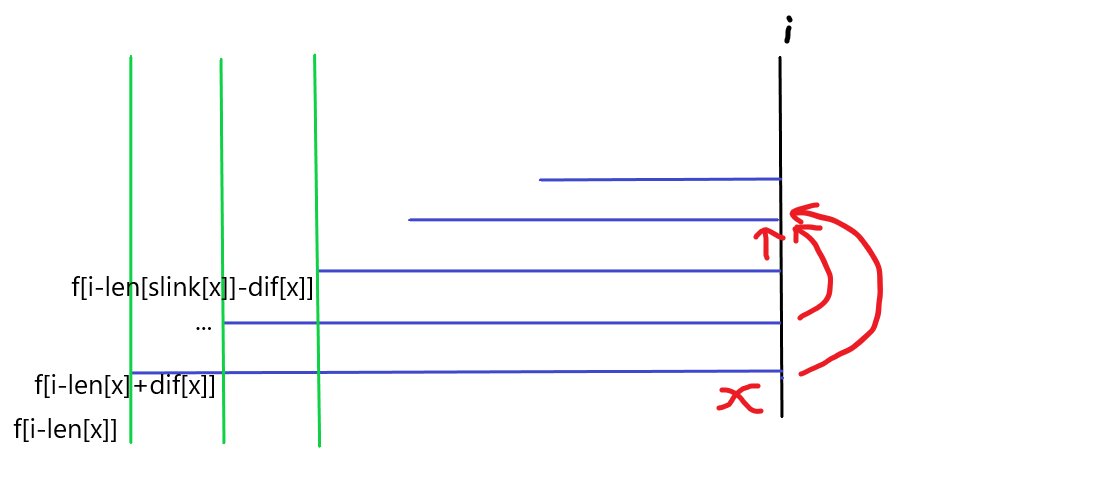
        下面考虑如何转移(g(x))。显然直接对(f)求和是不现实的。不妨来看一下这个情况，当(i=i-dif(x))的时候，我们就已经计算好了(g(fa(x)))了（前提是(fa(x))还和(x)在同一组里面）。根据回文串的性质，我们还可以得到(g(fa(x)))里面对应的(f)的位置：

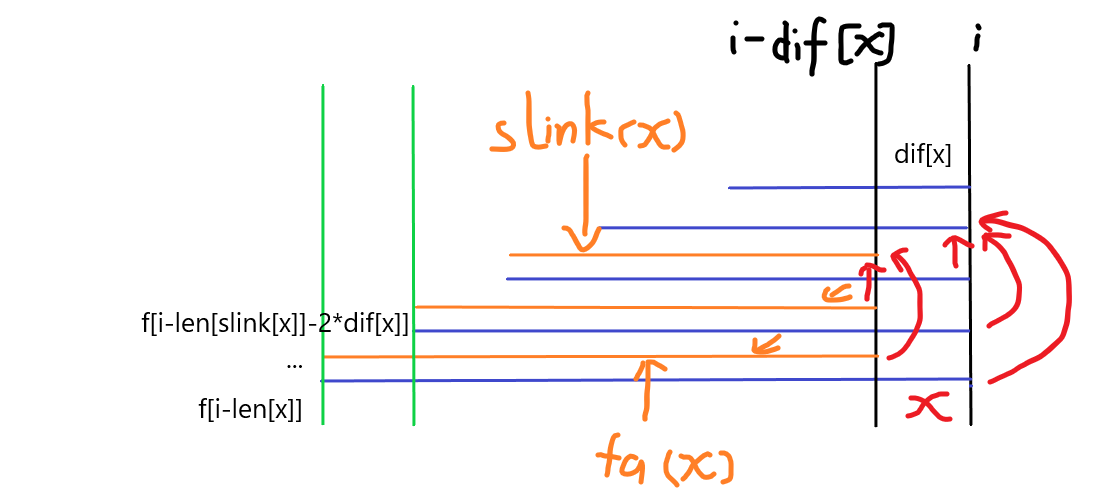
        其中红色箭头指向(slink)。绿色的线表示的是(g(fa(x)))中应计算的(f)的位置。橙色的表示的是，根据回文串的性质，同一组中每个节点的父亲按照自己的回文中心翻转过来的结果。它们的开始的位置都是(i-dif(x))，证明略。因此，(g(fa(x)))实际上在(i-dif(x))的时候就已经被计算了。
        然后你就会发现，(g(fa(x)))相比较于(g(x))，只漏了一个(f(i-len(slink(x))-dif(x)))（因为在(i-dif(x))中，这个转移点的位置正好是(fa(x))的(slink)所翻转过来的），也就是这一组的最后一个串对应的转移点。因此我们只需要在(g(x))中间给它加进去就可以了。需要注意的是，如果(slink(x)=fa(x))，也就是自己就是这一组的最后一个，这样的转移就不能进行。
        出于一些奇特的原因，(slink(x))链的长度似乎是不会超过(O(log_2n))的。我不会证，大家可以去看(yyb)巨佬的博客。洛谷题解区里面也有他的题解。
        于是这道题就被(O(nlog_2n))地解决了。

代码

#include <cstdio>
#include <cstring>

const int mod = 1e9 + 7;
const int MAXN = 1e6 + 5;

template<typename _T>
void read( _T &x )
{
	x = 0; char s = getchar();int f = 1;
	while( s < '0' || '9' < s ) { f = 1; if( s == '-' ) f = -1; s = getchar(); }
	while( '0' <= s && s <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + s - '0', s = getchar(); }
	x *= f;
}

template<typename _T>
void write( _T x )
{
	if( x < 0 ) { putchar( '-' ), x = -x; }
	if( 9 < x ) { write( x / 10 ); }
	putchar( x % 10 + '0' );
}

int g[MAXN], f[MAXN], slink[MAXN], dif[MAXN];
int ch[MAXN][26], fa[MAXN], len[MAXN];
char Snat[MAXN], S[MAXN];
int N, lst, siz;

int main()
{
	scanf( "%s", Snat + 1 ); N = strlen( Snat + 1 );
	for( int i = 1 ; i <= N >> 1 ; i ++ ) S[( i << 1 ) - 1] = Snat[i];
	for( int i = ( N >> 1 ) + 1 ; i <= N ; i ++ ) S[( N - i + 1 ) << 1] = Snat[i];
	int x, p, cur;
	f[0] = 1;
	fa[0] = ++ siz, len[1] = -1;
	for( int i = 1 ; i <= N ; i ++ )
	{
		x = S[i] - 'a';
		while( S[i] ^ S[i - len[lst] - 1] ) lst = fa[lst];
		if( ! ch[lst][x] )
		{
			cur = ++ siz, p = fa[lst]; len[cur] = len[lst] + 2;
			while( S[i] ^ S[i - len[p] - 1] ) p = fa[p];
			fa[cur] = ch[p][x], ch[lst][x] = cur;
			dif[cur] = len[cur] - len[fa[cur]], slink[cur] = ( dif[cur] == dif[fa[cur]] ) ? slink[fa[cur]] : fa[cur];
		}
		lst = ch[lst][x];
		for( p = lst ; p ; p = slink[p] )
		{
			g[p] = f[i - len[slink[p]] - dif[p]];
			if( slink[p] ^ fa[p] ) g[p] = ( g[p] + g[fa[p]] ) % mod;
			if( ! ( i & 1 ) ) f[i] = ( f[i] + g[p] ) % mod;
		}
	}
	write( f[N] ), putchar( '
' );
	return 0;
}