[luogu p1884] [USACO12FEB]Overplanting S

(mathtt{Link})

传送门

(mathtt{Summarization})

在笛卡尔直角坐标系中，给定若干个四边均与坐标轴平行的矩形，求覆盖到的面积。

(mathtt{Solution})

这个题目就是求所有矩形的面积并。

考虑这样一种矩形切割的做法：每到一个矩形 (r)，就用 (r) 来切割之前的所有矩形 (a_i)，将 (a_i) 切割为若干小矩形，加入 (a) 数组，然后删除 (a_i) 这个矩形，加入 (r) 这个矩形。

什么意思呢，举一个例子吧。

我之前有一个矩形 (a_1)，现在来了一个矩形 (r)：

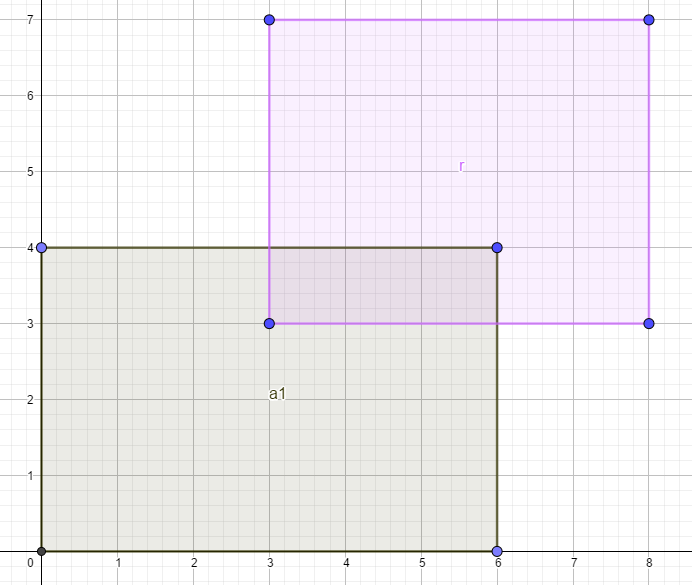
我们用 (r) 切割 (a_1) 后的结果就是这样的：

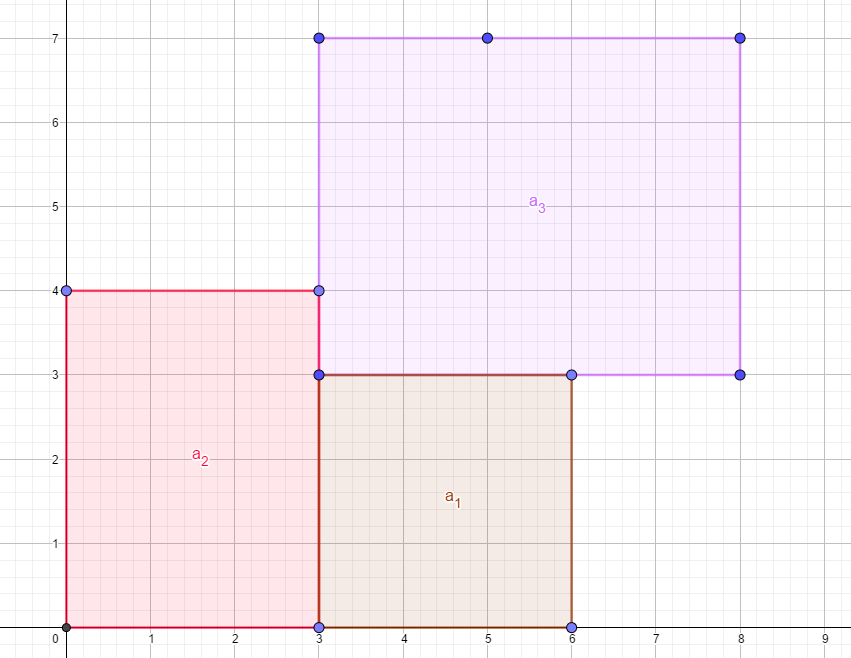
可以看到，(a_1) 没有覆盖到的部分被切割成了两个矩形 (a_1) 和 (a_2)，而重叠那部分人间蒸发了。而 (r) 矩形形状不变，成为了 (a_3)。

此时，一个新矩形 (r) 也来凑热闹了。

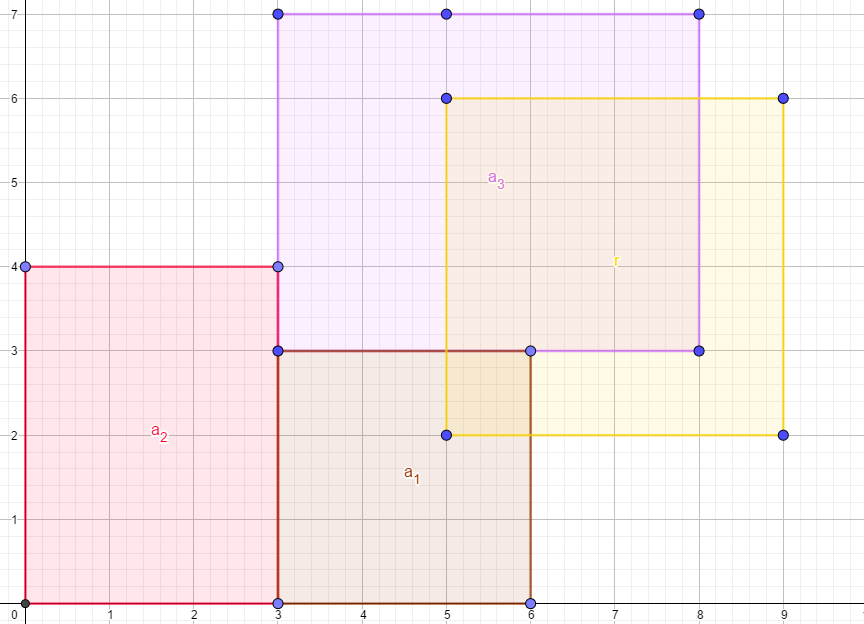
这个 (r) 会轮流查看自己能切到哪些矩形。(a_1, a_3) 可以切到，(a_2) 不行。所以 (r) 会轮流切 (a_1) 和 (a_3)。

先切 (a_1)：

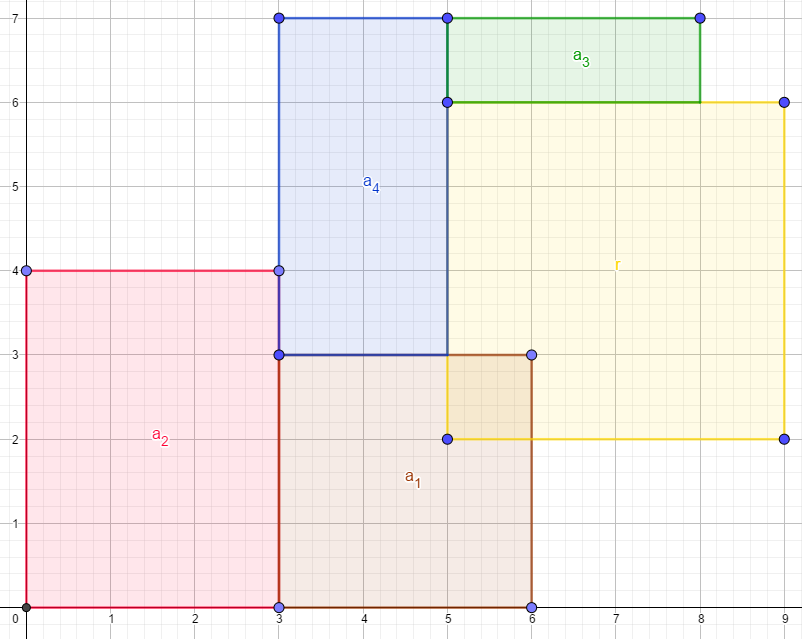
再切 (a_3)，然后入队：

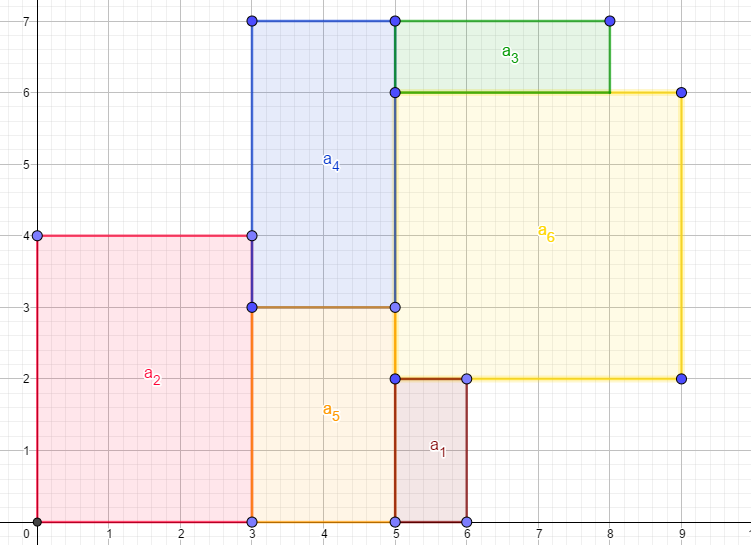
最后，计算每个矩形的面积即可。

思路明朗，代码实现就不难了。

矩形切割的cut函数如下：

void cut(int id, int x1, int y1, int x2, int y2) {
    long long k1, k2, k3, k4;
    k1 = max(a[id].x1, x1);
    k2 = min(a[id].x2, x2);
    k3 = min(a[id].y1, y1);
    k4 = max(a[id].y2, y2);
    if (a[id].x1 < k1) a[++cnt] = (rectangle){a[id].x1, a[id].y1, k1, a[id].y2};
    if (a[id].x2 > k2) a[++cnt] = (rectangle){k2, a[id].y1, a[id].x2, a[id].y2};
    if (a[id].y1 > k3) a[++cnt] = (rectangle){k1, a[id].y1, k2, k3};
    if (a[id].y2 < k4) a[++cnt] = (rectangle){k1, k4, k2, a[id].y2};
}

(mathtt{Code})

/*
 * @Author: crab-in-the-northeast 
 * @Date: 2020-10-31 10:57:53 
 * @Last Modified by:   crab-in-the-northeast 
 * @Last Modified time: 2020-10-31 10:57:53 
 */
#include <iostream>
#include <cstdio>

const int maxn = 1005;
inline long long max(long long a, long long b) {
    return a > b ? a : b;   
}
inline long long min(long long a, long long b) {
    return a < b ? a : b;
}

struct rectangle {
    long long x1, y1;
    long long x2, y2;
}a[maxn];

int cnt = 0;

void cut(int id, int x1, int y1, int x2, int y2) {
    long long k1, k2, k3, k4;
    k1 = max(a[id].x1, x1);
    k2 = min(a[id].x2, x2);
    k3 = min(a[id].y1, y1);
    k4 = max(a[id].y2, y2);
    if (a[id].x1 < k1) a[++cnt] = (rectangle){a[id].x1, a[id].y1, k1, a[id].y2};
    if (a[id].x2 > k2) a[++cnt] = (rectangle){k2, a[id].y1, a[id].x2, a[id].y2};
    if (a[id].y1 > k3) a[++cnt] = (rectangle){k1, a[id].y1, k2, k3};
    if (a[id].y2 < k4) a[++cnt] = (rectangle){k1, k4, k2, a[id].y2};
}

int main() {
    int n;
    std :: scanf("%d", &n);
    
    long long x1, y1, x2, y2;
    std :: scanf("%lld %lld %lld %lld", &x1, &y1, &x2, &y2);
    a[++cnt] = (rectangle){x1, y1, x2, y2};
    for (int i = 2; i <= n; ++i) {
        std :: scanf("%lld %lld %lld %lld", &x1, &y1, &x2, &y2);
        for (int j = 1; j <= cnt; ++j) {
            if (a[j].x1 < x2 && a[j].x2 > x1 && a[j].y1 > y2 && a[j].y2 < y1) {
                cut(j, x1, y1, x2, y2);
                a[j--] = a[cnt--];
            }
        }
        a[++cnt] = (rectangle){x1, y1, x2, y2};
    }

    long long ans = 0;
    for (int i = 1; i <= cnt; ++i)
        ans += (a[i].x2 - a[i].x1) * (a[i].y1 - a[i].y2);
    std :: printf("%lld
", ans);
    return 0;
}

(mathtt{More})

如果使用容斥原理，一个地方可能重复不止两次，所以有可能会算乱。

为了避免这种情况，我们便采用矩形切割这种做法。

好做不乱。

据说本题还可以用线段树+离散化，但是想想就麻烦。。