一、希尔排序(对插入排序进行优化)
原理:1.选定一个增长量h,按h作为分组依据,对数据进行分组
2.对分好组的每一组进行插入排序
3.减少增长量,最少减为一,重复第二步操作

增长量的确定:
int h=1; while(h<数组长度/2){ h=2h+1; } //循环结束后就是最大的h //h的减小规则 h=h/2;
public static void sort(Comparable[] a){ //增长量h int h=1; //根据数组长度来确定增长量h的值 while (h<a.length/2){ h=2*h+1; } //写入排序 while(h>=1){ //排序 //找到待插入元素 for(int i=h;i<a.length;i++){ //把待插入元素插入到有序数列中 for(int j=i;j>=h;j-=h){ //待插元素为a[j],与a[j-h]比较 if(greater(a[j-h],a[j])){ exch(a,j-h,j); }else{ break; } } } //h减少 h=h/2; } }
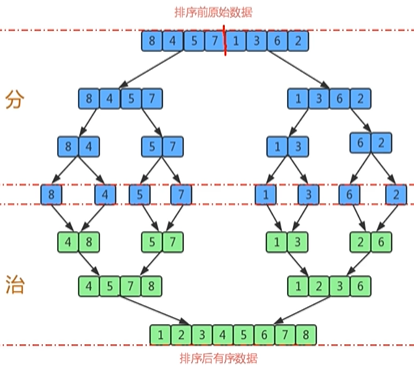
二、归并排序
原理:1. 尽可能的一组数据拆分为相等的两份,并对每一个自组继续进行拆分,直到拆分后每个自组的元素个数为1;
2. 将两个自组合并成一个有序的大组
3.不断重复步骤2,直到成为一个大组
public class Merge { public static void main(String[] args) { //原数组 int[] a={9,8,6,5,2,1}; //归并所需要的复制数组 int[] tem=new int[a.length]; int lo=0; int hi=a.length-1; sort(a,lo,hi,tem); System.out.println(Arrays.toString(a)); } /** *对数组a从lo到hi进行排序 * @param a */ public static void sort(int[] a,int lo,int hi,int[] tem){ if(lo<hi){ //将数组进行分组 int mid=(lo+hi)/2; //分组之后对每一组进行排序 sort(a,lo,mid,tem); sort(a,mid+1,hi,tem); //再把两个数组进行归并 merge(a,lo,hi,mid,tem); } } /** * 对数组,从lo到mid,mid+1到hi两个数组合并排序 */ public static void merge(int[] a,int lo,int hi,int mid,int[] tem){ //此指针指向辅助数组 int i=lo; //此指针指向前数组 int p1=lo; //此指针指向后面的数组 int p2=mid+1; //遍历,移动p1和p2,如果p1指针超过mid或者p2超过mid结束 while(p1<=mid && p2<=hi){ if(a[p1]<a[p2]){ tem[i++]=a[p1++];//把a[p1]给辅助数组,并且指针后移 }else{ tem[i++]=a[p2++]; } } //如果p1指针指向的数组没遍历完,那么直接赋给tem while (p1<=mid){ tem[i++]=a[p1++]; } //如果p2指针指向的数组没遍历完,那么直接赋给tem while (p2<=hi){ tem[i++]=a[p2++]; } //把assist数组拷贝到a数组中 for (int index=lo;index<=hi;index++){ a[index]=tem[index]; } } }
三、快速排序
原理:快速排序是对冒泡排序的改进;
1. 首先选定一个分界值,将数组分为两部分
2. 将大于等于分界值的数据放到右边,小于的放到左边
3. 对左边和右边分别进行2步骤
4. 重复上述步骤,通过递归对左右两部分进行排序,最后完成

把一个数组切分为两个数组的原理:
1.找一个基准值(一般为第一个元素,6),用两个指针分别指向数组的头部和尾部+1的位置
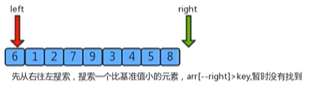
2.先从尾部向头部开始搜索一个比基准值小的元素,并停止,记录元素。
3.再从头部向尾部开始搜索一个比基准值小的元素,并停止,记录元素。
4.交换左右指针所指的值。
5.重复上述操作
public class Partition{ public static void main(String[] args) { //原数组 int[] a={1,6,2,12,9,10}; int lo=0; int hi=a.length-1; sort(a,lo,hi); System.out.println(Arrays.toString(a)); } /** *对数组a从lo到hi进行排序 * @param a */ public static void sort(int[] a,int lo,int hi){ if (lo<hi){ //对数组a从lo到hi进行分组(左和右子组),返回分界索引 int partition = partition(a, lo, hi); //对左子组进行排序 sort(a,lo,partition-1); //对右子组进行排序 sort(a,partition+1,hi); } } /** * 对数组,从lo到hi两个数组进行分组并返回分界索引 */ public static int partition(int[] a,int lo,int hi) { //分界值 int key=a[lo]; //头指针 int left=lo; //尾指针的下一个位置 int right=hi+1; while (true) { //先从右往左扫描,移动right,如果right所指的值小于key则停止 while (a[--right]>key){ if(right==lo){ break; } } //从左往右扫描,移动left,如果left所指的值大于key则停止 while (a[++left]<key){ if (left==hi){ break; } } //判断left>=right,则扫描完毕,结束循环,如果不是则交换元素 if (left>=right){ break; }else { exch(a,left,right); } } exch(a,lo,right); return right; } private static void exch(int[] a, int hi, int lo) { int temp = 0; temp =a[lo]; a[lo]=a[hi]; a[hi]=temp; } }
四、排序的稳定性
1.定义:假设数组a中右若干元素,其中A和B相等,在A在B的前面,在排完序之后任能保证A在B的前面,则稳定
2.常见排序算法的稳定性
稳定的:排序、插入、归并
不稳定的:选择、希尔、快速