Bogo排序

在计算机科学中，Bogo排序（bogo-sort）是个既不实用又原始的排序算法，其原理等同将一堆卡片抛起，落在桌上后检查卡片是否已整齐排列好，若非就再抛一次。其名字源自Quantum bogodynamics，又称bozo sort、blort sort或猴子排序.

实现

以下是C代码：

#include<stdio.h>    
#include<string.h>   
#include<math.h>   
#include<ctype.h>   
#include<stdbool.h>
#include<stdlib.h>
#include<time.h>

void swap(int *a, int *b)   //交换两元素的值
{
    int t;
    t=*a;
    *a=*b;
    *b=t;
}

void printArray(int a[], int count)   //打印数组元素
{
    int i;
    for(i=0; i<count; i++)
        printf("%d ",a[i]);
    printf("\n");
}

unsigned int Random1(int a, int b)  //随机生成[a,b)之间的数
{
    return (rand()%(b-a)+a);
}

unsigned int Random2(int n)  //随机生成[0,n)之间的数
{
    return (rand()%n);
}

bool inorder(int a[], int n)  //判断序列是否已经有序
{
    int i;
    for(i=0; i<n; i++)
    {
        if(a[i] > a[i+1])  return false;
    }
    return true;
}

void shuffle(int a[], int n)
{
    int i,swapPosition;
    for(i=0; i<n; i++)
    {
        swapPosition = Random2(i+1);
        swap(&a[i],&a[swapPosition]);
    }
}
 
void bogo_sort(int a[], int n)
{
    while(!inorder(a,n))
        shuffle(a,n);
}

int main(void)   
{
    int a[]={3, 5, 4, 6, 9, 7, 8, 0, 1};
    int n=sizeof(a)/sizeof(*a);
    srand((unsigned)time(NULL));  
    printArray(a,n);
    bogo_sort(a,n);
    printArray(a,n);    
    return 0;
}

其平均时间复杂度是 O(n × n!)，在最坏情况所需时间是无限。它并非一个稳定的算法。

运行时间

      这个排序算法基于可能性。平均而言，让所有元素都被排好序的期望比较次数渐近于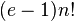，期望的位置交换次数渐近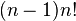。期望的位置交换次数增长地比期望比较次数快，是因为只需要比较几对元素就能发现元素是无序的，但是随机地打乱顺序所需要的交换次数却与数据长度成比例。在最差的情况下，交换和比较次数都是无限的，这就像随机投掷硬币可能连续任意次正面向上。

最好的情况是所给的数据是已经排好序的，这种情况下不需要任何位置交换，而比较次数等于。

对任何固定长度的数据，算法的预期运行时间像无限猴子定理一样是无限的：总有一些可能性让被正确排好序的序列出现。