从如何判断浮点数是否等于0说起——浮点数的机器级表示（转）

http://www.cnblogs.com/kubixuesheng/p/4107309.html

这位前辈讲的不错，摘抄下来以表尊敬！

void isZero(double d)
    {
        if (d >= -DBL_EPSILON && d <= DBL_EPSILON)
        {
            //d是0处理
        }
    }

    void isZero(int d)
    {
        if (0 == d)
        {
            //d是0处理
        }
    }

    void isZero(int *d)
    {
        if (NULL == d)
        {
            //d是空指针处理
        }
    }

    void isZero(bool d)
    {
        if (!d)
        {
            //d就认为是false 也就是0
        }
    }

没错，很多经典的教科书或者指南，一些技术类的讲义，都会这样教授。但是为什么要这样写？

可能一部分人就糊涂了，不知道咋回答，搞技术或者做学问不是诗词歌赋，结论经不起严谨的推敲就不能服众，不可以说，书上是这样写的，或者老师告诉我的，那样太low了。尤其是浮点数比较的问题，不只是0，类似的和其他的浮点数比较大小的问题也是一样的。

要解决这个疑惑，必须先理解计算机是如何表示和存储浮点数据的，期间参考了IEEE单双精度的规范文档，和MSDN的一些文档，以及《深入理解计算机操作系统》一书。

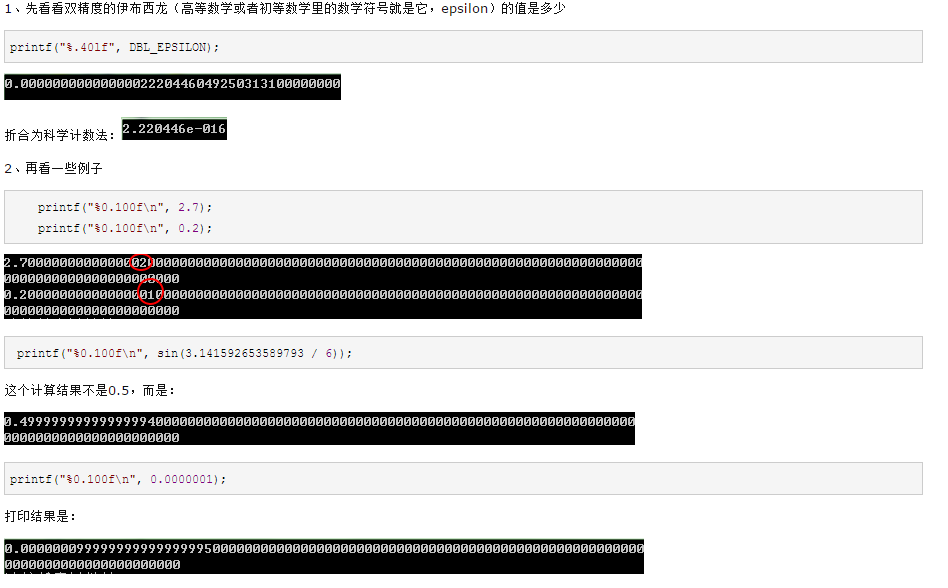
这样的结果在不同机器或者编译器下，有可能不同，但是能说明一个问题，浮点数的比较，不能简单的使用==，而科学的做法是依靠EPISILON，这个比较小的正数（英文单词episilon的中文解释）。

EPSILON被规定为是最小误差，换句话说就是使得EPSILON+1.0不等于1.0的最小的正数，也就是如果正数d小于EPISILON，那么d和1.0相加，计算机就认为还是等于1.0，这个EPISILON是变和不变的临界值。

#define DBL_EPSILON      2.2204460492503131E-16 
2 #define FLT_EPSILON     1.19209290E-07F 
3 #define LDBL_EPSILON     1.084202172485504E-19 

浮点数表达的有效位数（也就是俗称的精度）和表达范围不是一个意思

经常说什么单精度一般小数点精度是7-8位，双精度是15-16位，到低怎么来的呢？前面说了，单精度数尾数23位，加上默认的小数点前的1位1，2^(23+1) = 16777216。关键： 10^7 < 16777216 < 10^8，所以说单精度浮点数的有效位数是7-8位，这个7-8位说的是十进制下的，而我们前面说的尾数位数那是二进制下的，需要转换。

又看，双精度的尾数52位存储，2^(52+1) = 9007199254740992，那么有10^16 < 9007199254740992 < 10^17，所以双精度的有效位数是16-17位。

貌似实际编码中，大部分直接用double了，省的出错。