PLSA模型是基于频率派思想的，每篇文档的K个主题是固定的，每个主题的词语概率也是固定的，我们最终要求出固定的topic-word概率模型。贝叶斯学派显然不认同，他们认为，文档的主题未知，主题的词语分布未知，我们无法求解出精确值，只能计算doc-topic概率模型、topic-word概率模型的概率分布。
LDA模型文档生成过程
我们令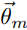
为doc-topic概率模型，
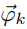为topic-word概率模型，每个
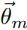包含K个维度（K为topic类数量），每个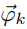包含V个维度（V为word类数量）。在PLSA中，抛doc-topic骰子是一个K项式实验，抛topic-word骰子是一个V项式实验，所以我们使用K维Dirichlet分布模拟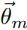的先验分布，V维Dirichlet分布模拟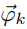的先验分布是自然而然的事情。使用贝叶斯思想改造PLSA模型后，得到的新模型叫做LDA模型。LDA模型文档生成图例如下
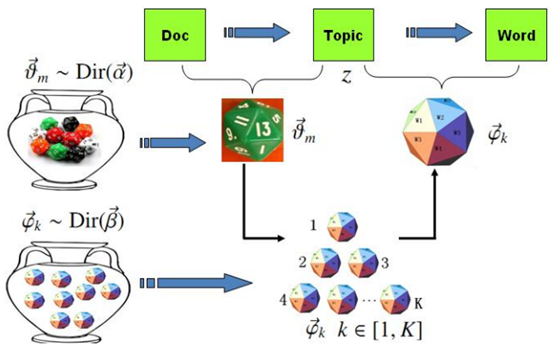
由于topic-word模型与文档无关，所以我们在所有文档生成之前从Dirichlet分布生成K个topic-word骰子。而doc-topic模型和每篇文档相关，所以生成每篇文档之前需要从Dirichlet分布生成1个doc-topic骰子。LDA模型生成文档过程如下
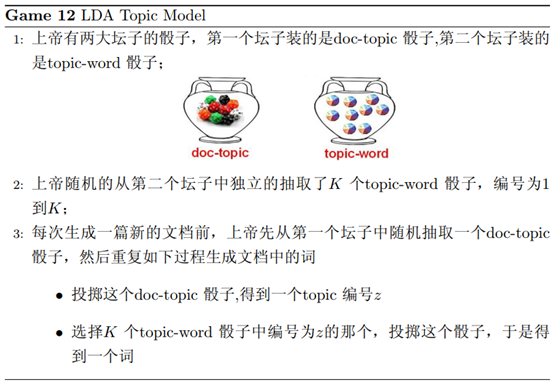
LDA模型的物理分解
物理过程分解
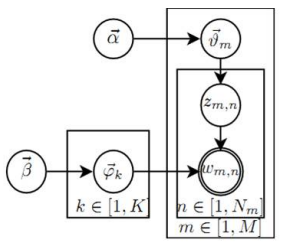
对于第m篇文档第n个词语的生成，我们可以分解为如下两个过程
1、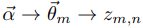 
通过Dirichlet(α)分布生成一个doc-topic骰子m，投掷doc-topic骰子m，进行K项式实验，生成topic z(1 <= z <= K)。
2、 
事先已经通过Dirichlet(β)分布生成了K个topic-word骰子（编号1到K），选择第z个骰子投掷，进行V项式实验，生成词语w。
LDA模型的数学描述
对于第一个物理过程显然是Dirichlet-Multinomial共轭结构
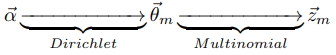
对比下面公式（公式懒得敲，复制《LDA数学八卦》，其实就是多项式分布在Dirichlet分布上积分）
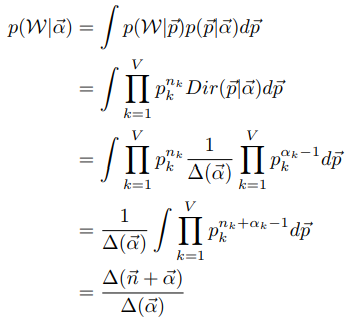
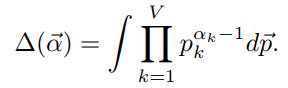
我们有
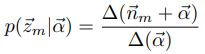
其中
表示第m篇文档第k个topic产生词语的个数（也就是第k个topic投掷出现的次数，n对于我们来说是未知的）。参数的后验分布为
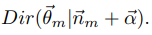
由于语料中M篇文档相互独立，所以我们得到M个相互独立的Dirichlet-Multinomial共轭结构，从而整个语料库topic生成的概率为
（1）
由于topic-word概率分布与doc数量无关，对于K个topic-word骰子，我们有K个Dirichlet分布，理所当然我们应该有K个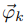
的Dirichlet-Multinomial共轭结构。
前面的LDA过程我们不好找出K个topic-word骰子V项式实验，我们进行一下改造。
1、 每篇文章每个词进行一次doc-topic骰子多项式投掷实验与一次topic-word骰子多项式投掷实验。
修改为
2、 每篇文章先进行n次doc-topic骰子多项式投掷实验，再进行n次topic-word骰子多项式投掷实验。（n为一篇文章中词语的个数）
进一步修改
3、 整个语料库先进行n次doc-topic骰子多项式投掷实验，并且把实验结果分成K类，每类对应同一个topic结果，然后再在K类中分别进行topic-word骰子多项式投掷实验，总共n次。（n为整个语料库的词语个数）
这里在K类中分别进行topic-word骰子多项式投掷实验，显然就是K个topic-word骰子V项式实验。上述过程可以用如下两个表达式表示
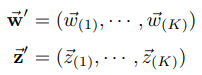
z表示进行的M个doc-topic多项式投掷实验生成的结果（每篇文章用一个doc-topic骰子，结果进行了分类排序），w表示进行了K个topic-word多项式投掷实验（每个主题用一个topic-word骰子）。
因此第二个物理过程也是一个Dirichlet-Multinomial共轭结构
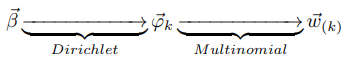
我们有
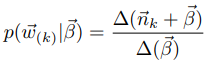
其中
表示第k个topic产生第word t的个数（n未知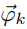），的后验分布为
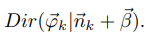
由于K个topic生成word是独立的，所以我们得到了K个独立的Dirichlet-Multinomial共轭结构，于是整个语料的词语生成概率为
（2）
由于生成topic和word是独立的，综合（1）（2）有
参考：《LDA数学八卦》