线性回归的应用——容量预测

一个发展中的电信市场，网络容量往往是线性增加的，我们可以通过拟合历史网络容量指标，来判断未来网络规模，从而提前进行网络扩容，防患于未然。

线性回归实际上是找到一条直线，使得所有观测点y值到直线的离差平方和最小。

一、多元线性回归

多元线性回归使用矩阵方程可以很好的描述：

1、 拟合的p元线性方式格式

2、 回归拟合直线满足观测值与理论值离差平方和最小

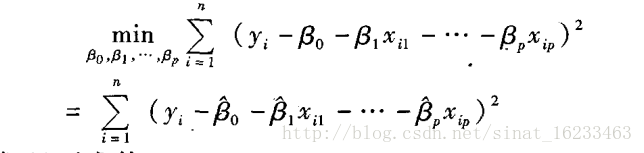
3、 分别对p+1个因变量系数Beta求导，得到如下方程组

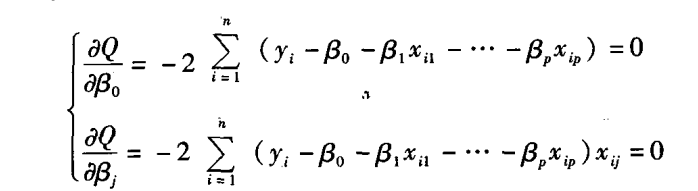
4、 进一步化简

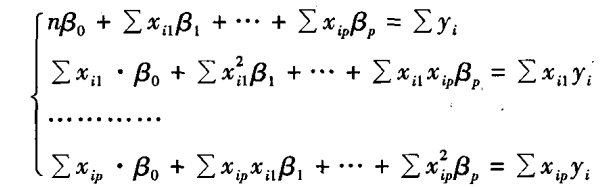
5、 采用矩阵形式表示方程

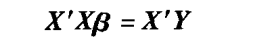
6、 则方程系数如下

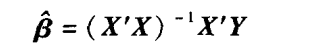
二、一元线性回归

在实际应用场景中，一元线性回归应用较广，求解方法十分简单，下面详细介绍一下一元线性回归的最小二乘法，百度百科介绍如下：

1. 列计算表，求∑x，∑xx，∑y，∑yy，∑xy；

2. 计算Lxx，Lyy，Lxy；

Lxx=∑(x-xˇ)(x-xˇ)

Lyy=∑(y-yˇ)(y-yˇ)

Lxy=∑(x-xˇ)(y-yˇ)

3. 求相关系数，并检验；

r = Lxy /( Lxx Lyy)1/2

2. 求回归系数b和常数a；

b=Lxy /Lxx

a=y - bx

3. 列回归方程。

其中r^2表示y的变化受x变化的影响程度。如果所有观测点都落在拟合直线上，r^2 = 1； 如果观测点左右对称，r^2 = 0。相关系数是评判拟合直线准确性的一个重要指标，r^2越大，对于拟合直线的预测理论上越可信。

一元线性回归代码

package com.coshaho.learn;

/**
 * 
 * LineRegression.java Create on 2017年5月28日 下午9:38:47    
 *    
 * 类功能说明:  一元线性回归 
 *
 * Copyright: Copyright(c) 2013 
 * Company: COSHAHO
 * @Version 1.0
 * @Author coshaho
 */
public class LineRegression 
{
    private float Lxx = 0;
    private float Lyy = 0;
    private float Lxy = 0;
    private float avgx = 0;
    private float avgy = 0;
    private int n = 0;
    // 因变量系数
    private float a = 0;
    // 方程常量
    private float b = 0;
    // 相关系数
    private double r = 0;
    private double r2 = 0;
    
    public boolean init(int[] xs, int[] ys)
    {
        if(null == xs || null == ys)
        {
            return false;
        }
        
        if(1 == xs.length || 1 == ys.length)
        {
            return false;
        }
        
        if(xs.length != ys.length)
        {
            return false;
        }
        caculate(xs, ys);
        return true;
    }
    
    private void caculate(int[] xs, int[] ys)
    {
        refresh();
        n = xs.length;
        
        for(int x : xs)
        {
            avgx = avgx + x;
        }
        avgx = avgx / n;
        
        for(int y : ys)
        {
            avgy = avgy + y;
        }
        avgy = avgy / n;
        
        for(int x : xs)
        {
            Lxx = Lxx + (x - avgx) * (x - avgx);
        }
        
        for(int y : ys)
        {
            Lyy = Lyy + (y - avgy) * (y - avgy);
        }
        
        for(int i = 0; i < n; i++)
        {
            Lxy = Lxy + (xs[i] - avgx) * (ys[i] - avgy);
        }
        
        a = Lxy / Lxx;
        b = avgy - a * avgx;
        r = Lxy / Math.sqrt(Lxx * Lyy);
        r2 = r * r;
    }
    
    private void refresh()
    {
        Lxx = 0;
        Lyy = 0;
        Lxy = 0;
        avgx = 0;
        avgy = 0;
        n = 0;
        a = 0;
        b = 0;
        r = 0;
        r2 = 0;
    }

    public float getA() 
    {
        return a;
    }

    public float getB()
    {
        return b;
    }

    public double getR() 
    {
        return r;
    }
    
    public double getR2() 
    {
        return r2;
    }

    public static void main(String[] args)
    {
        LineRegression line = new LineRegression();
        int[] xs = {1, 2, 3, 4, 5};
        int[] ys = {100, 80, 60, 80, 100};
        line.init(xs, ys);
        System.out.println("y = " + line.getA() + "x + " + line.getB());
        System.out.println("r^2 = " + line.getR2());
        
        int[] xs1 = {1, 2, 3, 4, 5};
        int[] ys1 = {100, 110, 130, 140, 170};
        line.init(xs1, ys1);
        System.out.println("y = " + line.getA() + "x + " + line.getB());
        System.out.println("r^2 = " + line.getR2());
    }
}