机器学习数学【1】

概率 & 统计

Lary Wasserman《All of Statistics》

概率：给定数据生成过程，那么输出的性质是怎样

统计：给定输出结果，那么生成数据的过程是怎样

统计 vs 机器学习

统计	机器学习
Models Parameters Fitting, Estimate Regression/Classification Clustering,Density estimation	Network, Graph Weights Learning Supervised Learning Unsupervised Learning

随机试验

所有试验结果构成样本空间，随机事件是样本空间的子集

概率三大公理：

$P(E) in R, P(E)geq 0, forall E in F$

$P(Omega)=1$

$P(U^infty _iE_i)=sum_{i=1}^infty P(E_i)$ $E_i$间互斥

随机变量

离散数据：PMF probability mass function 概率质量函数  $P(X=x)$

连续数据：PDF probability density function  概率密度函数  $f(x)=frac{dF(x)}{dx}$

CDF cumulative distribution function 累积分布函数(分布函数) $F(x)=P(Xleq x)$，是PDF的积分

多维随机变量

一次随机试验关注多个维度

联合分布：$P(Xleq x, Yleq y)$

边缘分布：$P(Xleq x)=sum P(Xleq x, Yleq +infty)$

条件分布：$P(Xleq x|Yleq y)=frac{P(Xleq x,Yleq y)}{P(Yleq y)}$

随机变量数字特征

• 众数：Mode，最可能出现的值
• 中位数：Mdedian，$P(Xgeq median)=P(Xleq mddian)=0.5$
• 期望：Expectation，反复抽样，期望得到的平均值

N阶矩：原点矩(c=0)&中心矩(c=期望)：$mu_n = int_{-infty}^{-infty}(x-c)^nf(x)dx$

归一化N阶中心矩 $frac{mu_n}{sigma^n}=frac{E[(X-mu)^n]}{sigma^n}$

N阶矩	原点矩	中心矩阵	归一化中心矩	表征(PDF)
1	期望			中心
2		方差		胖瘦
3			偏度	偏向skewness
4			峰度	尖锐度Kurtosis

• 方差

• 偏度

$gamma_1 = E[(frac{X-mu}{sigma})^3]=frac{mu_3}{sigma^3}=frac{E[(X-mu)^3]}{(E[(X-mu)^2])^{3/2}}=frac{kappa_3}{kappa_2^{3/2}}$

• 峰度

$Kurt[X] = E[(frac{X-mu}{sigma})^4]=frac{mu_4}{sigma^4}=frac{E[(X-mu)^4]}{(E[(X-mu)^2])^{2}}$

• 特征函数：频域变化，pdf的傅里叶变换

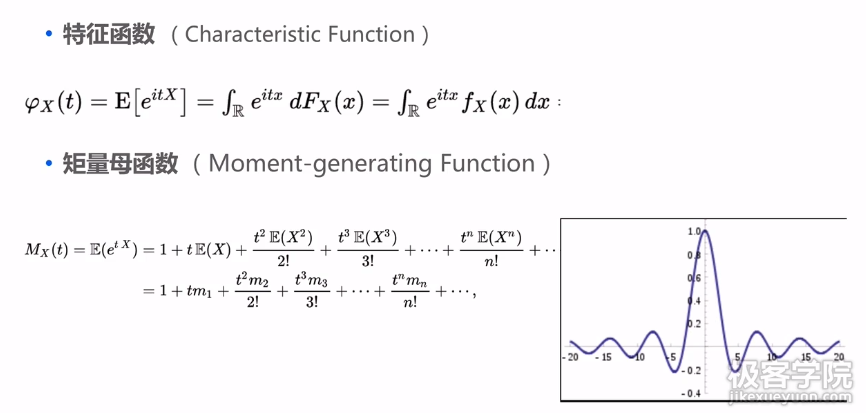
• 协方差：衡量两个变量的线性相关性

$Cov(X,Y)=E[(X-E[X])(Y-E[Y])]=E[XY]-E[X]E[Y]$

正相关：X越大，Y越大

负相关：X越大，Y越小

不相关：X和Y的变化没有关系

• 相关系数：标准化后的协方差

$ ho (X,Y)=frac{Cov(X,Y)}{sigma(X)sigma(Y)}$

• 余弦相似度：两个向量的相似度，余弦相似度玉相关系数的计算是一样的

$vec{X}=[(X_1-E[X])...(X_n-E[X])]$

$vec{Y}=[(Y_1-E[Y])...(Y_n-E[Y])]$

$r=frac{sum_{i=1}^n((X_i-E[X])(Y_i-E[Y]))}{sqrt{sum_{i=1}^n(X_i-E[X])^2}sqrt{sum_{i=1}^n(Y_i-E[y])^2}}$

四个定理

1. 贝叶斯定理(条件概率)

$P(A|B)=frac{P(AB)}{P(B)}=frac{P(B|A)P(A)}{P(B)}$

2. 全概率公式

$P(A)=P(AB)=sum_nP(AB_n)=sum_nP(A|B_n)P(B_n)$

一个事件A的发生，等同于该事件与一个完备数据集B同时发生的情况

而$P(B)=sum_nP(B_n)$，$B={B_1,B_2...B_n}$是一个完备事件组(各事件互斥，所有事件概率和为1)，

$P(A)$就可以看成是A与B中所有可能情况同时发生的概率和

把复杂的事情分情况求解~

3. 大数定理

这个“大”，是数据量要很大的意思吧~当数据很大时，实验值就会接近于理论值

• 强大数定理

$Pr(lim_{n ightarrow infty} frac{X_1+X_2...+X_n}{n}=mu)=1$

随着样本量增加，样本均值以概率1收敛于期望（样本均值很接近期望）

• 博雷尔强大数定理

$Pr(lim_{n ightarrow infty} frac{V_n}{n}=p)=1$

随着样本量的增大，频率以概率1收敛于概率(实验中，一个事件发生的频率接近其概率)

4. 中心极限定理

Lindeberg-Levy中心极限定理：假设${X_1, X_2,...}$是i.i.d(独立同分布)的随机变量，且$E[X_i]=mu,Var[X_i]=sigma^2$，那么

$sum_{i=1}^nX_ioverset{d}{ ightarrow}N(nmu,nsigma^2)$，也就是

样本足够多时，样本的均值呈正态分布

随机数生成方法

1.Inverse Transform Sampling(Inverse CDF)

目标：生成CDF为F(x)的变量

步骤：

• 从[0,1]的均匀分布中随机采样得到$U$
• 计算$X=F^{-1}_X(U)$逆函数（逆函数的定义域、值域对应原函数的值域、定义域，就是反过来的，也就是$U=F(x)$）

import numpy as np
from scipy.special import erfinv
 
#生成服从高斯分布
def inverfsampling(mu=0, sigma=1, size=1):
     z = np.sqrt(2)*erfinv(2*np.random.uniform(size=size)-1)
     return mu+z*sigma

2. 拒绝采样（Reject Sampling）

目标：生成服从$ ilde{p}(x)$分布的变量

基本思想：可以容易地生成$q(x)$随机变量，在$q(x)$中采样，如果采样点符合$ ilde{p}(x)$则接受，否则拒绝

步骤：

• 从$q(x)$中采样得到$z_0$
• 从$[0,kq(z_0)]$均匀分布采样得到$u_0$（为什么用$kq(z_0)$：这里$kq(x)$是希望可以完全包含住$ ilde{p}(x)$）
• 检查$u_0< ilde{p}(z_0)$是否成立。若成立则接受$z_0$，否则拒绝

说明：

概率密度函数图，红色为$ ilde{p}(x)，蓝色为q(x)$

采样结果分布：蓝色和红色接近的位置点比较多（接受率高），概率高，与红色分布类似

接受率：$p(accept)=int frac{ ilde{p}(z)}{kq(z)}q(z)dz=frac{1}{k}int ilde{p}(z)dz$

接受率与$k$相关，当$k$比较大时，采样效率比较低=>自适应采样

实例

# p(z)=0.3exp(-(z-0.3)^2)+0.7exp(-(z-2)^2/0.3)
import numpy as np
from scipy.special import erfinv

def rejectSampling():
    size = 10
    z = np.random.normal(loc=1.4,scal=1.2,size=size)
    sigma=1.2
    qz=1/(np.sqrt(2*np.pi)*sigma**2)*np.exp(-0.5*(z-1.4)**2/sigma**2)
    k=3
    u=np.random.uniform(low=0,high=k*qa,size=size)
    pz=0.3*np.exp(-(z-0.3)**2)+0.7*np.exp(-(z-2.)**2/0.3)
    sample=z[pz>=u]
    print z

3. Box-Muller

用于产生高斯分布随机变量（常用方法）

步骤：

• 从[0,1]均匀分布中随机采样得到$U_1$和$U_2$
• 计算$z_0=Rcos(Theta )=sqrt{-2lnU_1}cos(2pi U_2)$
• $z_0$服从标准正态分布

实例

import numpy as np
from scipy.special import erfinv

def boxmullersampling(mu=0, sigma=1,size=1):
    u=np.random.uniform(size=size)
    v=np.random.uniform(size=size)
    z=np.sqrt(-2*np.log(u))*np.cos(2*np.pi*v)
    return mu+z*sigma

参考

• PaddlePaddle训练营公开课
• 【概率论与数理统计】小结6 - 大数定理与中心极限定理