对梯度概念的直观理解

一滴水，沿着玻璃往下滚动，轨迹就是梯度的反方向。

 

我们先来玩一个游戏，假如你在一座山上，蒙着眼睛，但是你必须到达山谷中最低点的湖泊，你该怎么办？

梯度可以帮助你完成这个游戏。

梯度和方向导数紧密相关，让我们从方向导数开始。

1. 方向导数

---------------------------------------------------------

顾名思义，方向导数就是某个方向上的导数。

什么是方向：

函数在这个方向上的图像：

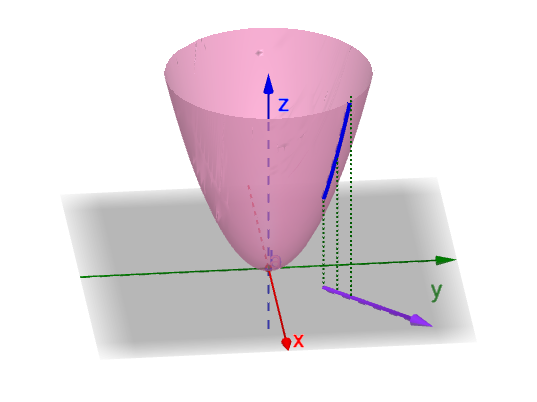
我们知道：

函数的点在这个方向上也是有切线的，其切线的斜率就是方向导数：

我之前在什么是全导数、偏导数、方向导数？这个回答中，已经全面回答过什么是方向导数了。感兴趣可以看看。

2. 梯度

--------------------------------------------------------- 

很显然，点不止一个方向，而是都有方向：

每个方向都是有方向导数的：

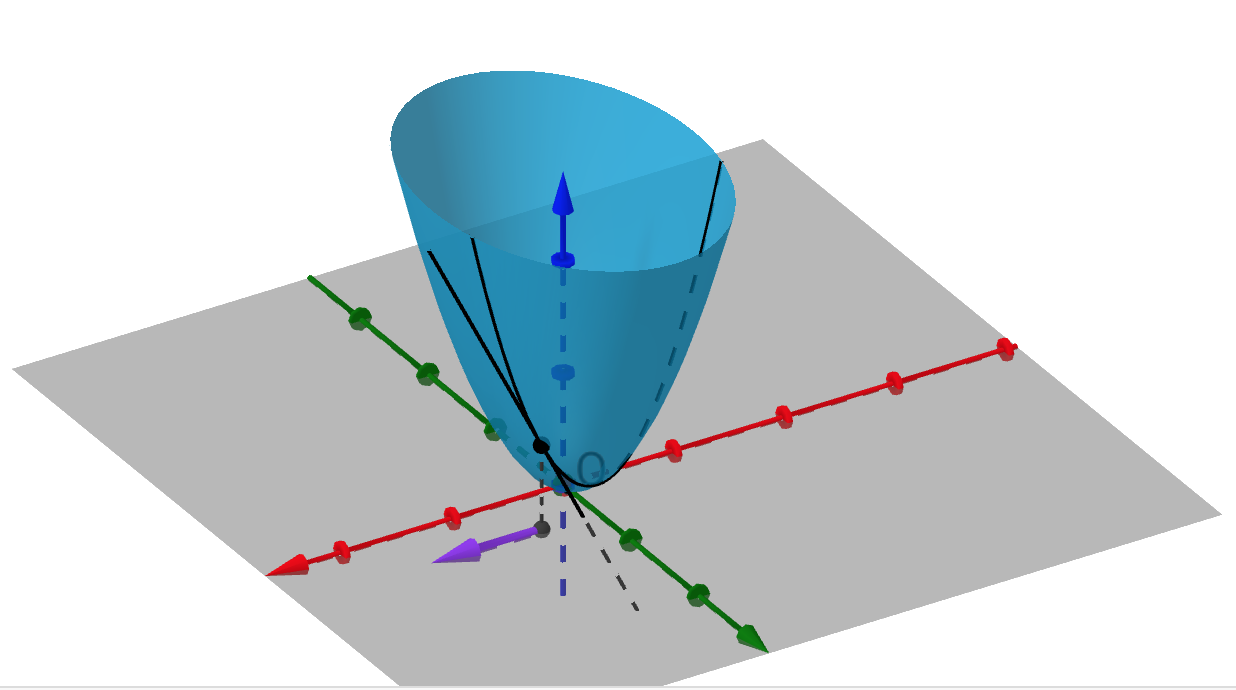
这就引出了梯度的定义：

梯度：是一个矢量，其方向上的方向导数最大，其大小正好是此最大方向导数。

定义出来了，并不复杂，但对于我而言这才是开始，因为我还有两个疑问：

• 为什么所有方向导数中会存在并且只存在一个最大值？而不是有多个最大值、或者说没有最大值？
• 这个最大值在哪个方向取得？值是多少？

 2.1 为什么所有方向导数中会存在并且只存在一个最大值？