在图论和网络中,度(degree)是指网络(图)中一个点的与其他点的连接数量,度分布(Degree Distribution)就是整个网络中,各个点的度数量的概率分布。
对于有向图,有入度(in-degree)和出度(out-degree),入度是指指向该节点的边的数量,出度是指从该节点出发指向其他节点的边的数量。
度分布P(k)是指,网络中,度为k的节点的出现概率;对于有向图来说又分为入度分布和出度分布。如果网络中总共有n个节点,其中有nk个节点,他的度为k,那么P(K)=nk/n。
累计度分布(cumulative degree distribution)就是度数大于或者等于k的节点出现的概率。
度分布对于真实网络(如互联网、社会网络、理论网(theoretical networks)等)研究非常的重要。其中,最简单的网络模型-伯努利随机图(任何两个节点连接的概率是独立的,概率为P),则其度分布应该为,
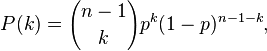
但是,真实网络中的度分布是与之不同,许多是右偏的(right-skewed),即,有大量的度比较小的节点,少量度比较大的节点。一些网络中,尤其是互联网和社会网络中,发现度分布往往近似于指数分布(power law),P(k) ~ k−γ,γ是一个常数。这样的网络被称为无标度网络(scale-free networks),对于他的结构和动态特性,引起了人们的广泛关注。
翻译自:http://en.wikipedia.org/wiki/Degree_distribution