题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6395
因为题目数据范围太大,又存在递推关系,用矩阵快速幂来加快递推。
每一项递推时 加的下取整的数随着n变化,但因为下取整有连续性(n一段区间下取整的数是相同的),可以分块,相同的用矩阵快速幂加速
想了好久。。如果最小的开始的值是【p/i】的数为i,那连续的一段长度是【p/(p/i)】-i+1,但为什么分段数是根号n级别啊?。。。
套矩阵快速幂,时间复杂度O(sqrt(n) * log(n))
⎧⎩⎨⎪⎪⎪⎪⎪⎪F
⎧⎩⎨⎪⎪⎪⎪⎪⎪F
一个递推关系式 可以用矩阵乘法来表示递推关系
可以用矩阵乘法来表示递推关系
有两种写法
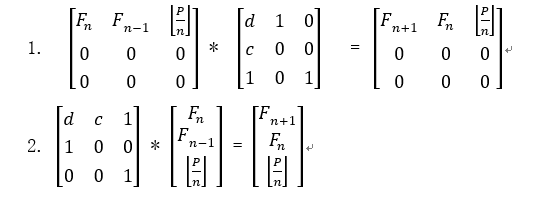
至于怎么求特征值矩阵(用来加速的那个矩阵),就是根据关系式,观察前后两个的变化与联系填就好了
为了写着省事用了第一种,但其实它复杂度高,推荐第二种
坑:
1.n=1 和 n=2 要特判
2.如果n>p,最后加的下取整的数为0,要特判,且特判的时候,注意长度不是【n-p】,p可能比2小,而我们矩阵的第一项是从F2 开始的,应为[n-max(2,p)]
3.矩阵快速幂三层循环的变量不要写错,。。一开始把第三层的k写成 i 死循环了
4.运算符重载后不要用scanf输入,在一些oj上会超时
5.max、min函数比较的是同一种变量
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> using namespace std; typedef long long ll; const int p=1e9+7; ll aa,b,c,d,mo,n; struct matrix { ll a[4][4]; ll* operator [](int x) {return a[x];}//这里是*不是& matrix operator *(matrix b)//重载*运算符 { matrix c; memset(c.a,0,sizeof(c.a)); ll tmp; for (int i=1;i<=3;i++) { tmp=0; for (int j=1;j<=3;c[i][j]=tmp%p,tmp=0,j++) for (int k=1;k<=3;k++) tmp+=(a[i][k]*b[k][j])%p; } //前提p^3不爆LL可以在第二层再取模 return c; } matrix operator ^(ll T) { matrix a=*this,b;//this是指针,所以是*this,这样才可以保证原来的a并不改变 memset(b.a,0,sizeof(b.a)); for (int i=1;i<=3;i++) b[i][i]=1; for (;T;a=a*a,T>>=1) if (T&1) b=b*a; return b; } }; matrix ans; void work(ll ci,ll chang){ ans[1][3]=chang; matrix node; node[1][1]=d,node[1][2]=1,node[1][3]=0; node[2][1]=c,node[2][2]=0,node[2][3]=0; node[3][1]=1,node[3][2]=0,node[3][3]=1; matrix ping=node^ci; ans=ans*ping; } int main(){ int t; scanf("%d",&t); for(int p=1;p<=t;p++){ cin>>aa>>b>>c>>d>>mo>>n; if(n==1){ cout<<aa;continue;//运算符重载后不要用scanf输入 } else if(n==2){ cout<<b;continue; } else{ ans[1][1]=b,ans[1][2]=aa; for(int i=1;i<=3;i++){ ans[2][i]=0;ans[3][i]=0; } for(ll i=3,j;i<=n;i=j+1){ if(mo/i==0)break; j=mo/(mo/i); if(n<j)j=n; work(j-i+1,mo/i); } ll w=2; if(mo>w)w=mo; if(n>mo)work(n-w,0);//一定不要直接用n-mo,如果mo是1会错误,要与2进行大小比较 cout<<ans[1][1]<<endl; } } return 0; }
再附上一个矩阵快速幂的板子:
struct matrix { int n,m; LL a[maxk][maxk]; LL* operator [](int x) {return a[x];}//这里是*不是& matrix operator *(matrix b) { int i,j,kk; matrix c; c.n=n,c.m=b.m; memset(c.a,0,sizeof(c.a)); LL tmp; for (i=1;i<=n;i++) for (j=1,tmp=0;j<=b.m;c[i][j]=tmp%p,tmp=0,j++) for (kk=1;kk<=m;kk++) tmp+=a[i][kk]*b[kk][j]; return c; } matrix operator ^(LL T) { matrix a=*this,b;//this是指针,所以是*this,这样才可以保证原来的a并不改变 memset(b.a,0,sizeof(b.a)); b.n=n,b.m=m; for (int i=1;i<=n;i++) b[i][i]=1; for (;T;a=a*a,T>>=1) if (T&1) b=b*a; return b; } }; /* ll* 返回的是指针,也就是 a[x]是一个指针(相当于返回第x行第0列的数值的指针),a[x][y]是一个数值,在外面调用a[x][y]时,相当于(m.a[x])[y]
F