【ybtoj】【RMQ问题】降雨量

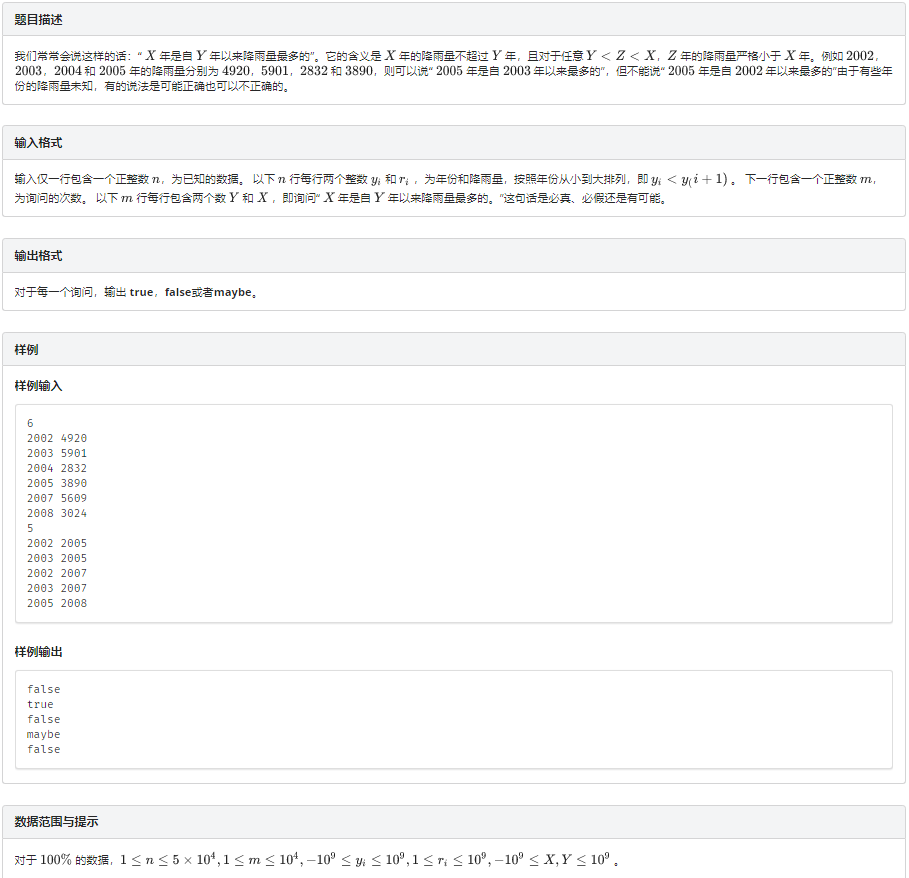
题意

题解

本题不难，就是多种情况分类讨论比较麻烦
一开始我的思路：(map)存下每一个已知年份的编号，对于两个不连续的年份，在中间加入一个降雨量为(-1)的年份表示不知道这个这中间中断的年份的降雨量
对于询问的([y,x])，查询对应编号的区间(num[mp_x]-1,num[mp_y]-1)中的最小值(看有没有(-1)),最大值(和两个端点的降雨量比较),然后...判断条件写炸了，(50pts)
正解思路：二分找到第一个大于等于(y)年份的已知年份(u)，第一个小于等于(x)年份的已知年份(v)，然后就是漫长的判断...
由于会很乱，所以最好分四种情况讨论:

• (x,y)已知,
• (x,y)未知
• (x)已知,(y)未知
• (x)未知,(y)已知
  注意几个容易忽视的细节：
• (x)未知,(y)已知的情况下，如果([u,v])中最大值(geq y)处的降雨量，那么输出(false)
• (x)已知,(y)未知的情况下，如果([u,v])中最大值(geq x)处的降雨量，那么输出(false)
  (具体的判断实在懒得打了，贴篇博客，内容复制在下面)

这里yea[i]表示第i个降雨量已知的年份，val[i]为第i个降雨量已知的年份的降雨量。
对于每一次询问，先求出从Y年开始往右查找最早能达到降雨量已知的年份编号u（之后的年份降雨量全部未知则为n+1），
如已知降雨量的年份分别为45 47 49 56 58 79，那么50年和56年对应的编号都是4（56在序列中的位置为4），
对于X年也求出往右查找最早能达到降雨量已知的年份编号v。由于年份是单调的，所以可用二分查找。
这样，求M年的降雨量是否已知，只需要先求出从M年开始往右查找最早能达到降雨量已知的年份编号s，
然后判断s != n + 1 && M == yea[s]。
分4种情况：
1、Y年和X年的降雨量都已知：
第一步，如果val[u] < val[v]，就说明不满足“X年的降雨量不超过Y年”这个条件，输出false并continue。
第二步，在v == u + 1的情况下，如果X == Y + 1就输出true（Y和X之间（不包括Y和X）没有整数）并continue，否则输出maybe并continue（Y和X之间存在降雨量未知的年份）。
第三步，查询[u + 1, v - 1]之间的最大值max（可用线段树或ST表维护），如果max >= val[v]，就说明不满足“对于任意
Y＜Z＜X，Z年的降雨量严格小于X年”这个条件，输出false并continue。
第四步，判断是否X - Y == v - u，如果为真就输出true（Y年和X年之间没有任何降雨量未知的年份），否则输出maybe（反之）。
2、Y年的降雨量未知，X年的降雨量已知：
第一步，如果u == v，输出maybe（Y年和X年之间年份的降雨量全部未知）并continue。
第二步，查询[u, v - 1]之间的最大值max，如果max >= val[v]，就说明不满足“对于任意Y＜Z＜X，Z年的降雨量严格小于X年”这个条件，输出false，否则输出maybe（Y年和X年的降雨量只要有一个未知就不能确定这句话是否一定为真）。
3、Y年的降雨量已知，X年的降雨量未知：
第一步，如果v == u + 1，输出maybe（Y年和X年的降雨量只要有一个未知就不能确定这句话是否一定为真）并continue。
第二步，查询[u + 1, v - 1]之间的最大值max，如果val[u] <= max，就说明X年的降雨量M不管为多少都无法同时满足M > max和 M <= val[u]，输出false，否则输出maybe（Y年和X年的降雨量只要有一个未知就不能确定这句话是否一定为真）。
4、Y年和X年的降雨量都未知：输出maybe（Y年和X年的降雨量只要有一个未知就不能确定这句话是否一定为真）。

代码

50pts

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 2e6+10;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
map<int,int> mp;
int n,y[N],r[N],dp[N][22],Log[N],tot,m,st[N][22];
struct id
{
	int y,r;
}num[N];
void buildst()
{
	for(int j=1;(1<<j)<=tot;j++)
		for(int i=1;i+(1<<j)-1<=tot;i++)
			dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]),
			st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);
	int k=0;
	for(int i=1;i<=tot;i++)	
	{
		if((1<<k)<=i) k++;
		Log[i]=k-1;
	}
}
inline int querymax(int l,int r)
{
	int k=Log[r-l+1];
	return max(dp[l][k],dp[r-(1<<k)+1][k]);
}
inline int querymin(int l,int r)
{
	int k=Log[r-l+1];
	return min(st[l][k],st[r-(1<<k)+1][k]);
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++) 
	{
		y[i]=read(),r[i]=read();
		if(i>1&&y[i]-y[i-1]>1) num[++tot]={y[i]-1,-1},mp[y[i]-1]=tot,dp[tot][0]=st[tot][0]=-1;
		num[++tot]=(id){y[i],r[i]},mp[y[i]]=tot,dp[tot][0]=st[tot][0]=r[i];
	
	}
	m=read();
	buildst();
	for(int i=1;i<=m;i++)
	{
		int ya=read(),xa=read();
		int maxn=querymax(mp[ya]+1,mp[xa]-1),
			minn=querymin(mp[ya]+1,mp[xa]-1);
	//	printf("(%d,%d):maxn=%d
",mp[ya]+1,mp[xa]-1,maxn);
	//	printf("rain:(x,y):[%d,%d]
",num[mp[xa]].r,num[mp[ya]].r);
		if( (num[mp[xa]].r==-1||num[mp[xa]].r==0)&&(maxn<=num[mp[ya]].r||num[mp[ya]].r==0||num[mp[ya]].r==-1)) 
			{printf("maybe
");continue;} 
		if((maxn>=num[mp[xa]].r&&num[mp[xa]].r!=-1&&num[mp[xa]].r!=0)||
		(num[mp[ya]].r!=-1&&num[mp[ya]].r!=0&&num[mp[xa]].r!=-1&&num[mp[xa]].r!=0&&num[mp[ya]].r<num[mp[xa]].r)) 
			{printf("false
");continue;}
		if(num[mp[ya]].r==-1||num[mp[ya]].r==0||minn==-1)  
			printf("maybe
");
		else printf("true
");
	
		
			
	}
	return 0;
}
/*
8
-8 1
-2 2
0 6
1 5
2 7
13 1
18 10
19 14
4
-19 -2
-2 -1
-18 -2
8 12
*/

100pts

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
using namespace std;
map<int,int> id;
int n,st[50001][16],a_id[50001];
int findL(int L){
    int mid,l = 1,r = n + 1;
    while(l < r){
        mid = (l + r) >> 1;
        if(a_id[mid] >= L) r = mid;
        else l = mid + 1;
    }
    return l;
}
int findR(int R){
    int mid,l = 0,r = n;
    while(l < r){
        mid = (l + r + 1) >> 1;
        if(a_id[mid] > R) r = mid - 1;
        else l = mid;
    }
    return l;
}
int main(){
    int i,j,q,y,l,r,templ,tempr,L,R,len,res,Log[50001];
    scanf("%d",&n);
    for(i = 1;i <= n;i++){
        scanf("%d %d",&a_id[i],&y);
        id[a_id[i]] = i,st[i][0] = y;
    }
    Log[0] = -1;
    for(i = 1;i <= n;i++) Log[i] = Log[i >> 1] + 1;
    for(j = 1;j <= Log[n];j++){
        for(i = 1;i + (1 << j) - 1 <= n;i++){
            st[i][j] = max(st[i][j - 1],st[i + (1 << (j - 1))][j - 1]);
        }
    }
    scanf("%d",&q);
    for(i = 1;i <= q;i++){
        scanf("%d %d",&L,&R);
        if(R <= L){
            printf("false
");
            continue;
        }
        l = findL(L),r = findR(R);
        templ = l + 1,tempr = r - 1;
        if(!id[R]) ++tempr;
        if(!id[L]) --templ;
        len = Log[tempr - templ + 1];
        //aprintf("%d %d %d %d %d
",l,r,templ,tempr,len);
        if(id[L] && id[R] && st[l][0] < st[r][0]){
        	printf("false
");	
        	continue;
		}
        res = max(st[templ][len],st[tempr - (1 << len) + 1][len]);
        //printf("%d %d %d
",res,st[templ][len],st[tempr - (1 << len) + 1][len]);
        if((id[L] && res >= st[l][0]) || (id[R] && res >= st[r][0])) printf("false
");
        else{
            if(id[R] - id[L] != R - L || !id[R] || !id[L]) printf("maybe
");
            else printf("true
");
        }
    }
    return 0;
}
/*
8
-8 1
-2 2
0 62
1 5
2 7
13 1
18 10
19 14
6
-19 -2
-2 -1
-18 -2
8 12
1 2
2 13
*/