【ybtoj】【背包问题】魔法开锁

题意

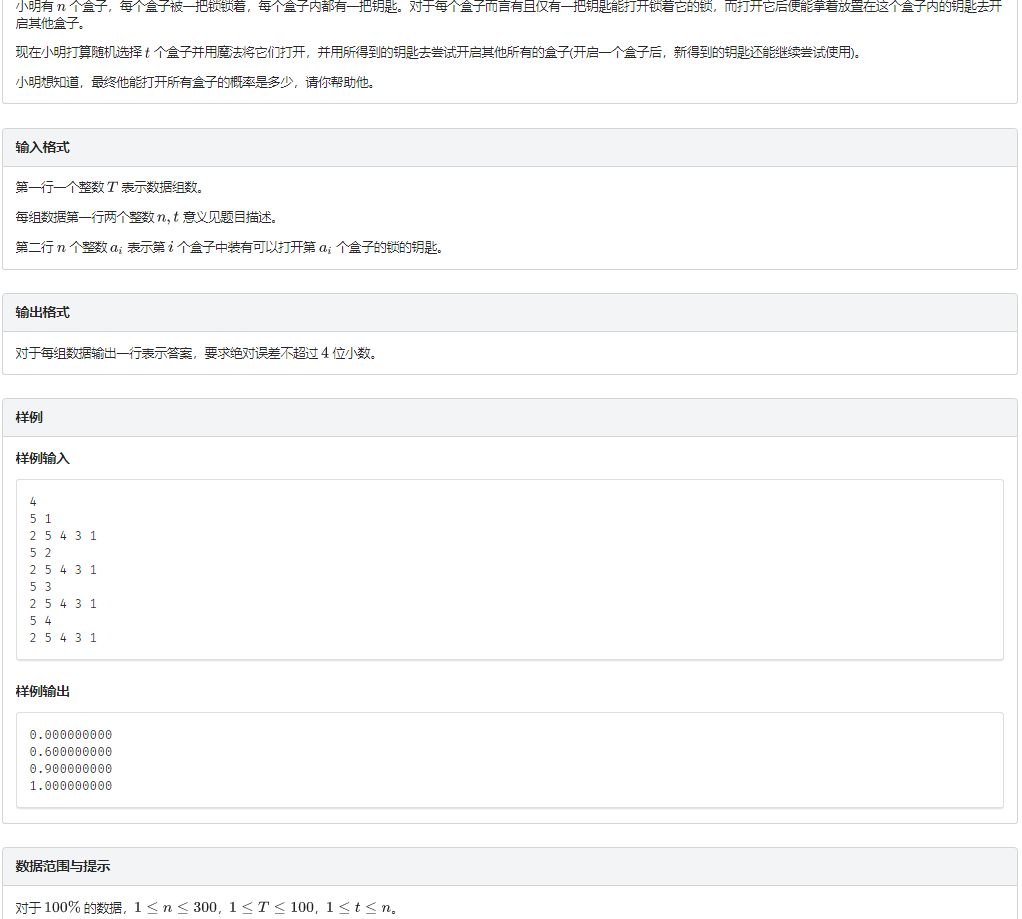
题解

此题坑还是很大的。

一开始看到题目所说概率云云，联想到的是类似期望DP之类的方法，苦思冥想之后放弃，几乎没有思路

首先需要转化问题：求出“选出 t 个点覆盖掉所有的环”的方案数和所有选择的方案数（也就是从 n 个点中选 t 个点，即C(n,m)）

那么我们先预处理出组合数的递推

void init()
{
	c[0][0]=1;
	for(int i=1;i<=300;i++)	
	{
		c[i][0]=1;
		for(int j=1;j<=i;j++) 
			c[i][j]=c[i-1][j]+c[i-1][j-1];
	}
}

再找到所有的环并求出其大小

for(int i=1;i<=n;i++)
{
	if(!vis[i]) 
	{
		int now=i,tot=0;
		while(1)
		{
			if(vis[now]) break;
			vis[now]=1,tot++;
			now=a[now];
		}
		cir[++cnt]=tot;
	}
}

设计 dp[i][[j]表示前 i 个环里选了 j 个点的方案数，就可以写出类似背包的转移：dp[i][j]+=dp[i-1][k]*c[cir[i]][j-k] (cir表示环的大小）

注意转移时的边界 0<=k<j，因为每个环都至少选一个点

	dp[0][0]=1;
	for(int i=1;i<=cnt;i++)
		for(int j=0;j<=t;j++)
			for(int k=0;k<j;k++)
				dp[i][j]+=dp[i-1][k]*c[cir[i]][j-k];
	

Tips：虽然只有最后一步除法求概率用到了double，但是 dp，c 等数组都要开成double。因为组合数范围比较大，所以会爆 long long，而double的上界是10³⁰⁸，可以通过

完整代码

点击查看代码

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define db double 
const int INF = 0x3f3f3f3f,N = 305;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
db a[N],c[N][N],dp[N][N];
ll cnt,cir[N],T,n,t;
bool vis[N];
void init()
{
	c[0][0]=1;
	for(int i=1;i<=300;i++)	
	{
		c[i][0]=1;
		for(int j=1;j<=i;j++) 
			c[i][j]=c[i-1][j]+c[i-1][j-1];
	}
}
void solve()
{
	memset(vis,0,sizeof(vis));
	memset(cir,0,sizeof(cir));
	memset(dp,0,sizeof(dp));
	cnt=0;
	n=read(),t=read();
	for(int i=1;i<=n;i++) a[i]=read();
	for(int i=1;i<=n;i++)
	{
		if(!vis[i]) 
		{
			int now=i,tot=0;
			while(1)
			{
				if(vis[now]) break;
				vis[now]=1,tot++;
				now=a[now];
			}
			cir[++cnt]=tot;
		}
	}
	dp[0][0]=1;
	for(int i=1;i<=cnt;i++)
		for(int j=0;j<=t;j++)
			for(int k=0;k<j;k++)
				dp[i][j]+=dp[i-1][k]*c[cir[i]][j-k];
	
	printf("%.9lf
",1.0*dp[cnt][t]/c[n][t]);
}
int main()
{
	T=read();
	init();
	while(T--) solve();
	return 0;
}