题意
(颜色表示难度)
T1
(cubicp)立方数
给定质数pp,求是否满足∃a,b∃a,b,使得p=a3−b3。
T2
(dp)动态规划
给定长度为nn序列,分成kk段,求每段相同数字对数的最小和。
T3
(number)游戏
有nn个数字和TT次给定询问,每次询问给定[l,r][l,r]的最小值xx,求第几次操作是矛盾的。
解题报告
T1
一个P数如果是立方差数,不妨假设是x^3-y^3(x>y)。相当于(x-y)(x^2+xy+y^2),由于P是质数,因此x=y+1。又有(x-1)^2+x^2+x(x-1)=P,暴力枚举1~10^6判断即可。
T2
令dp[i][ j]表示前i个数分成j段的最少价值。枚举这个断点k,有dp[i][ j]=min{dp[k][ j-1]+sum(k+1,i)}。(事实上这个k具有单调性,用经典的1D1D动态规划优化即可。)
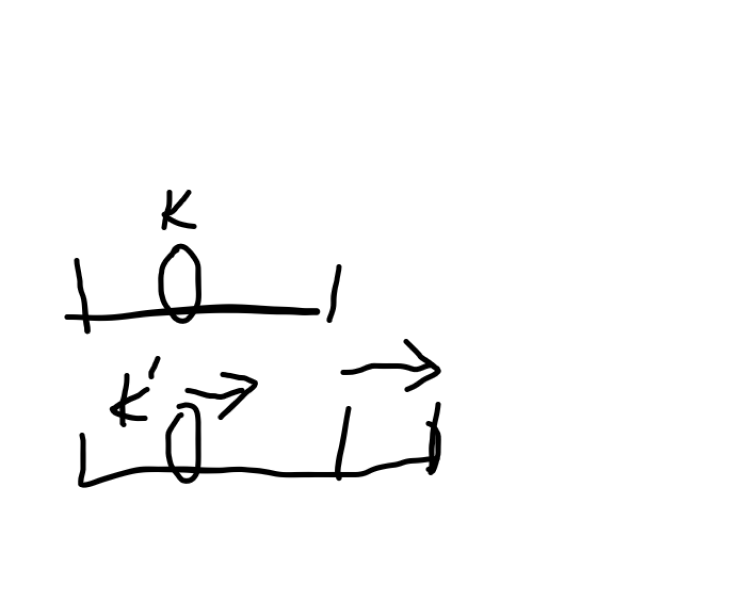
这里转移就涉及到决策单调性,简单来说就是这样一个图,原本决策点在k,当区间向右延展之后决策点k’只可能向右移动或者不动,不可能向左移动,这就是所谓的满足决策单调性。
T3
方法1:
对于所有区间最小值为x的操作的区间交只有一种情况会出现矛盾:对于最小值超过x的区间的并包含该区间交。因此我们可以二分答案,之后将所有最小值从大到小进行排序,利用并查集维护即可。
方法2:
判断矛盾的思路同方法1,也可以用线段树初始把所有位置设置为1,每次从大到小更改区间最小值的时候把区间内全部清0,如果访问的区间和为0(即区间内全部为0),就说明矛盾
赛时代码
T1-cubicp立方数(60->100)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e4+10;
ll a[N],sum[N];
void init()
{
for(int i=1;i<=N;i++)
a[i]=i*i*i;
// for(int i=1;i<=N;i++)
// sum[i]=a[i]-a[i-1];
}
bool check()
{
ll p;
scanf("%lld",&p);
ll n=min((ll)(upper_bound(sum+1,sum+N+1,p)-sum),(ll)N);
for(int i=1;i<=n;i++)
for(int j=1;j<i;j++)
if(a[i]-a[j]==p) return 1;
return 0;
}
ll calc(ll x)
{
return 3*x*x+3*x+1;
}
bool judge()
{
ll p;
scanf("%lld",&p);
int l=1,r=1e6+10;
while(l<r)
{
int mid=(l+r)>>1;
if(calc(mid)<p) l=mid+1;
else r=mid;
}
while(l<r)
{
int mid=(l+r)>>1;
if(calc(mid)<=p) l=mid;
else r=mid-1;
}
return calc(l)==p;
}
int main()
{
// freopen("cubicp.in","r",stdin);
// freopen("cubicp.out","w",stdout);
init();
int T;
scanf("%d",&T);
while(T--)
{
if(judge()) printf("YES
");
else printf("NO
");
}
return 0;
}T2-dp动态规划(40)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e3+10,INF = 0x3f3f3f3f;
int n,K;
int a[N];
ll dp[N][N][25];
ll sum[N][N];
ll jc(ll x){return x*(x-1)/2;}
ll calc(int l,int r)
{
ll ans=0;
for(int i = 1 ; i <= n ; i ++)
{
if(sum[r][i] != sum[l-1][i])
ans+=jc(sum[r][i]-sum[l-1][i]);
}
//printf("(%d,%d):%lld
",l,r,ans);
return ans;
}
ll solve(int l,int r,int k)
{
// printf("checking[%d][%d][%d]
",l,r,k);
if(dp[l][r][k]) return dp[l][r][k];
if(k == 1)
{ //printf(":dp[%d][%d][%d]=%lld
",l,r,k,calc(l,r));
return dp[l][r][k]=calc(l,r);
}
dp[l][r][k]=INF;
for(int i=l;i<r;i++)
for(int j=1;j<k;j++)
{
if(i-l+1>=j&&r-i+1>=k-j)
dp[l][r][k]=min(dp[l][r][k],solve(l,i,j)+solve(i+1,r,k-j));
}
// printf("dp[%d][%d][%d]=%lld
",l,r,k,dp[l][r][k]);
return dp[l][r][k];
}
int main()
{
//freopen("dp.in","r",stdin);
//freopen("dp.out","w",stdout);
scanf("%d%d",&n,&K);
bool flag=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
if(i>1&&a[i]!=a[i-1]) flag=1;
}
// if(!flag)
// {
// ll res=0;
// if(n%K==0)
// {
// res+=K*(jc(n/K));
// printf("%lld",res);
// }
// else
// {
// res+=(K-1)*(jc(n/K));
// res+=jc(n/K+n%K);
// printf("%lld",res);
// }
// return 0;
// }
for(int i=1;i<=n;i++)
{
sum[i][a[i]]=sum[i-1][a[i]]+1;
for(int j=1;j<=n;j++)
if(j!=a[i]) sum[i][j]=sum[i-1][j];
}
// for(int j = 1 ; j <= 2 ; j ++)
// for(int i = 1 ; i <= n ; i ++)
// printf("%d,%d:%lld
",i,j,sum[i][j]);
printf("%lld",solve(1,n,K));
return 0;
}
/*
10 2
1 2 1 2 1 2 1 2 1 2
*/T3-number游戏(70)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int read()
{
int a = 0,x = 1;char ch = getchar();
while(ch > '9' || ch < '0') {if(ch == '-') x = -1;ch = getchar();}
while(ch >= '0' && ch <= '9') {a = a*10 + ch-'0';ch = getchar();}
return a*x;
}
const int N = 1005;
int l[N], r[N];
int main()
{
freopen("number.in", "r", stdin);
freopen("number.out", "w", stdout);
int n, k;
scanf("%d%d", &n, &k);
int ans;
for (ans=1;ans<=k;ans++)
{
int a,b,c;
a=read(),b=read(),c=read();
if (l[c]==0||r[c]==0)
l[c]=a, r[c]=b;
else
{
if (a>r[c]||b<l[c])
break;
if (a>l[c])
l[c]=a;
if (b<r[c])
r[c]=b;
}
for (int i=1;i<c;i++)
{
if (l[i]&&r[i]&&r[i]<=r[c]&&l[i]>=l[c])
{
printf("%d",ans);
return 0;
}
}
for (int i=c+1;i<=n;i++)
{
if (l[i]&&r[i]&&r[i]>=r[c]&&l[i]<=l[c])
{
printf("%d",ans);
return 0;
}
}
}
printf("%d", ans);
}
/*
20 5
1 10 4
1 5 4
5 6 6
6 10 6
4 5 5
*/STD标答
T1
点击查看代码
#include <iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<map>
#include<set>
#include<string>
using namespace std;
int main()
{
freopen("cubicp.in","r",stdin);
freopen("cubicp.out","w",stdout);
int t,flag;
scanf("%d",&t);
long long p;
while(t--)
{
flag=0;
scanf("%I64d",&p);
for(int i=1;i<=1e6+10;i++)
{
if(3ll*i*i+3*i+1==p)
{
flag=1;
break;
}
if (3ll*i*i+3*i+1>p) break;
}
if(flag) printf("YES
");
else printf("NO
");
}
return 0;
}T2
点击查看代码
#include<iostream>
#include<cstdio>
using namespace std;
const int N=100010;
typedef long long LL;
int c[N],a[N];
LL f[N],g[N];
int p,q,n,k;
LL tot;
void move(int l,int r)
{
while (l<p) p--,tot+=c[a[p]],c[a[p]]++;
while (r>q) q++,tot+=c[a[q]],c[a[q]]++;
while (p<l) c[a[p]]--,tot-=c[a[p]],p++;
while (r<q) c[a[q]]--,tot-=c[a[q]],q--;
}
void work(int l,int r,int fl,int fr)
{
if (fl>fr) return;
int mid=(fl+fr)>>1,mi;
LL mx=1LL<<60;
for (int i=l;i<=r;i++)
if (i<mid)
{
move(i+1,mid);
if (f[i]+tot<mx) mx=f[i]+tot,mi=i;
}
g[mid]=mx;
work(l,mi,fl,mid-1);
work(mi,r,mid+1,fr);
}
int main()
{
freopen("dp.in","r",stdin);
freopen("dp.out","w",stdout);
scanf("%d%d",&n,&k);
for (int i=1;i<=n;i++) scanf("%d",&a[i]);
f[0]=0;
for (int i=1;i<=n;i++) f[i]=1LL<<60;
while (k--)
{
p=1,q=0,tot=0;
for (int i=1;i<=n;i++) c[i]=0;
work(0,n-1,1,n);
for (int i=0;i<=n;i++) f[i]=g[i],g[i]=0;
}
cout<<f[n];
return 0;
}T3
点击查看代码
#include <cstdio>
#include <iostream>
#include <algorithm>
#define N 1000011
#define min(x, y) ((x) < (y) ? (x) : (y))
#define max(x, y) ((x) > (y) ? (x) : (y))
using namespace std;
int n, q, ans;
int f[N];
struct node
{
int x, y, z;
}p[N], t[N];
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = -1;
for(; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
return x * f;
}
inline bool cmp(node x, node y)
{
return x.z > y.z;
}
inline int find(int x)
{
return x == f[x] ? x : f[x] = find(f[x]);
}
inline bool check(int k)
{
int i, j, x, y, lmin, lmax, rmin, rmax;
for(i = 1; i <= n + 1; i++) f[i] = i;
for(i = 1; i <= k; i++) t[i] = p[i];
std::sort(t + 1, t + k + 1, cmp);
lmin = lmax = t[1].x;
rmin = rmax = t[1].y;
for(i = 2; i <= k; i++)
{
if(t[i].z < t[i - 1].z)
{
if(find(lmax) > rmin) return 1;
for(j = find(lmin); j <= rmax; j++)
f[find(j)] = find(rmax + 1);
lmin = lmax = t[i].x;
rmin = rmax = t[i].y;
}
else
{
lmin = min(lmin, t[i].x);
lmax = max(lmax, t[i].x);
rmin = min(rmin, t[i].y);
rmax = max(rmax, t[i].y);
if(lmax > rmin) return 1;
}
}
// cout<<find(1)<<endl;
if(find(lmax) > rmin) return 1;
return 0;
}
int main()
{
freopen("number.in","r",stdin);
freopen("number.out","w",stdout);
int i, x, y, mid;
n = read();
q = read();
for(i = 1; i <= q; i++)
p[i].x = read(), p[i].y = read(), p[i].z = read();
x = 1, y = q;
//cout<<check(2)<<endl;
//return 0;
while(x <= y)
{
mid = (x + y) >> 1;
if(check(mid)) ans = mid, y = mid - 1;
else x = mid + 1;
}
printf("%d
", ans);
return 0;
}