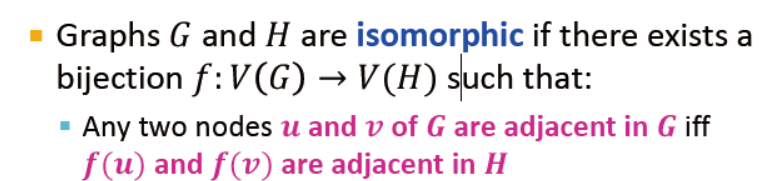Motifs and Structure Roles in Networks
子图/子网络：subnetworks→network中的组成部分，可用于描述网络特性或区分网络
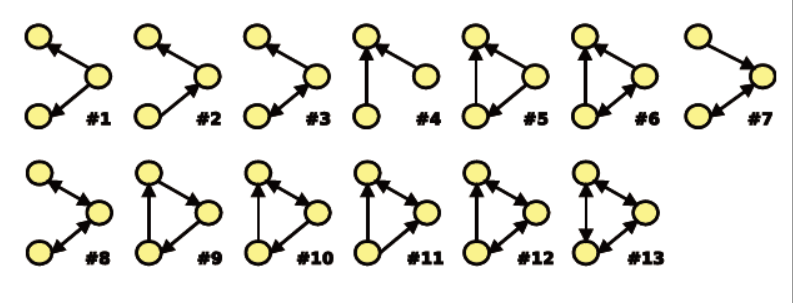
例子：3个节点的有向子图的不同形态
对于每一个subgraph：
假设我们有一度量工具可以用于对subgraph的重要性（显著性？）进行评估：
负值表示under-representation （不能很好的表征,欠表征？）
正值表示over-representation （过表征？）
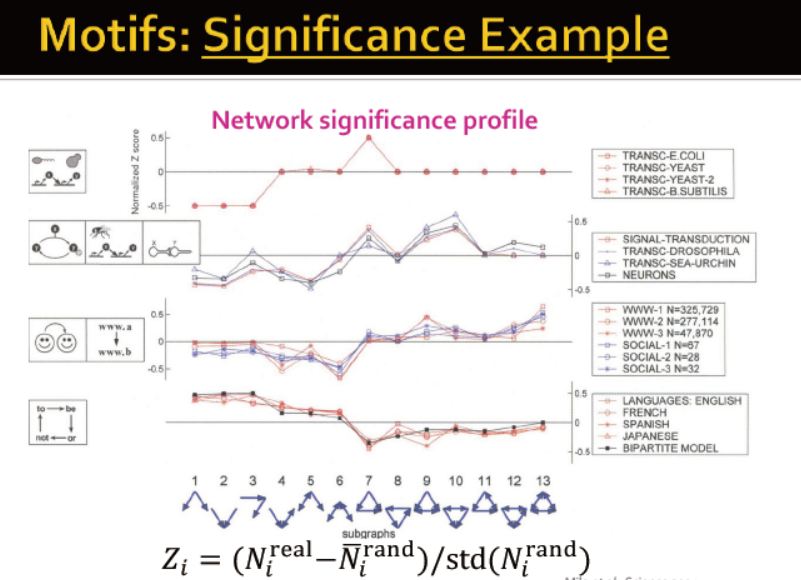
定义网络重要性（显著性？）（network significance profile）：一个特征向量，向量中的元素值为所有子图的类型
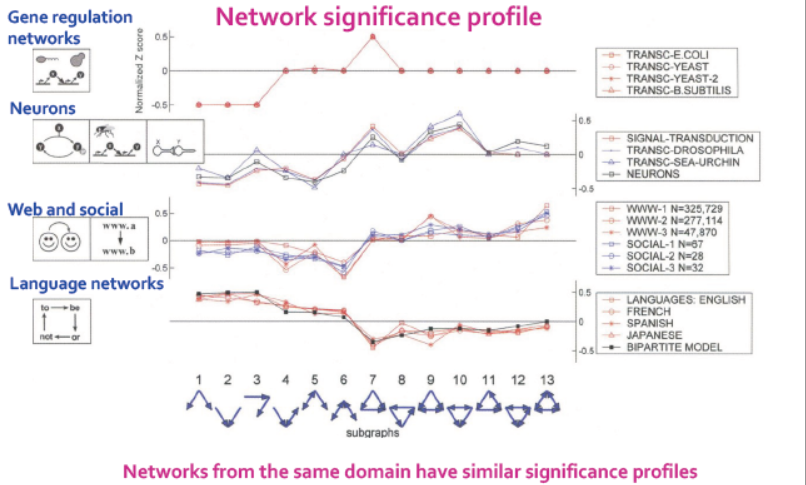
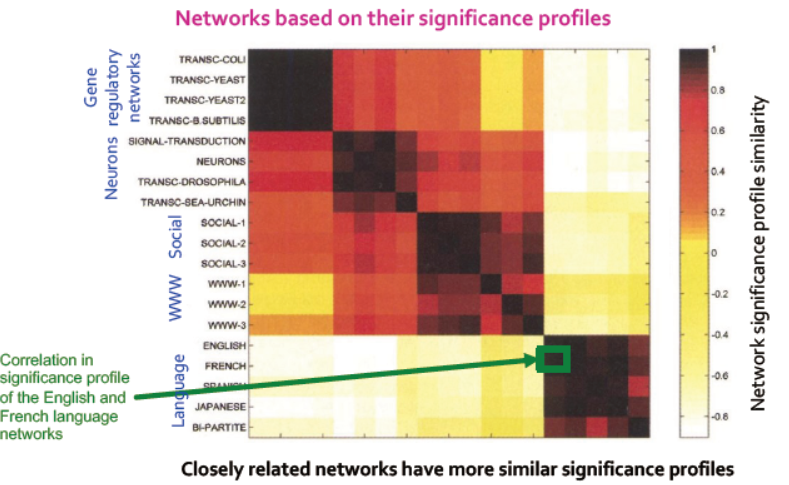
那么，接下来，我们需要比较不同网络的profiles：
从下图中，横轴是不同的子图类型，纵轴是归一化后的z score( 应该是指重要度，但此处未给出重要度是如何计算出来的)。不同的曲线表示同类网络中的不同地域/应用。由曲线可得，同类网络具备相似的significance profiles
因此，今天的任务：
1）子图： 定义及发现motifs和graphlet；
2）网络的结构角色：RolX: Structural Role Discovery Method 发现工具
3）发现Structural Role以及其的应用：结构相似度；角色生成与迁移学习；Making sense of roles
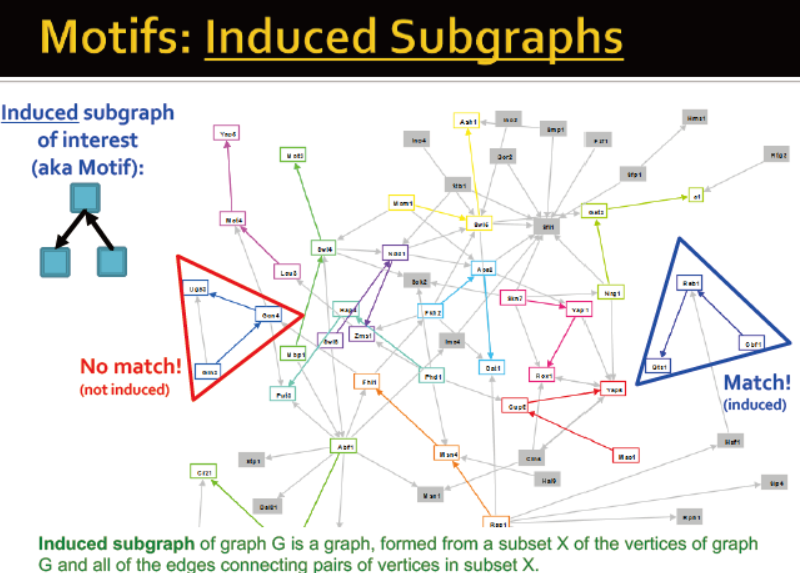
subgraph， motifs 和 graphlet
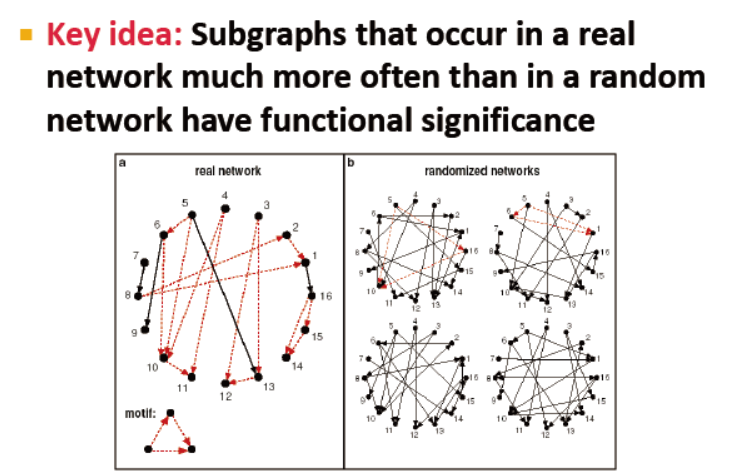
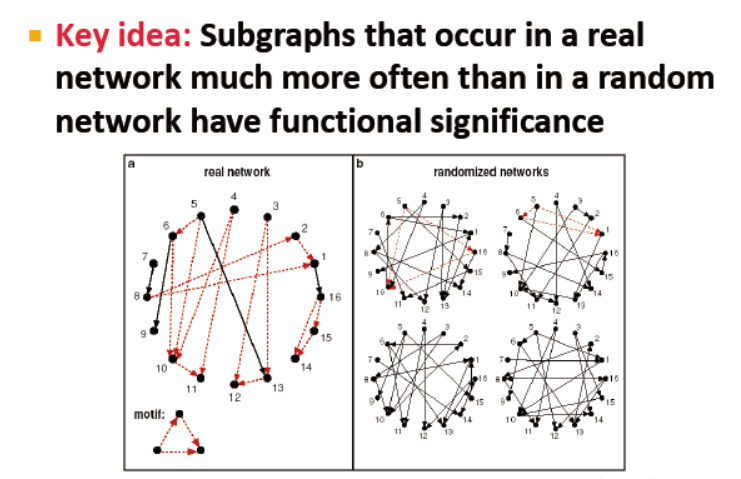
首先来看 network motifs：recurring, significant patterns of interconnections 重复出现的，具有显著意义的连接模式
pattern：小型的，具备说服力的子图
recurring：出现多次，高频出现
significant：比预期更频繁？？
为什么我们需要motifs：
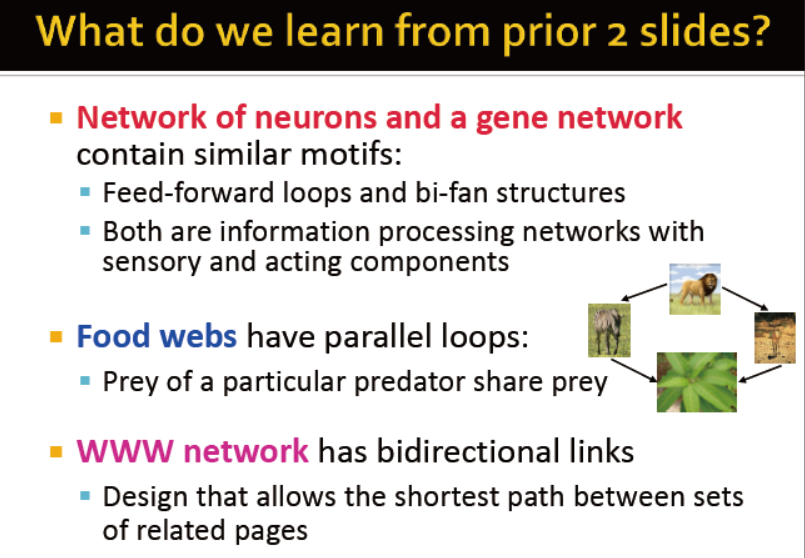
1. 帮助我们更好的认识网络
2. 帮助我们更好的预测在给定场景下的网络的操作与反应
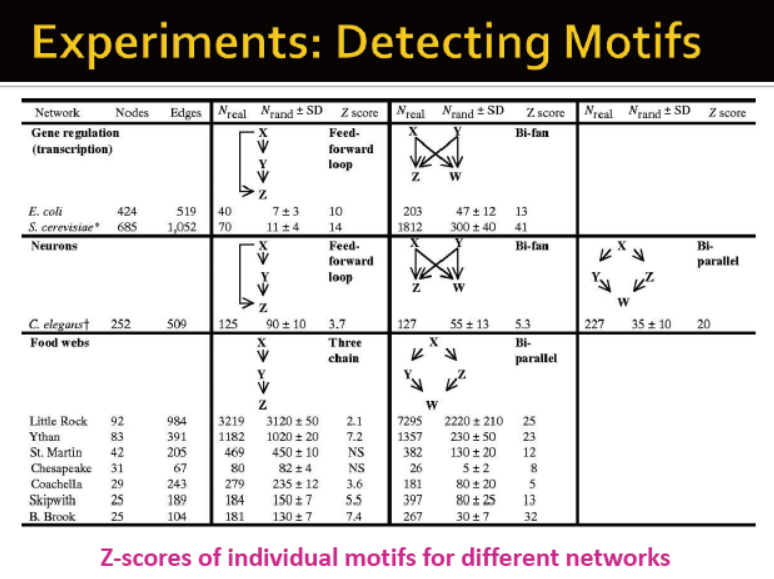
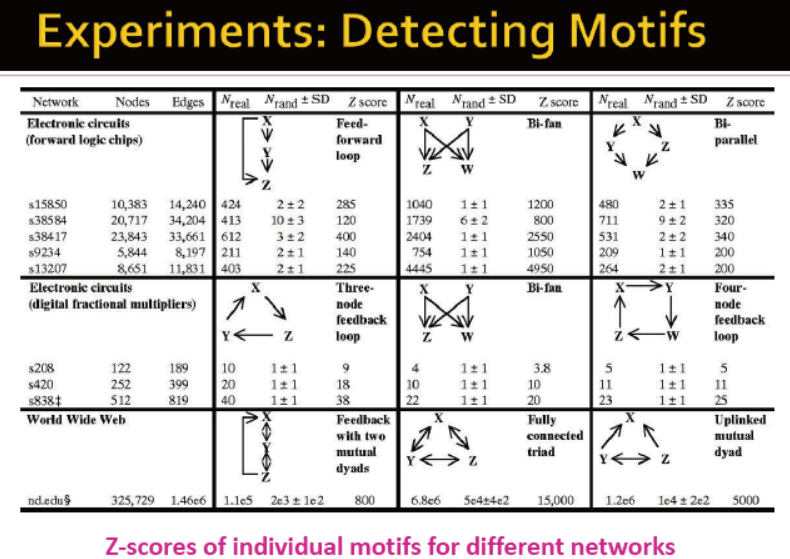
例如：
feed-forward loops： 在神经元网络中出现，应用于消除生物噪音？
parallel loops：食物网络中
single-input modules：基因控制网
motifs：子图的匹配与导出
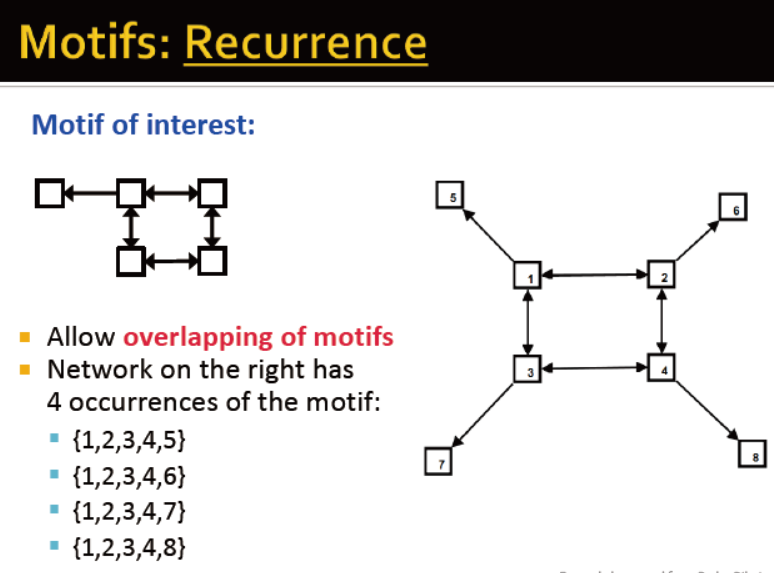
motifs：重复出现 下图中，左边的网络出现了4次左上角的子图类型
子图的意义： 现实网络比 随机网络中出现得较多的子图，具备功能的重要性
motif的重要意义：当网络与随机网络比较时，motif可用于表征网络
zi==motif i 的统计显著性 （#（**）表示什么？？）
网络的显著性 sp
sp是一组正则化后的z-score的向量
sp强调子图的关联显著性：用于比较不同size网络；一般来说，越大的网络，z-score越高
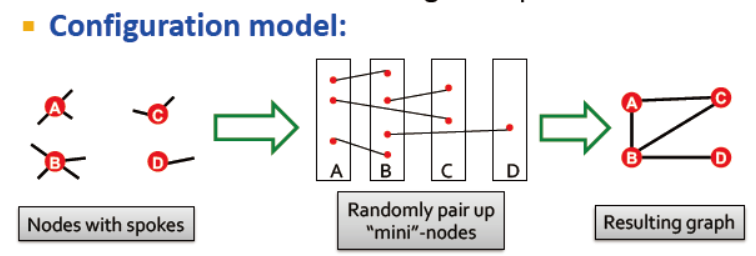
Configuration Model：
目标：基于给定的度序列 k1,k2,...,kn 生成一个随机图
可用于比较具有相同度序列的随机图与真实图
给定的辐射节点，随机组队，生成图
Alternative for spokes： switching
选节点，交换边的端点，多次重复？？
一开始介绍motif时的那个图
发现/检测 motifs
1. 计数真实图中的子图
2. 统计随机图中的子图 （可能有多个随机图）
3. 计算z-score
4. z-score越高的子图，月可能是图的motif
motif概念的变种：
规范定义：有向及无向；着色与未着色；变化与静态
概念的变种：不同频率概念；不同的显著性度量；欠表征？；null model 的不同约束
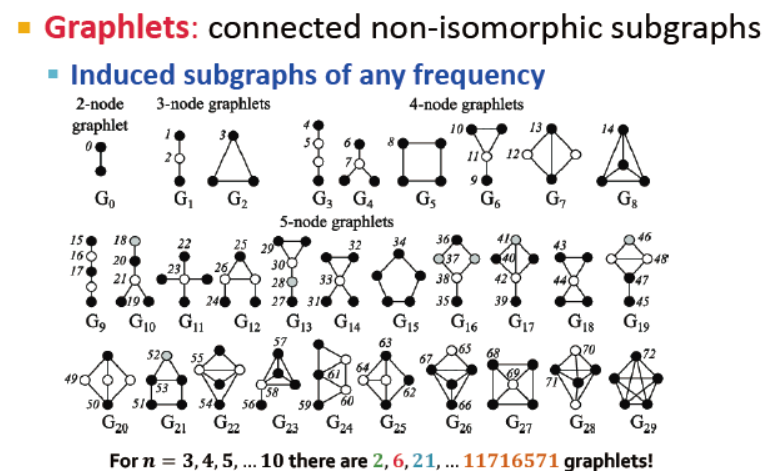
Graphlets： node feature vectors 节点特征向量
Graphlets：连接的非同构子图
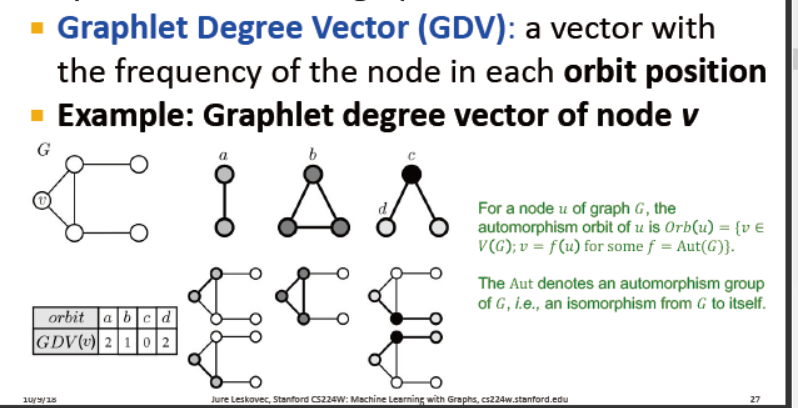
graphlet的度向量
使用graphlet来获取一个节点级别的子图度量
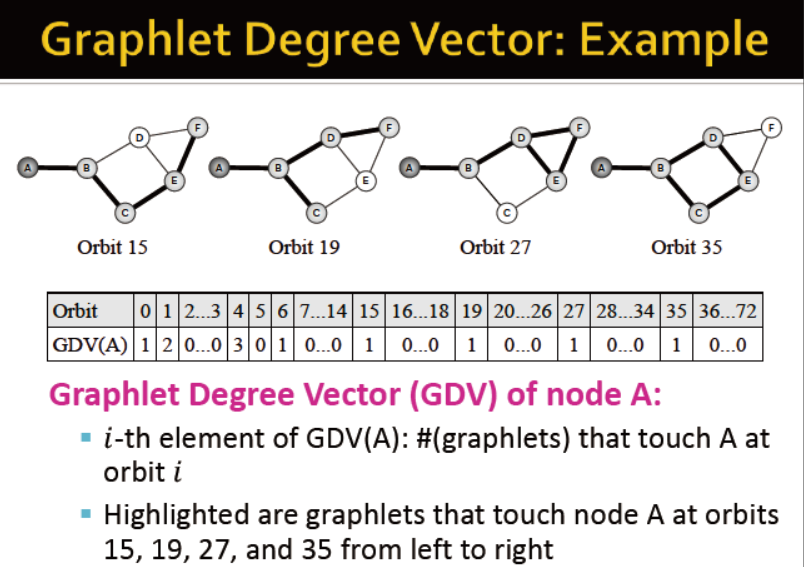
graphlet degree vector 对一个节点接触的graphlet的计数
automorphism orbit：自同构轨迹？ 考虑子图的对称性
graphlet degree vector （GDV）：
若只考虑2到5节点的graphlet，那么73维向量可以表示节点的邻居拓扑，即最多捕捉4跳的距离
GDV是衡量节点局部网络拓扑的工具，可用于比较两个节点的相似度
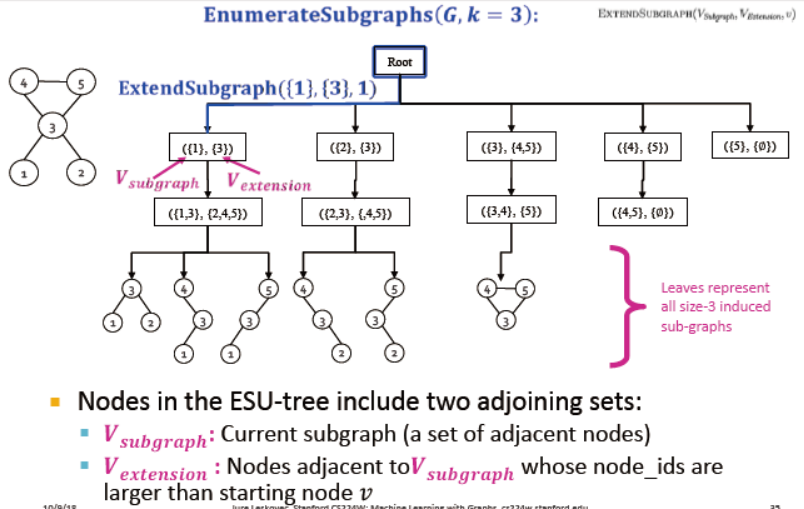
Finding motifs and graphlets
寻找k-size的motifs或graphlet，需要解决两个问题：
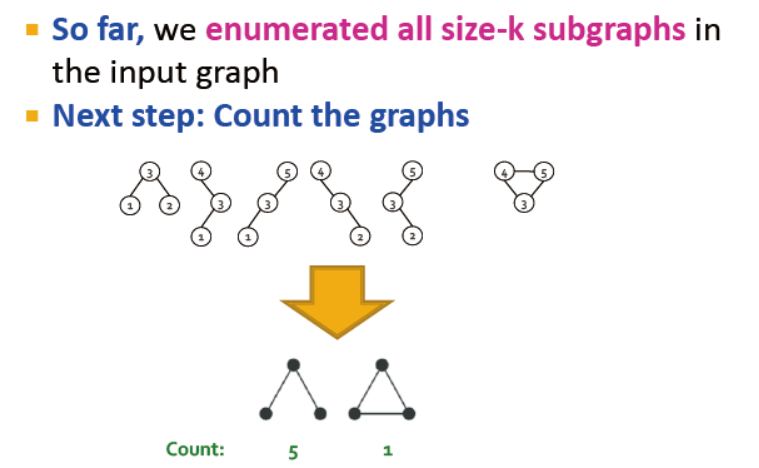
1. 枚举所有样式的size-k的连接子图
2. 计数
但是，确定一个网络中是否包含包含某一子图，是难以计算的
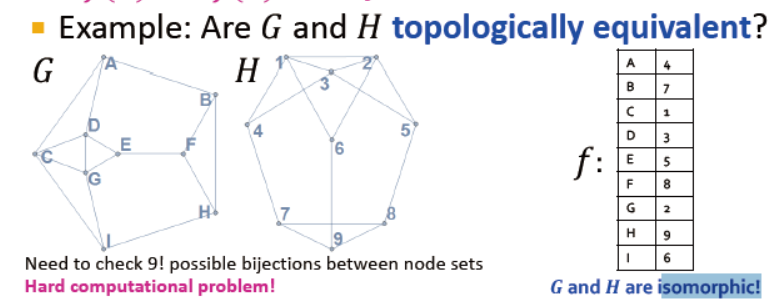
图同构：
图G,H是同构的，那么存在一个双射f：V(G）→V（H），使
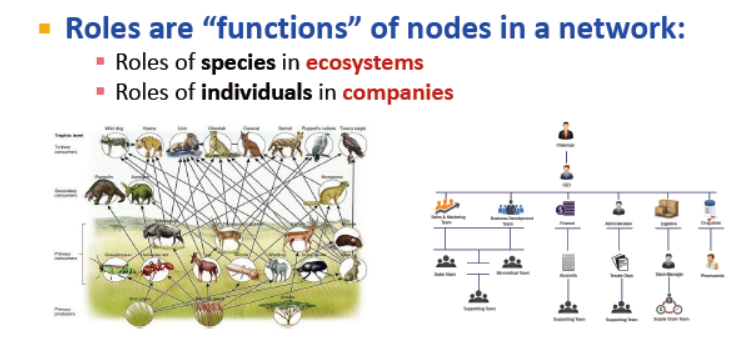
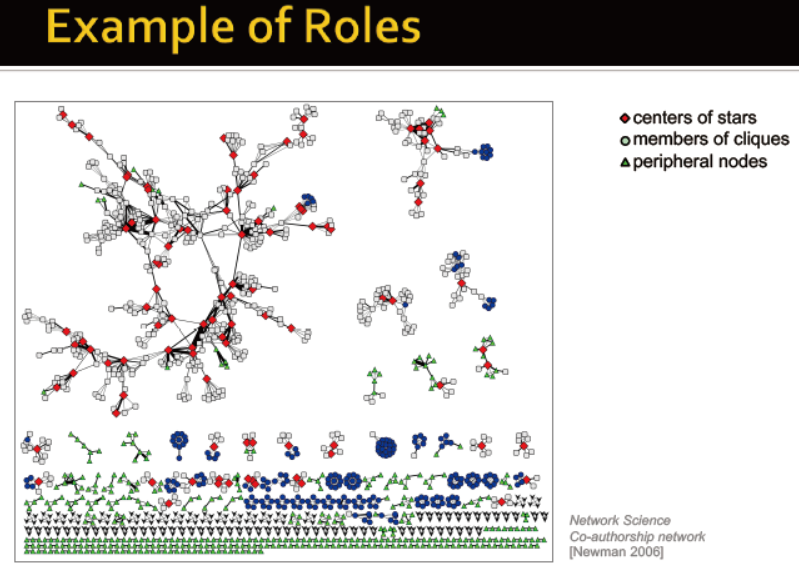
网络中的结构角色
角色有结构中的行为来衡量：
中心点，团的成员，外围节点
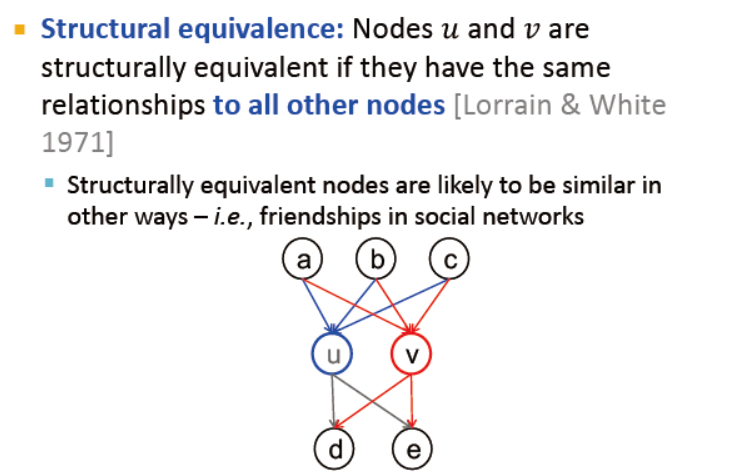
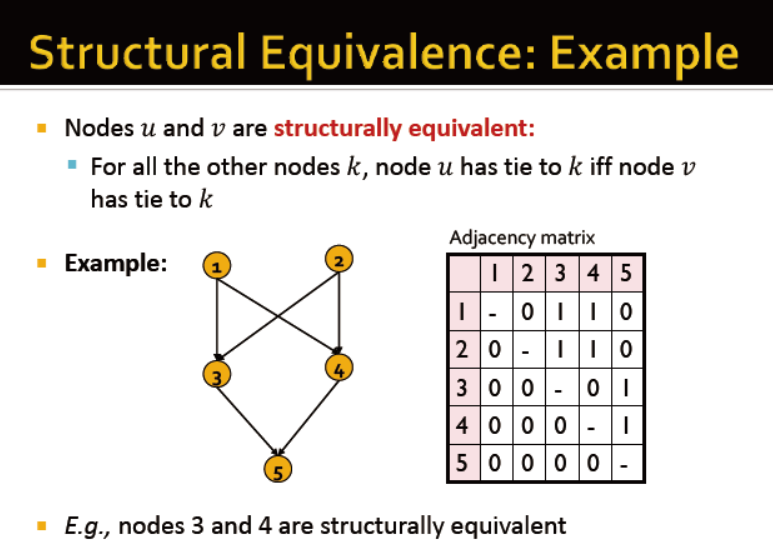
结构等效节点：
探索网络中的结构角色
角色查询：识别相似个体
角色动态变化：识别行为变化
角色转移：使用一个网络中的已知来预测另一网络
网络比较：比较网络相似性
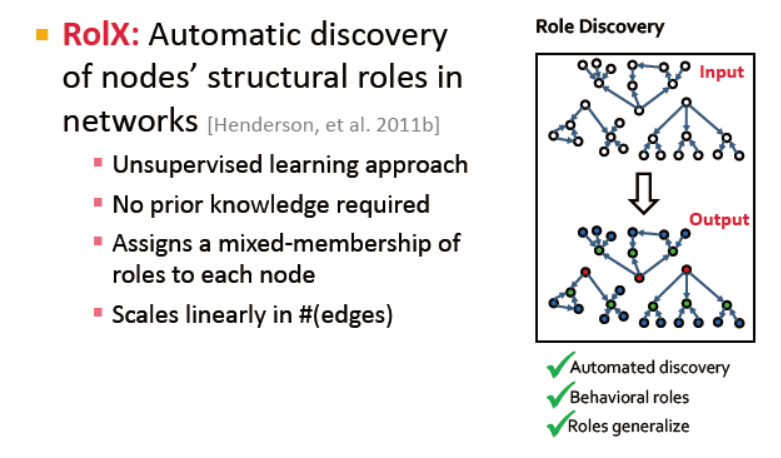
RoIX： 在网络洛自动发现节点角色
无监督学习，无需先验知识，可发现节点的混合角色，边数的先行拓展？
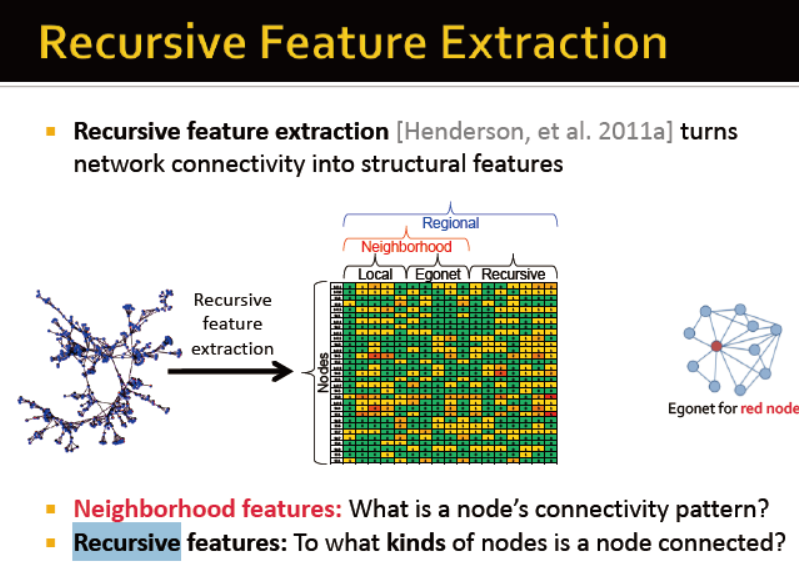
Recursive feature extraction ：将网络连接性转化为解雇特征
neighborhood feature：节点的连接模式
recursive features：一个节点连接到什么类型的节点
local features：节点度的度量。若为有向图，包含出度，入度，总度；若为带权重的图，则包含权重向量
egonet features：计算节点的egonet（自我网络？）
egonet包含：节点，邻居，边
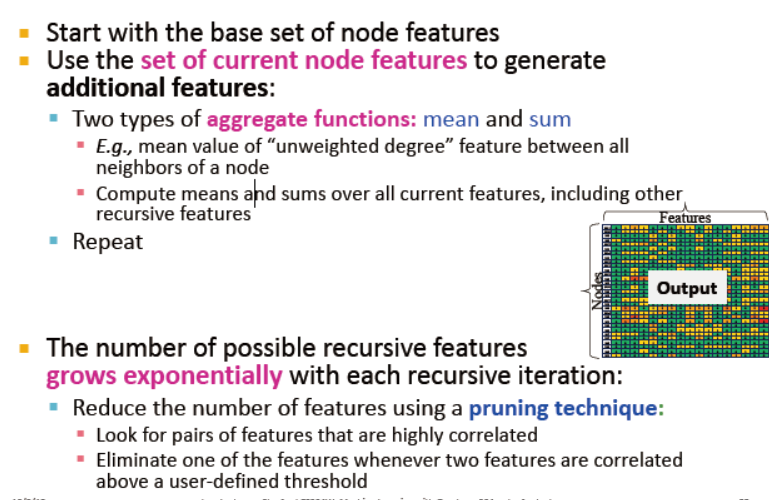
此外，还增加平均和最大这两个统计特征
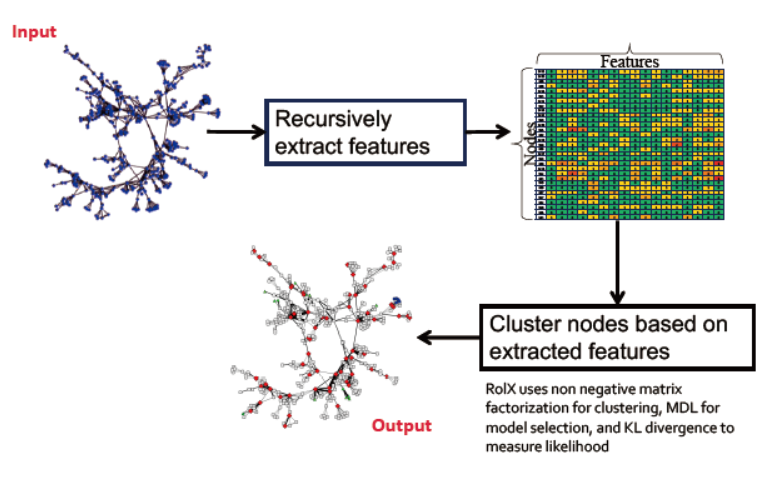
RoIx：使用 non negative matrix factorization 用于聚类，MDL（最小描述长度？）用于模型选择，KL散度用于相似度衡量
应用：结构相似度
将节点基于他们的结构相似度进行聚类：
通过RoIx获取节点的向量
向量进行聚类
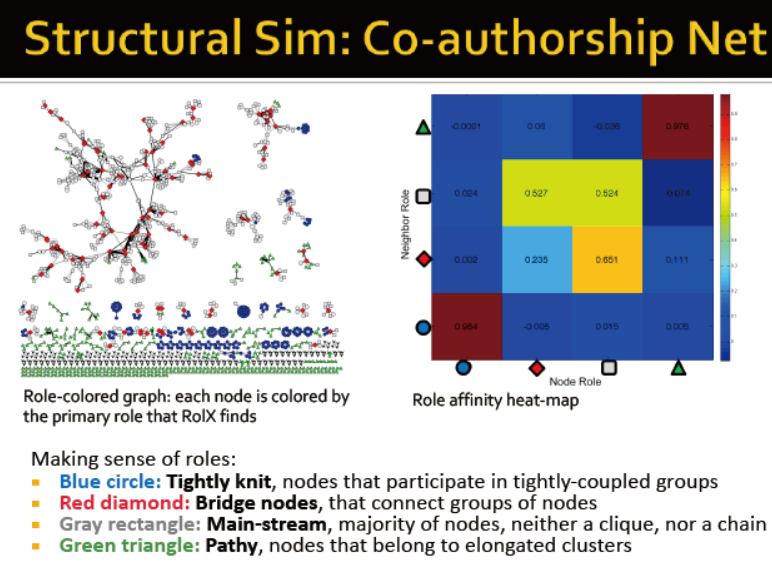
下图是co-authorship的例子
蓝色：连接紧密
红色：桥梁节点，连接两个group
灰色：大部分节点，不属于团，也不属于链
绿色：细长的聚类
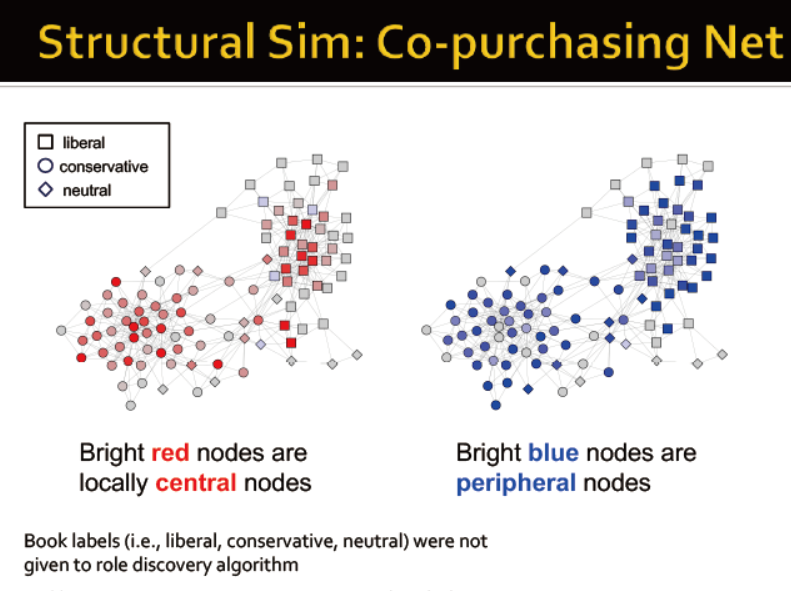
购买网络：红色节点——中心，蓝色——外围
