注:本文翻译自http://www.geeksforgeeks.org/articulation-points-or-cut-vertices-in-a-graph/。如有翻译错误请指正。
一个无向联通图(undirected connected graph)中的顶点,当且仅当去掉它会使图不再联通,就是割点(articulation point/cut vertex)。割点表示一个连通网络的脆弱性——一个点出问题会将整个网络分成2个或更多个部分。在设计可靠的网络中,它们很有用。
对于一个无向联通图,一个割点是一个去掉之后会增加连通分量(connected component)数量的点。
下面是一些例子,割点用红色圆圈圈出:

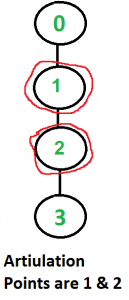
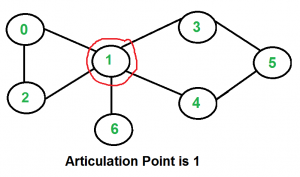
怎么找到一个图里的全部割点?
一个简单方法就是一个接一个地去掉所有顶点,然后看去掉该点是否导致图不再连通。下面是这种简单方法的步骤:
对于每个顶点v
a) 将v从图中去掉
b) 看图是否仍是连通的(既可以使用BFS,也可以使用DFS)
c) 将v重新加入图
上述方法的时间复杂度为O(V*(V+E)),如果使用邻接表存储图。可以更好吗?
寻找所有割点的O(V+E)算法
方法是使用DFS(depth first search,深度优先搜索)。在DFS中,我们用树的形式跟踪顶点,叫做DFS树。在DFS树中,一个顶点u是另一个顶点v的父节点(parent),如果v已经被u发现(很明显v在图上与u相邻)。在DFS树中,如果以下两个条件之一成立,则u是割点:
1) u是DFS树的根节点,并且有两个以上的子节点。
2) u不是DFS树的根节点,它有一个子节点v,并且以v为根节点的子树中,没有一个顶点有通向任意一个u的祖先的回边。
下面的图片显示了与上面一样的概念,还有一点补充,就是DFS树中的叶节点不可能是割点。

对于给定的图,我们用DFS遍历和附加代码,寻找割点(articulation points,APs)。在DFS遍历中,我们维护一个parent[]数组,parent[u]存储u的父节点。在上面提及的两种情况中,第一种情况很好检测。对于每个顶点,数出其子节点数量。如果目前访问过的顶点u是根节点(parent[u]为NIL),并且有两个以上的子节点,输出。
第二种情况怎么处理?第二种情况更复杂。我们维护一个disc[]数组,存储一个顶点被发现的时刻(译者注:即从根节点开始,该点是第几个被访问的)。对于每个节点u,我们需要找到最早访问过的顶点(访问时刻最低的顶点),且该顶点可以从以u为根节点的子树(的某个顶点)到达。因此我们维护一个额外的数组low[],定义如下。
low[u] = min(disc[u], disc[w])
w为u的祖先,并且存在一条回边,可以从u的后代到达w。
下面是用来寻找割点的Tarjan算法的C++、Java和Python实现。
C++
// A C++ program to find articulation points in an undirected graph #include<iostream> #include <list> #define NIL -1 using namespace std; // A class that represents an undirected graph class Graph { int V; // No. of vertices list<int> *adj; // A dynamic array of adjacency lists void APUtil(int v, bool visited[], int disc[], int low[], int parent[], bool ap[]); public: Graph(int V); // Constructor void addEdge(int v, int w); // function to add an edge to graph void AP(); // prints articulation points }; Graph::Graph(int V) { this->V = V; adj = new list<int>[V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); adj[w].push_back(v); // Note: the graph is undirected } // A recursive function that find articulation points using DFS traversal // u --> The vertex to be visited next // visited[] --> keeps tract of visited vertices // disc[] --> Stores discovery times of visited vertices // parent[] --> Stores parent vertices in DFS tree // ap[] --> Store articulation points void Graph::APUtil(int u, bool visited[], int disc[], int low[], int parent[], bool ap[]) { // A static variable is used for simplicity, we can avoid use of static // variable by passing a pointer. static int time = 0; // Count of children in DFS Tree int children = 0; // Mark the current node as visited visited[u] = true; // Initialize discovery time and low value disc[u] = low[u] = ++time; // Go through all vertices aadjacent to this list<int>::iterator i; for (i = adj[u].begin(); i != adj[u].end(); ++i) { int v = *i; // v is current adjacent of u // If v is not visited yet, then make it a child of u // in DFS tree and recur for it if (!visited[v]) { children++; parent[v] = u; APUtil(v, visited, disc, low, parent, ap); // Check if the subtree rooted with v has a connection to // one of the ancestors of u low[u] = min(low[u], low[v]); // u is an articulation point in following cases // (1) u is root of DFS tree and has two or more chilren. if (parent[u] == NIL && children > 1) ap[u] = true; // (2) If u is not root and low value of one of its child is more // than discovery value of u. if (parent[u] != NIL && low[v] >= disc[u]) ap[u] = true; } // Update low value of u for parent function calls. else if (v != parent[u]) low[u] = min(low[u], disc[v]); } } // The function to do DFS traversal. It uses recursive function APUtil() void Graph::AP() { // Mark all the vertices as not visited bool *visited = new bool[V]; int *disc = new int[V]; int *low = new int[V]; int *parent = new int[V]; bool *ap = new bool[V]; // To store articulation points // Initialize parent and visited, and ap(articulation point) arrays for (int i = 0; i < V; i++) { parent[i] = NIL; visited[i] = false; ap[i] = false; } // Call the recursive helper function to find articulation points // in DFS tree rooted with vertex 'i' for (int i = 0; i < V; i++) if (visited[i] == false) APUtil(i, visited, disc, low, parent, ap); // Now ap[] contains articulation points, print them for (int i = 0; i < V; i++) if (ap[i] == true) cout << i << " "; } // Driver program to test above function int main() { // Create graphs given in above diagrams cout << " Articulation points in first graph "; Graph g1(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); g1.AP(); cout << " Articulation points in second graph "; Graph g2(4); g2.addEdge(0, 1); g2.addEdge(1, 2); g2.addEdge(2, 3); g2.AP(); cout << " Articulation points in third graph "; Graph g3(7); g3.addEdge(0, 1); g3.addEdge(1, 2); g3.addEdge(2, 0); g3.addEdge(1, 3); g3.addEdge(1, 4); g3.addEdge(1, 6); g3.addEdge(3, 5); g3.addEdge(4, 5); g3.AP(); return 0; }
Java
// A Java program to find articulation points in an undirected graph import java.io.*; import java.util.*; import java.util.LinkedList; // This class represents an undirected graph using adjacency list // representation class Graph { private int V; // No. of vertices // Array of lists for Adjacency List Representation private LinkedList<Integer> adj[]; int time = 0; static final int NIL = -1; // Constructor Graph(int v) { V = v; adj = new LinkedList[v]; for (int i=0; i<v; ++i) adj[i] = new LinkedList(); } //Function to add an edge into the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v's list. adj[w].add(v); //Add v to w's list } // A recursive function that find articulation points using DFS // u --> The vertex to be visited next // visited[] --> keeps tract of visited vertices // disc[] --> Stores discovery times of visited vertices // parent[] --> Stores parent vertices in DFS tree // ap[] --> Store articulation points void APUtil(int u, boolean visited[], int disc[], int low[], int parent[], boolean ap[]) { // Count of children in DFS Tree int children = 0; // Mark the current node as visited visited[u] = true; // Initialize discovery time and low value disc[u] = low[u] = ++time; // Go through all vertices aadjacent to this Iterator<Integer> i = adj[u].iterator(); while (i.hasNext()) { int v = i.next(); // v is current adjacent of u // If v is not visited yet, then make it a child of u // in DFS tree and recur for it if (!visited[v]) { children++; parent[v] = u; APUtil(v, visited, disc, low, parent, ap); // Check if the subtree rooted with v has a connection to // one of the ancestors of u low[u] = Math.min(low[u], low[v]); // u is an articulation point in following cases // (1) u is root of DFS tree and has two or more chilren. if (parent[u] == NIL && children > 1) ap[u] = true; // (2) If u is not root and low value of one of its child // is more than discovery value of u. if (parent[u] != NIL && low[v] >= disc[u]) ap[u] = true; } // Update low value of u for parent function calls. else if (v != parent[u]) low[u] = Math.min(low[u], disc[v]); } } // The function to do DFS traversal. It uses recursive function APUtil() void AP() { // Mark all the vertices as not visited boolean visited[] = new boolean[V]; int disc[] = new int[V]; int low[] = new int[V]; int parent[] = new int[V]; boolean ap[] = new boolean[V]; // To store articulation points // Initialize parent and visited, and ap(articulation point) // arrays for (int i = 0; i < V; i++) { parent[i] = NIL; visited[i] = false; ap[i] = false; } // Call the recursive helper function to find articulation // points in DFS tree rooted with vertex 'i' for (int i = 0; i < V; i++) if (visited[i] == false) APUtil(i, visited, disc, low, parent, ap); // Now ap[] contains articulation points, print them for (int i = 0; i < V; i++) if (ap[i] == true) System.out.print(i+" "); } // Driver method public static void main(String args[]) { // Create graphs given in above diagrams System.out.println("Articulation points in first graph "); Graph g1 = new Graph(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); g1.AP(); System.out.println(); System.out.println("Articulation points in Second graph"); Graph g2 = new Graph(4); g2.addEdge(0, 1); g2.addEdge(1, 2); g2.addEdge(2, 3); g2.AP(); System.out.println(); System.out.println("Articulation points in Third graph "); Graph g3 = new Graph(7); g3.addEdge(0, 1); g3.addEdge(1, 2); g3.addEdge(2, 0); g3.addEdge(1, 3); g3.addEdge(1, 4); g3.addEdge(1, 6); g3.addEdge(3, 5); g3.addEdge(4, 5); g3.AP(); } } // This code is contributed by Aakash Hasija
Python
# Python program to find articulation points in an undirected graph from collections import defaultdict #This class represents an undirected graph #using adjacency list representation class Graph: def __init__(self,vertices): self.V= vertices #No. of vertices self.graph = defaultdict(list) # default dictionary to store graph self.Time = 0 # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) self.graph[v].append(u) '''A recursive function that find articulation points using DFS traversal u --> The vertex to be visited next visited[] --> keeps tract of visited vertices disc[] --> Stores discovery times of visited vertices parent[] --> Stores parent vertices in DFS tree ap[] --> Store articulation points''' def APUtil(self,u, visited, ap, parent, low, disc): #Count of children in current node children =0 # Mark the current node as visited and print it visited[u]= True # Initialize discovery time and low value disc[u] = self.Time low[u] = self.Time self.Time += 1 #Recur for all the vertices adjacent to this vertex for v in self.graph[u]: # If v is not visited yet, then make it a child of u # in DFS tree and recur for it if visited[v] == False : parent[v] = u children += 1 self.APUtil(v, visited, ap, parent, low, disc) # Check if the subtree rooted with v has a connection to # one of the ancestors of u low[u] = min(low[u], low[v]) # u is an articulation point in following cases # (1) u is root of DFS tree and has two or more chilren. if parent[u] == -1 and children > 1: ap[u] = True #(2) If u is not root and low value of one of its child is more # than discovery value of u. if parent[u] != -1 and low[v] >= disc[u]: ap[u] = True # Update low value of u for parent function calls elif v != parent[u]: low[u] = min(low[u], disc[v]) #The function to do DFS traversal. It uses recursive APUtil() def AP(self): # Mark all the vertices as not visited # and Initialize parent and visited, # and ap(articulation point) arrays visited = [False] * (self.V) disc = [float("Inf")] * (self.V) low = [float("Inf")] * (self.V) parent = [-1] * (self.V) ap = [False] * (self.V) #To store articulation points # Call the recursive helper function # to find articulation points # in DFS tree rooted with vertex 'i' for i in range(self.V): if visited[i] == False: self.APUtil(i, visited, ap, parent, low, disc) for index, value in enumerate (ap): if value == True: print index, # Create a graph given in the above diagram g1 = Graph(5) g1.addEdge(1, 0) g1.addEdge(0, 2) g1.addEdge(2, 1) g1.addEdge(0, 3) g1.addEdge(3, 4) print " Articulation points in first graph " g1.AP() g2 = Graph(4) g2.addEdge(0, 1) g2.addEdge(1, 2) g2.addEdge(2, 3) print " Articulation points in second graph " g2.AP() g3 = Graph (7) g3.addEdge(0, 1) g3.addEdge(1, 2) g3.addEdge(2, 0) g3.addEdge(1, 3) g3.addEdge(1, 4) g3.addEdge(1, 6) g3.addEdge(3, 5) g3.addEdge(4, 5) print " Articulation points in third graph " g3.AP() #This code is contributed by Neelam Yadav
输出:
Articulation points in first graph
0 3
Articulation points in second graph
1 2
Articulation points in third graph
1
时间复杂度:上面的函数是一个含有额外数组的简单DFS。因此时间复杂度与DFS相同,对于用邻接表表示的图,为O(V+E)。
引用
https://www.cs.washington.edu/education/courses/421/04su/slides/artic.pdf
http://www.slideshare.net/TraianRebedea/algorithm-design-and-complexity-course-8
http://faculty.simpson.edu/lydia.sinapova/www/cmsc250/LN250_Weiss/L25-Connectivity.htm