Given an array of n integers where n > 1,
nums, return an array output such that output[i] is equal to the product of all the elements of nums except nums[i].Solve it without division and in O(n).
For example, given
[1,2,3,4], return [24,12,8,6].Follow up:
Could you solve it with constant space complexity? (Note: The output array does not count as extra space for the purpose of space complexity analysis.)
Could you solve it with constant space complexity? (Note: The output array does not count as extra space for the purpose of space complexity analysis.)
[Thoughts]
一般这种题都可以分解成若干子问题来解决。As defined,
output[i] is equal to the product of all the elements of nums except nums[i].简单的说
output[i] = { i 前面的数的乘积} X { i 后面的数的乘积}
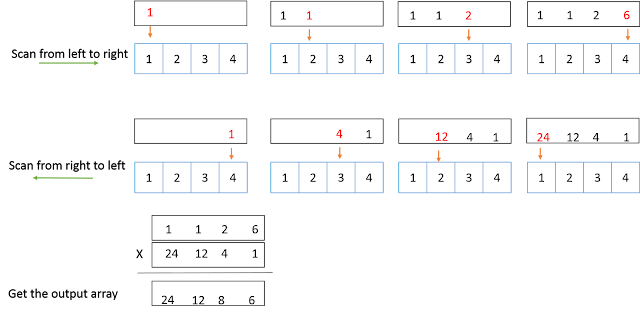
问题就解决了,首先从前往后扫描数组一遍,对每一个i,得到{i 前面的数的乘积}(可以称做output_before),然后在从后往前扫描数组一遍,获得 { i 后面的数的乘积}(可以称做output_after)。 将两数相乘即为所求。
举个例子(如下图),nums = {1,2,3,4}, 第一遍,从前往后扫描一遍,得到的output_before = {1, 1, 2, 6}. 从后往前扫描一遍,得到的output_after = {24, 12, 4, 1}.
那么 output [i] = output_before[i] * output_after[i], output = {24, 12, 8, 6}
[Code]
1: class Solution {
2: public:
3: vector<int> productExceptSelf(vector<int>& nums) {
4: vector<int> products;
5: if(nums.size() == 0) return products;
6: int product = 1;
7: products.push_back(1);
8: for(int i =1; i< nums.size(); i++) {
9: product *= nums[i-1];
10: products.push_back(product);
11: }
12: product = 1;
13: for(int i =nums.size()-2; i>=0; i--) {
14: product = product * nums[i+1];
15: products[i] = products[i] * product;
16: }
17: return products;
18: }
19: };
github: https://github.com/codingtmd/leetcode/blob/master/src/Product%20of%20Array%20Except%20Self.cpp