LeetCode刷题总结之双指针法

Leetcode刷题总结

目前已经刷了50道题，从零开始刷题学到了很多精妙的解法和深刻的思想，因此想按方法对写过的题做一个总结

双指针法

双指针法有时也叫快慢指针，在数组里是用两个整型值代表下标，在链表里是两个指针，一般能实现O（n）的时间解决问题，两个指针的位置一般在第一个元素和第二个元素或者第一个元素和最后一个元素，快指针在前“探路”，当符合某种条件时慢指针向前挪

盛最多水的容器

这道题其实是求最大面积，最大面积取决于较小值。初始时两指针分别位于第一和最后一个元素处，那么明确指针应该向什么方向移动是解题的关键。既然最大面积取决于较小值，那么指针应向较大值方向移动：当指针移动的时候，底在减小，那么假如向较小值方向移，那么由于底变小，高小于等于前一次的高，此时面积肯定小于之前的面积，每一次移动更新一次面积值。

时间：O（n）

空间：O（1）

代码如下：

int maxArea(vector<int>& height) {
         int i=0,j=height.size()-1;
          int maxA=0;
         while(j-i>=1)
          {
              maxA=max(maxA,(min(height[i],height[j]))*(j-i));
              if(height[i]<=height[j])
                  i++;
              else
                  j--;
         }
         return maxA;
 }

View Code

　2. 三数之和

此题的子步骤是两数之和，固定一个数，寻找target=-nums[i]的两个数，采用二分查找的方法（O（logn）），二分法的基础是有序，因此需要先对其进行排序操作

时间：O（nlogn）+O（nlogn）

空间：O（1）结果数组不算

代码如下：

vector<vector<int>> threeSum(vector<int>& nums) {
        int n=nums.size();
        sort(nums.begin(),nums.end());
        if(n<3||nums[0]>0||nums[n-1]<0)
            return {};
        vector<vector<int>> res;
    for(int i=0;i<n-2;i++)
    {
        if(nums[i]>0)
            break;
        if(i>0&&nums[i]==nums[i-1])
            continue;
        int l=i+1,r=n-1;
        while(l<r)
        {
            if(nums[l]+nums[r]==-nums[i])
            {
                vector<int> t;
                t.push_back(nums[i]);
                t.push_back(nums[l]);
                t.push_back(nums[r]);
                res.push_back(t);
                l++;
                r--;
                while(l<r&&nums[l]==nums[l-1])
                    l++;
                while(l<r&&nums[r]==nums[r+1])
                    r--;    
            }
            else if(nums[l]+nums[r]<-nums[i])
                l++;
            else
                r--;
        } 
    }
    return res;
    }

View Code

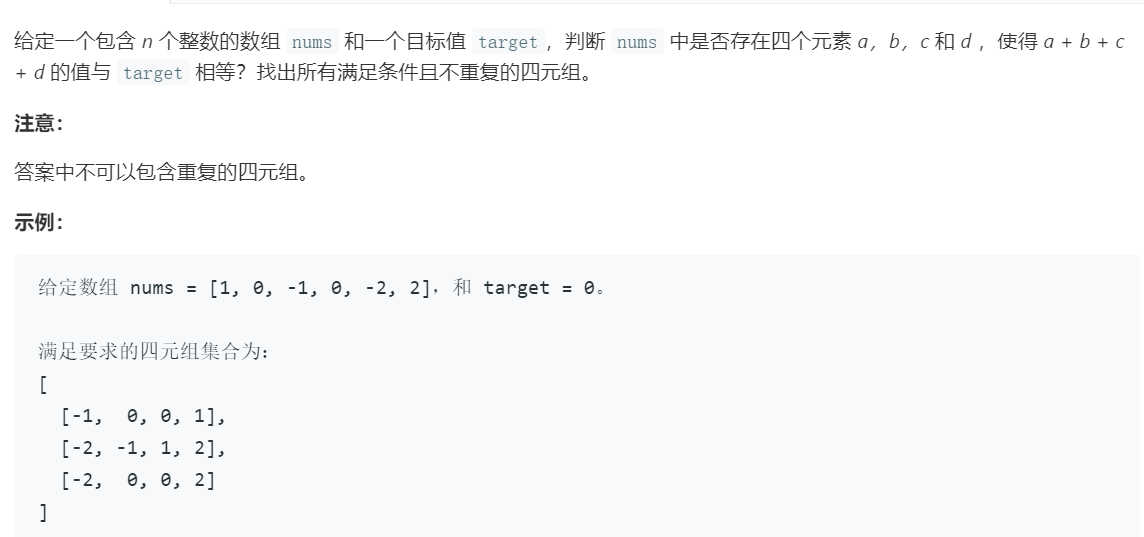
　　3. 四数之和

、

此题的子步骤是三数之和，三数之和的子步骤是两数之和，因此要定两个数，寻找剩下的两个

代码如下：

vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> res;
        set<vector<int>> a;
        int n=nums.size();
        sort(nums.begin(),nums.end());
        if(n<4)
            return {};
        for(int i=0;i<n-3;i++)
        {
            for(int j=i+1;j<n;j++)
            {
                int l=j+1,r=n-1;
                while(l<r)
                {
                    if(nums[i]+nums[j]+nums[l]+nums[r]==target)
                    {
                        a.insert(vector<int>{nums[i],nums[j],nums[l],nums[r],});
                        l++;
                        r--;
                    }
                    else if(nums[i]+nums[j]+nums[l]+nums[r]>target)
                        r--;
                    else
                        l++;
                }
            }
        }
        for(auto c:a)
        {
            res.push_back(c);
        }
        return res;
    }

View Code

　　4. 最接近三数之和

int threeSumClosest(vector<int>& nums, int target) {
        int n=nums.size();
        sort(nums.begin(),nums.end());
            int res;
            int min=INT_MAX;
            for(int i=0;i<n-2;i++)
            {
                int l=i+1,r=n-1;
                
                while(l<r)
                {
                    if(abs(target-nums[i]-nums[l]-nums[r])<min)
                    {
                        min=abs(target-nums[i]-nums[l]-nums[r]);
                        res=nums[i]+nums[l]+nums[r];
                    }
                    if(nums[i]+nums[l]+nums[r]>target)
                        r--;
                    else
                        l++;
                }
            }
            return res;
    }

View Code

以上是关于数组的一些典型题目，下面是关于链表的一些比较好的例子　　

　　5. 删除链表的倒数第N个节点

这道题有姊妹题：获取数组的倒数第N个元素，获取链表的倒数第N个元素，这些题当然可以先遍历一遍获得长度，然后再遍历一遍，但是此时时间是O（2n），而双指针法则可以到达O（n）

初始时将慢指针置于head，快指针置于第n+1个元素处，然后快慢指针通过循环同时向后遍历，直到快指针为NULL，删除慢指针此时指向的节点

为什么是第n+1个呢？因为是要删除倒数第N个元素，需要获得要删除的节点的前一个节点才可以实现删除后仍然连接

时间：O（n）

空间：O（1）

代码如下：

ListNode* removeNthFromEnd(ListNode* head, int n) {
        
        if(n==0)
            return head;
        if(head==NULL)
            return head;
        ListNode* v=head;
        ListNode* u=head;
        for(int i=0;i<n;i++)
            v=v->next;
        if(v==NULL)
        {
            head=head->next;
            return head;
        }
        while(v->next!=NULL)
        {
            u=u->next;
            v=v->next;
        }
            u->next=u->next->next;
        return head;
    }

View Code

　　6. 相交链表

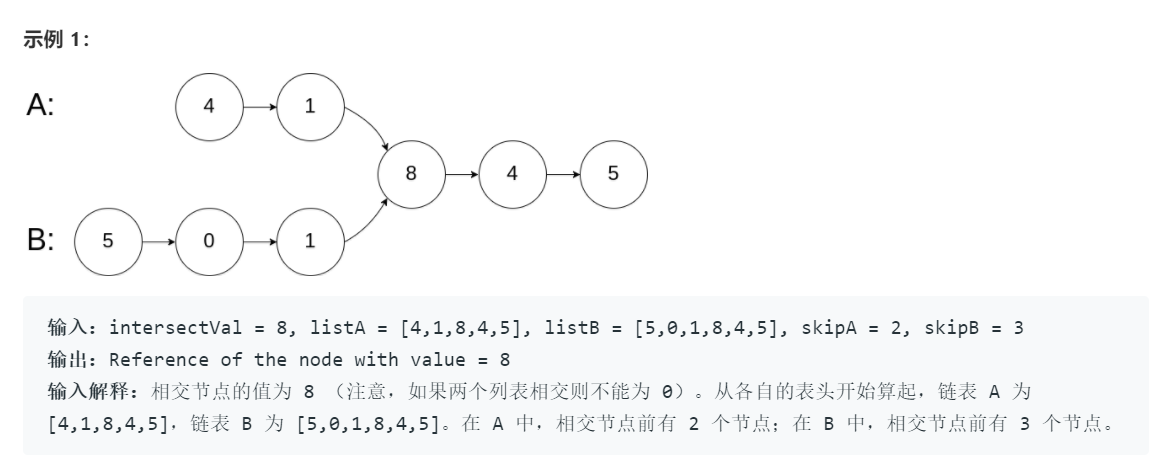
这道题方法有多种，第一种暴力法，第二种利用哈希表，先将A的所有节点插入哈希表种，然后遍历B找到重复的节点，时间是O（m+n），但是空间是O（m）或O（n）

双指针法做法如下：

创建两个指针
当 pApA 到达链表的尾部时，将它重定位到链表 B 的头结点 (你没看错，就是链表 B); 类似的，当 pBpB 到达链表的尾部时，将它重定位到链表 A 的头结点。
若在某一时刻

时间：O（m+n）

空间：O（1）

代码如下：

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(!headA||!headB) return NULL;
        int m=0,n=0;
        ListNode *p=headA;
        ListNode *q=headB;
        while(p){
             m++;
             p=p->next; 
        }
        while(q){
            n++;
            q=q->next;
        }
        p=headA;
        q=headB;
        if(m>n){
             for(int i=0;i<m-n;i++)
                 p=p->next;
        }
        if(m<n){
            for(int i=0;i<n-m;i++)
                 q=q->next;
        }
        while(p&&q&&p!=q){
            p=p->next;
            q=q->next;
        }
        if(!p) return NULL;
        else return p;
    }

View Code

　　7. 环形链表

此题常规方法是哈希表，时间是O（n），空间也是O（n）

双指针法如下：快指针相当于环形跑道上领先的人，慢指针则是落后的人，如果存在环，那么快指针总会追上慢指针而相遇。快指针每次走两步，慢指针每次走一步，快指针相对于慢指针每次走一步。

代码如下：

bool hasCycle(ListNode *head) {
        if(head==NULL||head->next==NULL)
            return 0;
        ListNode* s=head;
        ListNode* f=head->next;
        while(s!=f)
        {
            if(f==NULL||f->next==NULL)
                return 0;
            s=s->next;
            f=f->next->next;
        }
        return 1;
    }

View Code

　　8. 回文链表

此题思想很简单：找到中点，将后半部分翻转，然后与前半部分比较

子步骤是链表的翻转，这个也是leetcode上的一道题（206 翻转链表），快指针每次走两步，慢指针每次走一步，快相对于慢每次走一步，那么当快指针到了尾部的时候，慢指针在中点，然后将以慢指针为头指针的链表进行翻转，再进行比较

时间：O（n）

空间：O（1）

代码如下：

 1 bool isPalindrome(ListNode* head) {
 2         if(head==NULL||head->next==NULL)
 3             return 1;
 4         if(head->next!=NULL&&head->next->next==NULL)
 5         {
 6             if(head->val==head->next->val)
 7                 return 1;
 8             else
 9                 return 0;
10         }
11         ListNode* fast=head;
12         ListNode* slow=head;
13         for(;fast&&fast->next;slow=slow->next,fast=fast->next->next)
14         ;
15         ListNode* back=reverseList(slow);
16         for(ListNode* front=head;front&&back;front=front->next,back=back->next)
17             if(front->val!=back->val)
18                 return 0;
19         return 1;
20 }
21     ListNode* reverseList(ListNode* head)
22     {
23         if(head==NULL||head->next==NULL)
24             return head;
25         ListNode* pre=NULL;
26         ListNode* cur=head;
27         ListNode* next=head;
28         ListNode* res;
29         while(cur!=NULL)
30         {
31             if(next==NULL)
32                 res=cur; 
33             else
34                 next=next->next;
35             cur->next=pre;
36             pre=cur;
37             cur=next;
38         }
39         return res;
40 }

View Code

相关阅读:
抽象工厂模式
 工厂方法模式
 单例模式
 适配器模式
 外观模式
 简单工厂模式
 设计模式开篇闲谈
 android ui更新
 android获取Context
android 事件绑定
原文地址：https://www.cnblogs.com/codingstory/p/11334827.html

热门文章
策略模式
 模板方法模式
 组合模式
 迭代器模式
 命令模式
 观察者模式
 代理模式
 中介者模式
 原型模式
 生成器模式