1.尾调用(Tail Call)
尾调用是函数式编程的一个重要概念,本身非常检点。就是:某个函数的最后一步是调用另一个函数
function f(x){ return g(x); }
函数f的最后一步是调用函数g,这就叫尾调用。
以下情况,都不属于尾调用:
1 // 情况一 2 function f(x) { 3 let y = g(x) 4 return y 5 } 6 7 // 情况二 8 function f(x) { 9 return g(x) + 1 10 } 11 12 // 情况三 13 function f(x) { 14 g(x) 15 }
上面代码中:
- 情况一:调用函数g之后,还有赋值操作,所以不属于尾调用
- 情况二:调用后还有操作
- 情况三等同于:
-
1 function f(x) { 2 if (x > 0) { 3 return m(x) 4 } 5 return n(x); 6 }
-
尾调用不一定出现在函数尾部,只要是最后一步操作即可:
1 function f(x) { 2 if (x > 0) { 3 return m(x) 4 } 5 return n(x); 6 }
上面代码中:函数m和n都属于尾调用,因为它们都是函数f的最后一步操作
2.尾调用优化
尾调用之所以与其他调用不同,就在于它的特殊的调用位置。
(1)正常函数调用:
函数调用会在内存形成一个“调用记录”,又称“调用帧(call frame)”,保存调用位置和内部变量等信息,调用帧可以理解为栈中的一格,如下所示:
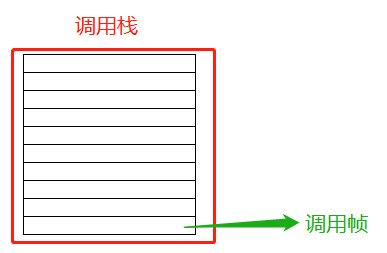
如一个函数:
-
function a(){ b() }
- 上面函数a执行的过程如下:
- 执行到a()时,a被推入调用帧底部
- 执行到a()中的b()方法时,b被压入a上方
- b()执行结束,b()从调用栈中移除
- a()执行结束,a()从调用栈移除,调用栈清空
- 以此类推,多个执行语句先后入栈出栈
(2)函数尾调用
尾调用由于是函数的最后一步操作,所以不需要保留外层函数的调用帧,因为调用位置、内部变量等信息都不会再用到了,只要直接用内层函数的调用帧,取代外层函数的调用帧就可以了。
1 function f(){ 2 let n = 1 3 let m = 2 4 return g(n + m) 5 } 6 f() 7 8 // 等同于 9 function f(){ 10 return g(3) 11 } 12 f() 13 14 // 等同于 15 g(3)
上面代码,如果函数g不是尾调用,函数f就需要保存内部变量m和n的值,g的调用位置等信息。但是由于调用g之后,函数f就结束了,所以执行到最后一步,完全可以删除f(x)的调用帧,只保留g(3)的调用帧。这就叫尾调用优化(Tail call optimization),即只保留内层函数的调用帧,如果所有函数都是尾调用,那么完全可以做到每次执行时,调用帧只有一项,这将大大节省内存。这就是“尾调用优化“的意义。
注意:只有不再用到外层函数的内部变量,内层函数的调用帧才会取代外层函数的调用帧,否则无法进行”尾调用优化“
1 function addOne(a){ 2 var one = 1; 3 function inner(b){ 4 return b + one; 5 } 6 return inner(a); 7 }
因为内层函数inner用到了外层函数addOne的内部变量one。
注意:
- 目前自会有Safari浏览器支持尾调用优化,Chrome和Fiefox都不支持
- ES6的尾调用优化只在严格模式下开启,正常模式下是无效的(因为在正常模式下,函数内部有两个变量,可以跟踪函数的调用栈)
- func.arguments:返回调用时函数的参数
- func.caller:返回调用当前函数的那个函数
- 尾调用优化发生时,函数的调用栈会改写,因此上面两个变量就会失真。严格模式下禁用了这两个变量,所以尾调用优化仅在严格模式下生效
3.尾递归
函数调用自身,称为递归,如果尾调用自身,就称为尾递归
递归非常耗费内存,因为需要同时保存成千上百个调用帧,很容易法伤”栈溢出“(stack overflow)。但是对于尾递归来说,由于只存在一个调用帧,所以永远不会发生栈溢出错误。
(1)示例:计算阶乘
非尾调用:
1 function factorial(n) { 2 if (n === 1) return 1; 3 return n * factorial(n -1) 4 } 5 factorial(5)
上面代码,计算n的阶乘,最多需要保存n个调用记录,复杂度O(n)
尾调用:
1 function factorial(n,total) { 2 if (n === 1) return total; 3 return factorial(n - 1, n * total) 4 } 5 6 factorial(5,1) // 120
改成尾递归,只保留一个调用记录,复杂度O(1)
(2)示例:计算斐波那契数列
1 function Fibonacci (n) { 2 if ( n <= 1 ) {return 1}; 3 4 return Fibonacci(n - 1) + Fibonacci(n - 2); 5 } 6 7 Fibonacci(10) // 89 8 Fibonacci(100) // 超时 9 Fibonacci(500) // 超时
尾递归优化:
1 function Fibonacci2 (n , ac1 = 1 , ac2 = 1) { 2 if( n <= 1 ) {return ac2}; 3 4 return Fibonacci2 (n - 1, ac2, ac1 + ac2); 5 } 6 7 Fibonacci2(100) // 573147844013817200000 8 Fibonacci2(1000) // 7.0330367711422765e+208 9 Fibonacci2(10000) // Infinity
由此可见,”尾调用优化“对递归操作意义重大,所以一些函数式编程语言将其写入了语言规格。ES6也是如此,第一次明确规定,所有ECMAScript的实现,都必须部署"尾调用优化"。这就是说,ES6中只要使用尾递归,就不会发生栈溢出(或者层层递归造成的超时),相对节省内存。
(3)递归函数的改写
尾递归的实现,往往需要改写递归函数,确保最后一步只调用自身。如何做到这一点:
①把所有用到的内部变量改写成函数的参数(缺点:不太直观)
如上面的阶乘函数factorial需要用到一个中间变量total,那就把这个中间比那辆改写成函数的参数。
有两种方法可以解决这个问题:
方法一:再尾递归函数之外,再提供一个正常形式的函数
1 function tailFactorial(n, total) { 2 if (n === 1) return total; 3 return tailFactorial(n - 1, n * total); 4 } 5 6 function factorial(n) { 7 return tailFactorial(n, 1); 8 } 9 10 factorial(5) // 120
上面代码通过一个正常形式的阶乘函数,调用尾递归函数。看起来会正常一点。
函数柯里化:是函数式编程中的一个概念,意思是将多参数的函数转换成单参数的形式。这里也可以使用柯里化:
1 function currying(fn,n){ 2 return function(m){ 3 return fn.call(this,m,n) 4 } 5 } 6 7 function tailFactorial(n,total){ 8 if(n === 1) return total 9 return tailFactorial(n -1, n * total) 10 } 11 12 const factorial = currying(tailFactorial, 1) 13 14 factorial(5)
方法二:ES6的函数默认值
这种方法比较简单。
1 function factorial(n, total = 1) { 2 if (n === 1) return total; 3 return factorial(n - 1, n * total); 4 } 5 6 factorial(5) // 120
参数total有默认值1,所以调用时不用提供这个值
总结一下:递归本质上是一种循环操作。纯粹的函数式编程语言没有循环操作命令,所有的循环都用递归实现,这就是为什么尾递归对这些语言极其重要。对于其他支持“尾调用优化”的语言(比如 Lua,ES6),只需要知道循环可以用递归代替,而一旦使用递归,就最好使用尾递归。
(4)尾递归优化的实现
尾递归优化只在严格模式下生效,正常情况下,或者那些不支持该功能的环境中,可以自己实现尾递归优化。
原理:
尾递归之所以需要优化,原因是调用栈太多,造成溢出,那么只要减少调用栈,就不会溢出。如何实现减少调用栈?就是:使用“循环”换掉“递归”
一个正常的递归函数:
1 function sum(x, y) { 2 if (y > 0) { 3 return sum(x + 1, y - 1); 4 } else { 5 return x; 6 } 7 } 8 9 sum(1, 100000) 10 // Uncaught RangeError: Maximum call stack size exceeded(…)
上面代码中,sum是一个递归函数,参数x是需要累加的值,参数y控制递归次数。一旦指定sum递归 100000 次,就会报错,提示超出调用栈的最大次数。
蹦床函数(trampoline)可以将递归执行转为循环执行。
1 function trampoline(f) { 2 while (f && f instanceof Function) { 3 f = f(); 4 } 5 return f; 6 }
上面就是蹦床函数的一个实现,它接受一个函数f作为参数。只要f执行后返回一个函数,就继续执行。注意,这里是返回一个函数,然后执行该函数,而不是函数里面调用函数,这样就避免了递归执行,从而就消除了调用栈过大的问题。
然后,要做的就是将原来的递归函数,改写为每一步返回另一个函数。
1 function sum(x, y) { 2 if (y > 0) { 3 return sum.bind(null, x + 1, y - 1); 4 } else { 5 return x; 6 } 7 }
上面代码中,sum函数的每次执行,都会返回自身的另一个版本。
现在,使用蹦床函数执行sum,就不会发生调用栈溢出。
trampoline(sum(1, 100000)) // 100001
蹦床函数并不是真正的尾递归优化,下面的实现才是。
1 function tco(f) { 2 var value; 3 var active = false; 4 var accumulated = []; 5 6 return function accumulator() { 7 accumulated.push(arguments); 8 if (!active) { 9 active = true; 10 while (accumulated.length) { 11 value = f.apply(this, accumulated.shift()); 12 } 13 active = false; 14 return value; 15 } 16 }; 17 } 18 19 var sum = tco(function(x, y) { 20 if (y > 0) { 21 return sum(x + 1, y - 1) 22 } 23 else { 24 return x 25 } 26 }); 27 28 sum(1, 100000) 29 // 100001
上面代码中,tco函数是尾递归优化的实现,它的奥妙就在于状态变量active。默认情况下,这个变量是不激活的。一旦进入尾递归优化的过程,这个变量就激活了。然后,每一轮递归sum返回的都是undefined,所以就避免了递归执行;而accumulated数组存放每一轮sum执行的参数,总是有值的,这就保证了accumulator函数内部的while循环总是会执行。这样就很巧妙地将“递归”改成了“循环”,而后一轮的参数会取代前一轮的参数,保证了调用栈只有一层。