什么是跳跃表
Skip list(跳表）是一种可以代替平衡树的数据结构，默认是按照Key值升序的。Skip list让已排序的数据分布在多层链表中，以0-1随机数决定一个数据的向上攀升与否，通过“空间来换取时间”的一个算法，在每个节点中增加了向前的指针，在插入、删除、查找时可以忽略一些不可能涉及到的结点，从而提高了效率。
在Java的API中已经有了实现：分别是
ConcurrentSkipListMap(在功能上对应HashTable、HashMap、TreeMap) ；
ConcurrentSkipListSet(在功能上对应HashSet)
跳跃表以有序的方式在层次化的链表中保存元素， 效率和AVL树媲美 —— 查找、删除、添加等操作都可以在O(LogN)时间下完成（最坏情况下时间复杂性O(n)。相比在一个有序数组或链表中进行插入/删除操作的时间为O(n)，最坏情况下为O(n)）， 并且比起二叉搜索树来说， 跳跃表的实现要简单直观得多。
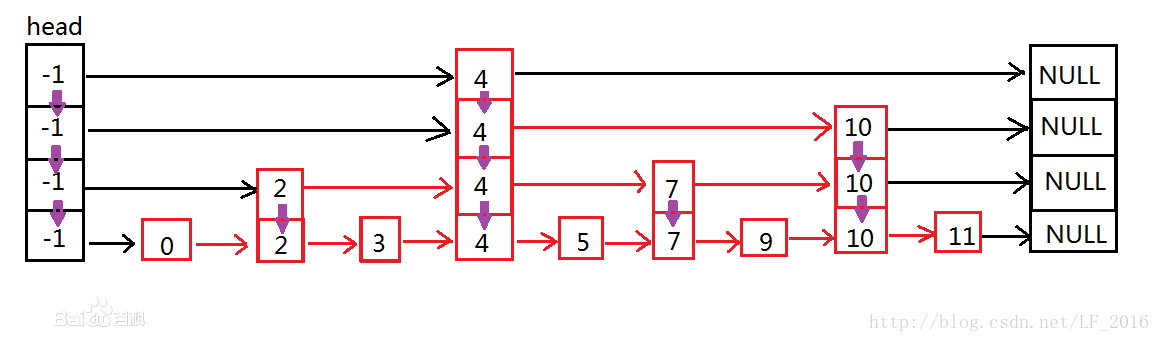
结构图如下：
可以看到跳跃表主要由以下部分构成：
- 表头（head）：负责维护跳跃表的节点指针。
- 跳跃表节点：保存着元素值，以及多个层。
- 层：保存着指向其他元素的指针。高层的指针越过的元素数量大于等于低层的指针，为了提高查找的效率，程序总是从高层先开始访问，然后随着元素值范围的缩小，慢慢降低层次。
- 表尾：全部由 NULL 组成，表示跳跃表的末尾
原理
跳表的原理非常简单，跳表其实就是一种可以进行二分查找的有序链表。跳表的数据结构模型如图1:
可以看到，跳表在原有的有序链表上面增加了多级索引，通过索引来实现快速查找。首先在最高级索引上查找最后一个小于当前查找元素的位置，然后再跳到次高级索引继续查找，直到跳到最底层为止，这时候以及十分接近要查找的元素的位置了(如果查找元素存在的话)。由于根据索引可以一次跳过多个元素，所以跳查找的查找速度也就变快了。
级的分配
在级基本的分配过程中，可以观察到，在一般跳表结构中，i-1级链中的元素属于i级链的概率为p。假设有一随机数产生器值域为[0,RANDMAX]。则下一次所产生的随机数≤CutOff=p*RANDMAX的概率为p。因此，若下一随机数≤CutOff，则新元素应在1级链上。现在继续确定新元素是否在2级链上，这由下一个随机数来决定。若新的随机数≤CutOff，则该元素也属于2级链。重复这个过程，直到得到一随机数＞CutOff为止。故可以用下面的代码为要插入的元素分配级。
intlevel = 0;
while(rand() <= CutOff) level++;
这种方法潜在的缺点是可能为某些元素分配特别大的级，从而导致一些元素的级远远超过log1/pN，其中N为字典中预期的最大数目。为避免这种情况，可以设定一个上限lev。在有N个元素的跳表中，级MaxLevel的最大值为
可以采用此值作为上限。
另一个缺点是即使采用上面所给出的上限，但还可能存在下面的情况，如在插入一个新元素前有三条链，而在插入之后就有了10条链。这时，新插入元素的为9级，尽管在前面插入中没有出现3到8级的元素。也就是说，在此插入前并未插入3，4，⋯，8级元素。既然这些空级没有直接的好处，那么可以把新元素的级调整为3。
构造一个跳跃表
一个跳表，应该具有以下特征：
- 一个跳表应该有几个层（level）组成；
- 跳表的第一层包含所有的元素；
- 每一层都是一个有序的链表；
- 如果元素x出现在第i层，则所有比i小的层都包含x；
- 第i层的元素通过一个down指针指向下一层拥有相同值的元素；
- 在每一层中，-1和1两个元素都出现(分别表示INT_MIN和INT_MAX)；
- Top指针指向最高层的第一个元素。
以下面的链表为例演示如何构造一个跳跃表：
构造一个3层的跳跃表：
Skip List构造步骤：
1、给定一个有序的链表。
2、选择连表中最大和最小的元素，然后从其他元素中按照一定算法（随机）随即选出一些元素，将这些元素组成有序链表。这个新的链表称为一层，原链表称为其下一层。
3、为刚选出的每个元素添加一个指针域，这个指针指向下一层中值同自己相等的元素。Top指针指向该层首元素
4、重复2、3步，直到不再能选择出除最大最小元素以外的元素。
查询
跳跃表只需要从最上层开始遍历，由于每一层的链表都是有序的，因此当查找的“键”不存在于某一层中的时候，只需要在比查找目标的“键”要大的结点向下一次跳跃即可，重复操作，直至跳跃到最底层的链表。
1、先从顶层开始遍历,与16进行对比小，进入下一层。
2、与4进行比较,比4大,当前结点置为4结点，与16进行比较,进入下一层。
3、 与8进行比较,没有比8大,切换为当前结点4。
4、将节点4的下一个节点8和当前值进行比较,相同,取出。
插入
1、函数实现向跳跃表中插入一个“键”为 key，“值”为 value 的结点。由于我们进行插入操作时，插入结点的层数先要确定因此需要进行抛硬币实验确定占有层数。
2、由于新结点根据占有的层数不同，它的后继可能有多个结点，因此需要用一个指针通过“键”进行试探，找到对应的“键”的所有后继结点，在创建结点之后依次修改结点每一层的后继，不要忘了给结点判空。在插入操作时，“键”可能已经存在，此时可以直接覆盖“值”就行了，也可以让用户决定，可以适当发挥。
寻找节点的位置，获取到插入节点的前一个节点,
3、与链表的操作执行相同的节点操作,地址替换。
模拟插入操作
首先我们需要用一个试探指针找到需要插入的结点的前驱，即用红色的框框出来的结点。需要注意的是，由于当前的跳跃表只有 2 层，而新结点被 3 层占有，因此新结点在第 3 层的前驱就是头结点。
接下来的操作与单链表相同，只是需要同时对每一层都操作。如图所示，红色箭头表示结点之间需要切断的逻辑联系，蓝色的箭头表示插入操作新建立的联系。
插入的最终效果应该是如图所示的。
删除
由于需要删除的结点在每一层的前驱的后继都会因删除操作而改变，所以和插入操作相同，需要一个试探指针找到删除结点在每一层的前驱的后继，并拷贝。接着需要修改删除结点在每一层的前驱的后继为删除结点在每一层的后继，保证跳跃表的每一层的逻辑顺序仍然是能够正确描述。
1、根据删除的值找到当前值在跳表中的前驱结点 head 4
2、判断结点4的后驱结点的值是否为8，不是，直接跳出。当前值在跳表中不存在。
3、循环遍历每一层,执行地址变更。当前结点可能在其他层不存在结点，因此在变更的时候要判断是当前层是否存在该结点。
代码
// 跳表中存储的是正整数，并且存储的数据是不重复的
public class SkipListTest {
//最大索引层数
private static int MAX_LEVEL =16;
//头节点
private Node head;
//索引的层级数,默认为1
private int levelCount =1;
private Random random;
class Node{
//结点值
private int value;
//当前节点的所有后驱节点。1-maxlevel 层。
private Node[]nodes =new Node[MAX_LEVEL];
//当前节点的层数
private int maxLevel;
public Node(int value,int maxLevel) {
this.value = value;
this.maxLevel = maxLevel;
}
}
public Node get(int value){
//1、从最高层开始遍历
Node cur =head;
for (int i =levelCount-1; i >=0 ; i--) {
//找到比该值小的那个结点
while (cur.nodes[i]!=null && cur.nodes[i].value < value){
cur = cur.nodes[i];
}
//开始寻找下一层,直到找到最后一层
}
if(cur.nodes[0]!=null&&cur.nodes[0].value == value){
return cur.nodes[0];
}
return null;
}
public void insert(int number){
//1、获取要插入的索引层数量
int level = randomLevel();
//2、创建新节点
Node newNode =new Node(number,level);
//3、获取每一层的前驱结点
Node update[] =new Node[level];
//遍历索引层
Node c =head;
for (int i =level-1; i >=0 ; i--) {
while (c.nodes[i]!=null&&c.nodes[i].value){
c = c.nodes[i];
}
update[i] = c;
}
//4、更新每一层的索引结构
for (int i =0; i // 缺失
//当前结点的后驱结点
newNode.nodes[i] =update[i].nodes[i];
//当前结点的前驱
update[i].nodes[i] =newNode.nodes[i];
}
//5、更新索引层
if(levelCount // 缺失
levelCount =level;
}
}
public void delete(int value){
//1、获取每一层比当前值小的前一个结点
Node[]update =new Node[levelCount];
Node p =head;
for(int i =levelCount -1; i >=0; --i){
while(p.nodes[i] !=null && p.nodes[i].value < value){
p = p.nodes[i];
}
update[i] = p;
}
//2、如果最后一层的结点的与当前值相同,进入变更指针操作。
if(p.nodes[0] !=null && p.nodes[0].value == value){
for(int i =levelCount -1; i >=0; --i){
//从最高层开始变更,如果值相等才进行变更
if(update[i].nodes[i] !=null &&update[i].nodes[i].value == value){
update[i].nodes[i] =update[i].nodes[i].nodes[i];
}
}
}
}
// 随机函数
private int randomLevel(){
int level =1;
for(int i =1; i // 缺失
if(random.nextInt() %2 ==1){
level++;
}
}
return level;
}
}