线性模型是机器学习中应用最广泛的模型,指通过样本特征的线性组合来进行预测的模型。给定一个D维样本 x = [x1,...,xD]T,其线性组合函数为
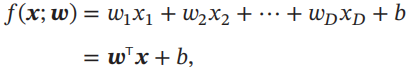
分类问题中,由于输出目标y是一些离散的标签,而f(x;w)的值域为实数,因此无法直接用f(x;w)来进行预测,需要引入一个非线性的决策函数g(.)来预测输出目标
y = g(f(x;w))
二分类问题,g(.)可以是符号函数,定义为
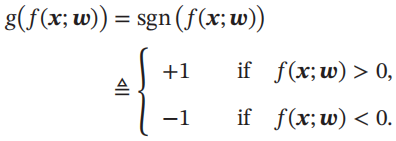
二分类的线性模型如下所示:

3.1 线性判别函数和决策边界
3.1.1 二分类
下图给出了一个二分类问题的线性决策边界示例,其中样本特征向量x = [x1,x2],权重向量w = [w1 , w2]
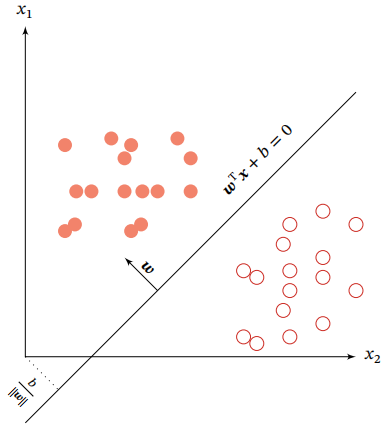
两类线性可分定义:

3.1.2 多分类
多分类问题常用的方式有以下三种:
(1)”一对其余“方式:把多分类问题转换为C个”一对其余“的二分类问题。这种方式共需要C个判别函数,其中第c个判别函数fc是将类别c的样本和不属于c的样本分开。
(2)”一对一“方式:把多分类问题转换为C(C-1)/2个”一对一“的二分类问题。这种方式共需要C(C-1)/2个判别函数,其中第(i,j)个判别函数是把类别i和类别j的样本分开。

下图给出了用这三种方式进行多分类的示例。
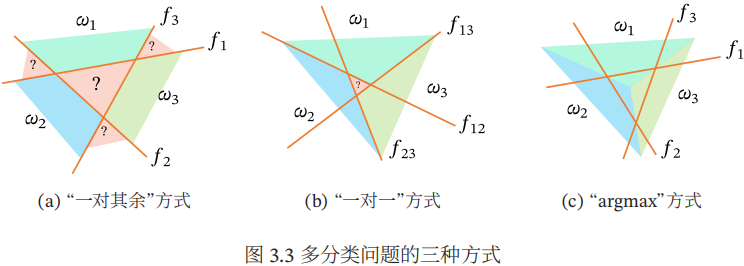
多类线性可分定义:

3.2 Logistic回归
在Logistic回归中,我们使用Logistic函数来作为激活函数。标签y=1的后验概率为
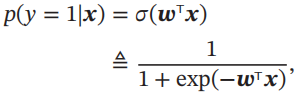
标签y=0的后验概率为
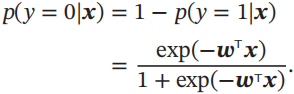
3.2.1 参数学习
Logistic回归采用交叉熵作为损失函数,并使用梯度下降法来对参数进行优化。
使用交叉熵损失函数,其风险函数为
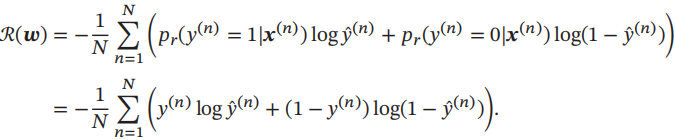
风险函数R(w)关于参数w的偏导数为
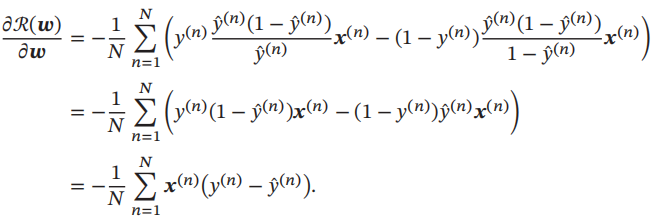
采用梯度下降法,通过下式来迭代更新参数:
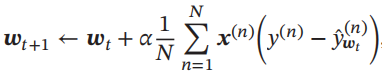
3.3 Softmax回归
给定一个样本x,Softmax回归预测的属于类别c的条件概率为

Softmax回归的决策函数可以表示为
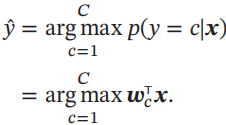
3.3.1 参数学习
采用交叉熵损失函数,Softmax回归模型的风险函数为

风险R(W)关于W的梯度为
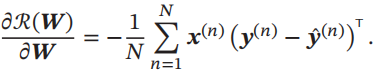
采用梯度下降法,通过下式进行迭代更新:
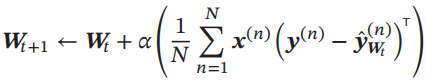
3.4 感知器
感知器可谓是最简单的人工神经网络,只有一个神经元。
3.4.1 参数学习
感知器学习算法试图找到一组参数w*,使得对于每个样本(x(n),y(n))有
y(n) w*T x(n) > 0 , n ∈ {1 , ... , N}
具体的感知器参数学习策略如下所示

感知器的损失函数为L(w;x,y) = max(0,-ywTx)
采用梯度下降,每次更新的梯度为
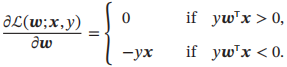
3.4.2 感知器的收敛性

虽然感知器在线性可分的数据上可以保证收敛,但其存在以下不足:
(1)在数据集线性可分时,感知器虽然可以找到一个超平面把两类数据分开,但并不能保证其泛化能力。
(2)感知器对样本顺序比较敏感。每次迭代的顺序不一致时,找到的分割超平面也往往不一致。
(3)如果训练集不是线性可分的,就永远不会收敛。
3.4.3 参数平均感知器
感知器学习到的权重向量和训练样本的顺序相关。在迭代次序上排在后面的错误样本比前面的错误样本,对最终的权重向量影响更大。
为了提高感知器的鲁棒性和泛化能力,我们可以将在感知器学习过程中的所有K个权重向量保存起来,并赋予每个权重向量wk一个置信系数ck(1 <= k <= K)。最终的分类结果通过这K个不同权重的感知器投票决定,这个模型也称为投票感知器。
令τk为第k次更新权重wk时的迭代次数,τk+1为下次权重更新时的迭代次数,则权重wk的置信系数ck设置为从τk到τk+1之间间隔的迭代次数,即ck = τk+1 - τk.置信系数ck越大,说明权重wk在之后的训练过程中正确分类样本的数量越多,越值得信赖。
这样,投票感知器的形式为

3.5 支持向量机
支持向量机是一个经典的二分类算法,其找到的分割超平面具有更好的鲁棒性。
给定一个二分类数据集D = { ( x(n) , y(n) ) },其中 yn ∈ { +1 , -1},如果两类样本是线性可分的,即存在一个超平面 wTx + b = 0
将两类样本分开,那么对于每个样本都有 y(n) ( wT x(n) + b) > 0
数据集D中每个样本x(n)到分割超平面的距离为:
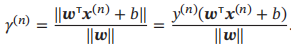
定义间隔γ为整个数据集D中所有样本到分割超平面的最短距离: γ = min γ(n)
间隔γ越大,其分割超平面对两个数据集的划分越稳定,不容易受噪声等因素影响。支持向量机的目标是寻找一个超平面(w* , b*)使得γ最大,即
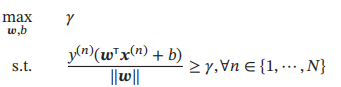
令||w|| * γ = 1,则上式等价于
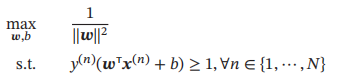
数据集中所有满足y(n)(wTx(n) + b) = 1的样本点,都称为支持向量
3.5.1 参数学习
为了找到最大间隔分割超平面,将上式的目标函数写为凸优化问题
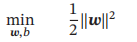

使用拉格朗日乘数法
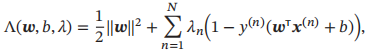
令其关于w和b的导数求导之后等于0,得到
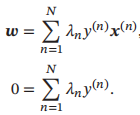
代入拉格朗日函数,得到拉格朗日对偶函数

最优参数的支持向量机的决策函数为
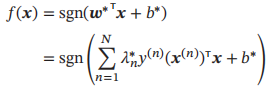
3.5.2 核函数
支持向量机可以使用核函数隐式地将样本从原始特征空间映射到更高维的空间,并解决原始特征空间中的线性不可分问题。在一个变换后的特征空间φ中,支持向量机的决策函数为
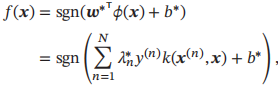
3.5.3 软间隔
如果训练集中的样本在特征空间中不是线性可分的,就无法找到最优解。为了能够容忍部分不满足约束的样本,可以引入松弛变量ξ,将优化问题变为
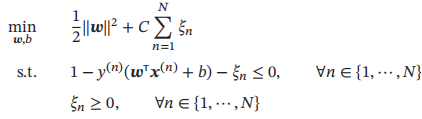
3.6 损失函数对比
Logistic回归的损失函数可以改写为
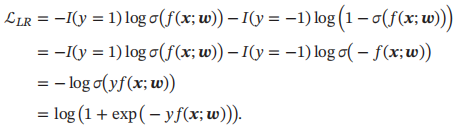
感知器的损失函数为
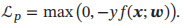
软间隔支持向量机的损失函数为
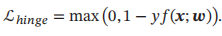
平方损失可以重写为
