一、回顾
在上一篇博客中,我们已经分析出了插入一个节点之后,红黑树需要如何进行调整对应的三种情形:
首先:新插入红黑树的节点一定是红色
- 若新插入节点的爸爸是黑色节点,红黑树不需要调整
- 若新插入节点的爸爸和它叔叔都是红色节点,红黑树只需要变色,不需要旋转
- 若新插入节点的爸爸是红色,但是它叔叔是黑色(可能为null,但是null是叶子节点,正儿八经的黑色),这时,一定是变色+旋转。
对于情形一二,我们给出了例子,也通过看源码得到了验证,现在我们就先来举一个例子,满足第三种情形:
首先看这样一个红黑树:
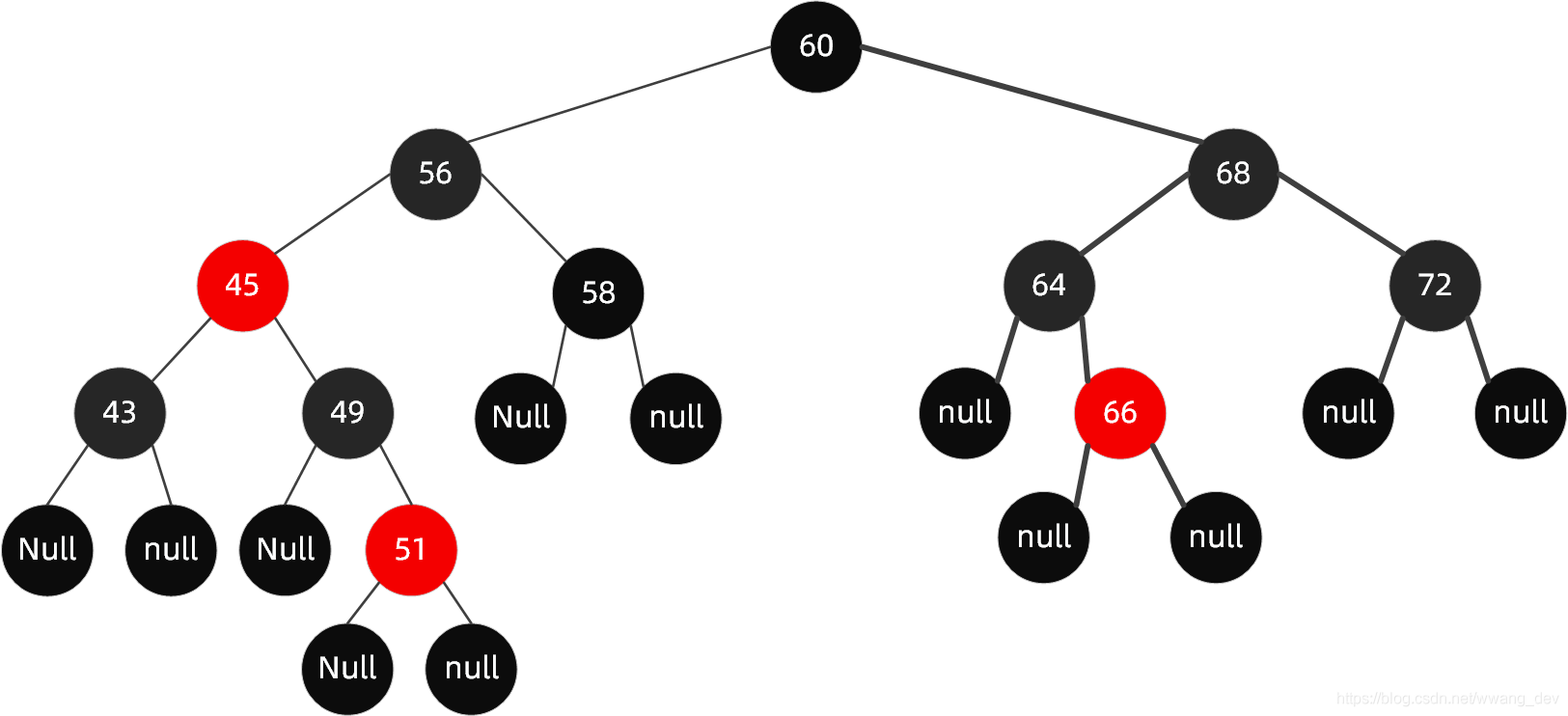
我们向其中插入【65】,它应该会成为【66】的左孩子
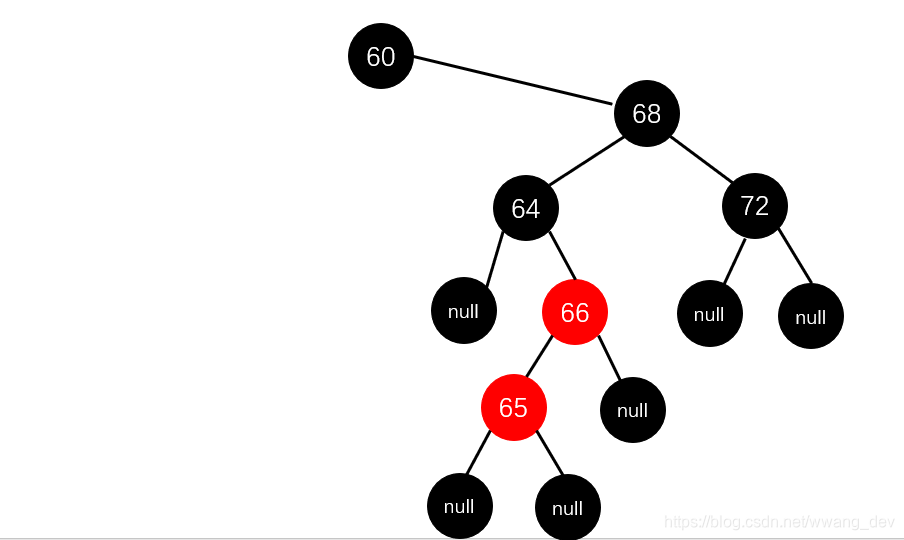
我们发现破坏了两个规则:1. 【66】和【65】都是红色 。2.【64】的右子树高度比左子树高2,也就是从根到叶子节点的路径上的黑色节点数不一样
首先,我们通过变色解决1
把【65】的爸爸【64】变成黑色;把【64】的爷爷变成【红色】
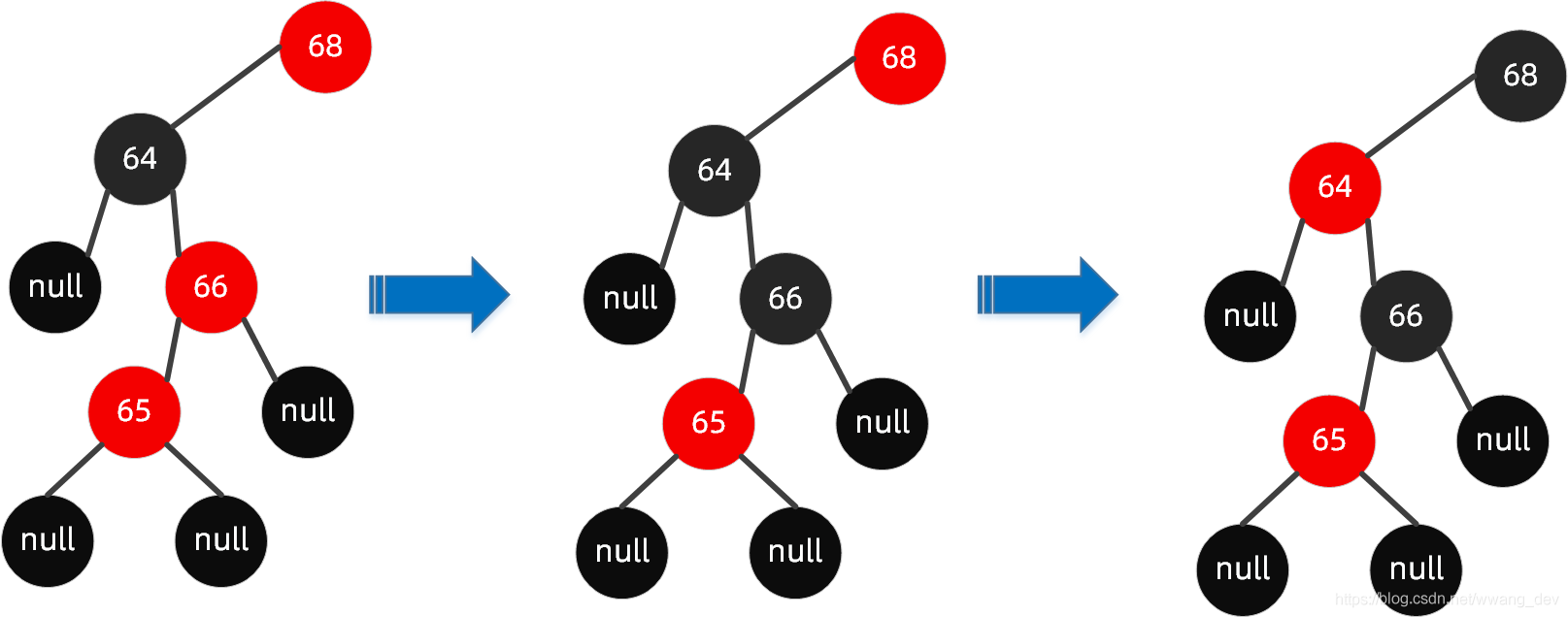
然后,无论怎么变色,都不会改变树的高度,所以我们必须借助旋转。
二、旋转操作的四种情形
1. 左左插入后旋转
这种情况下,父节点和插入的节点都是左节点,
这种情况下,我们要插入节点【65】
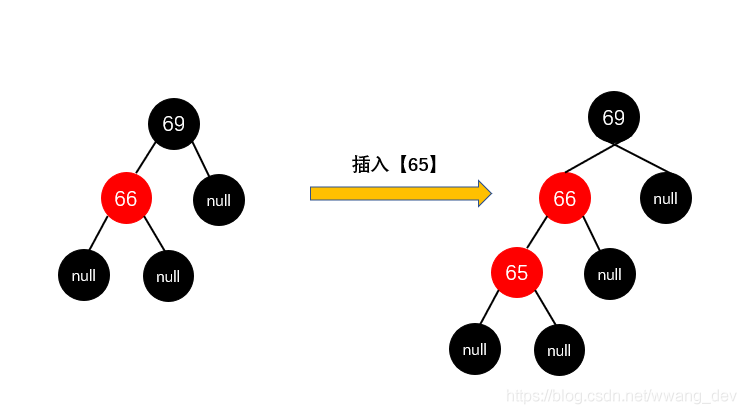
规则如下:先【变色】解决连续红色问题,再【旋转】解决高度差问题
- 把它爸爸【66】变成黑色,把它爷爷【69】变成红色
- 它爷爷【69】右旋
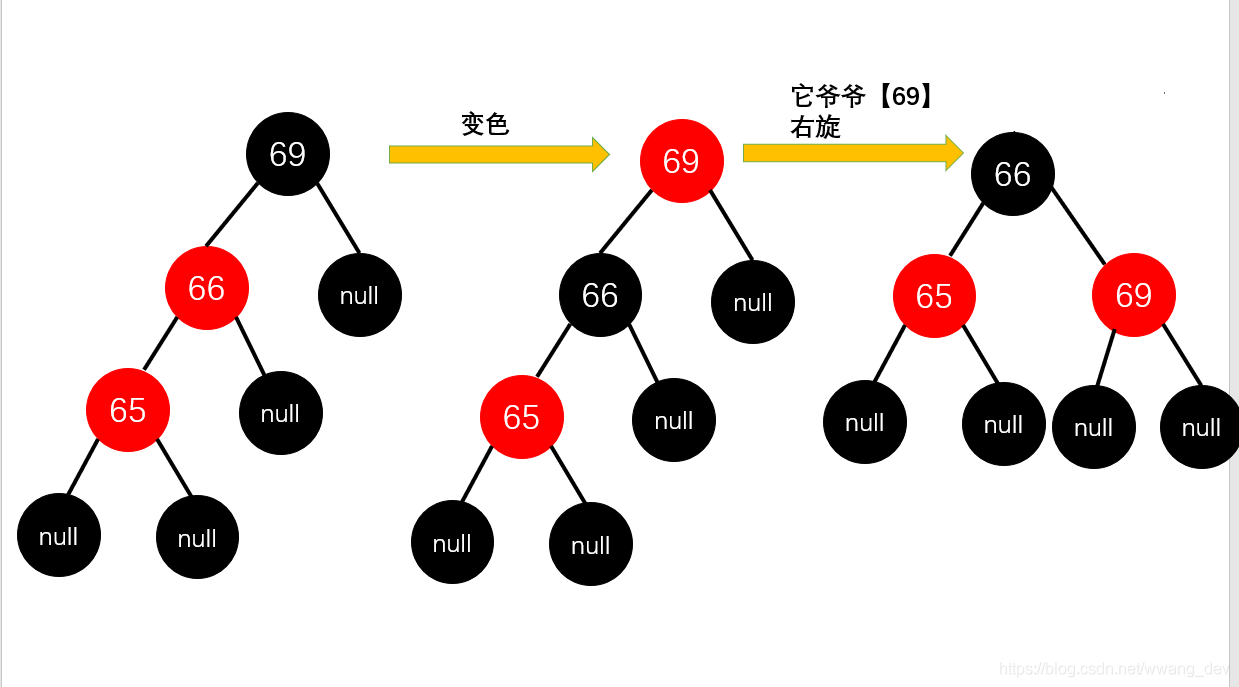
2. 左右插入后旋转
这种情况下,父节点是左节点,插入的节点是右节点,
这种情况下,我们要插入节点【67】
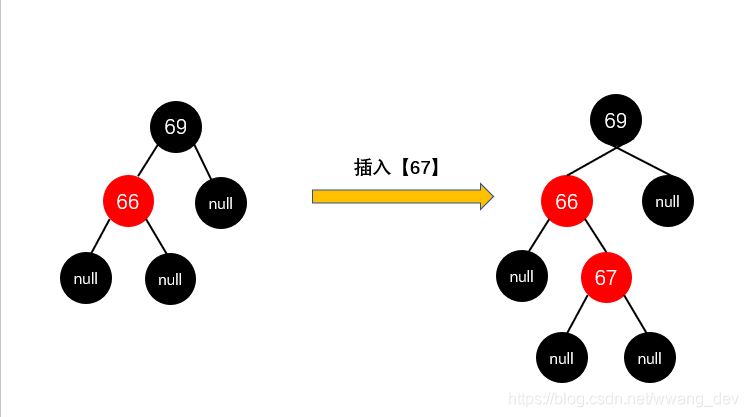
规则如下:先旋转使得偏向一边,再【变色】解决连续红色问题,再【旋转】解决高度差问题:
- 它爸爸【66】左旋,偏向左边,左旋之后【66】变成了儿子,【67】变成了爸爸,(相当于是【66】成了新插入的红色节点)
- 把它爸爸【67】变成黑色,把它爷爷【69】变成红色
- 它爷爷【69】右旋
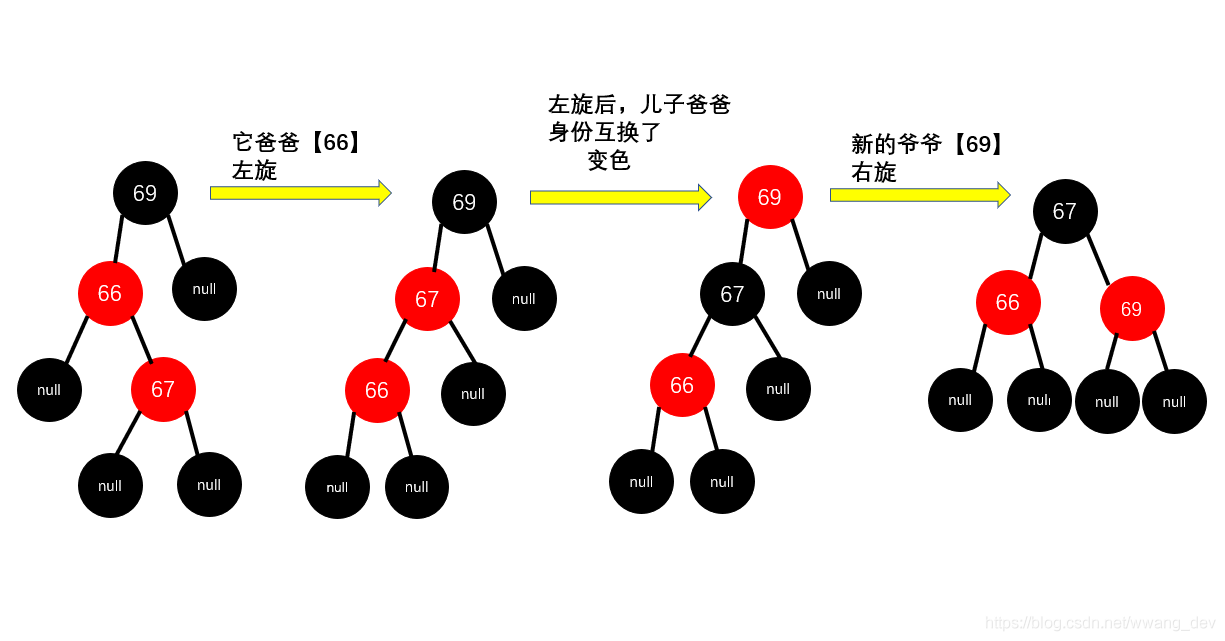
可以想一下,为什么要先左旋??
因为它的爸爸是左孩子,可是它偏偏插在了右节点的位置,那么我现在不能确定到底哪边树高,要往哪边偏,那既然它爸爸本来是左孩子,我就先向左偏,左旋完后肯定是左边树高,并且你发现没??左旋完后就和第一种情况左左插一致了,所以后续【变色+右旋】两个过程也是一样的。
3. 右左插入后旋转
这种情况下,父节点是右节点,插入的节点是左节点,
这种情况,我们要插入节点【68】
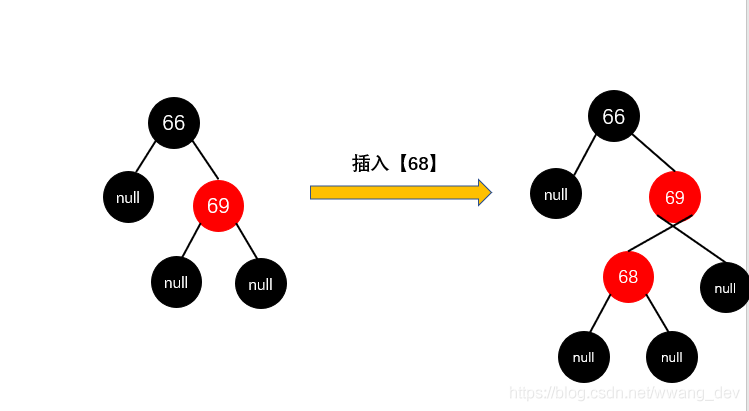
规则如下:先【旋转】使偏向一边,再【变色】解决连续红色问题,再【旋转】解决高度差问题
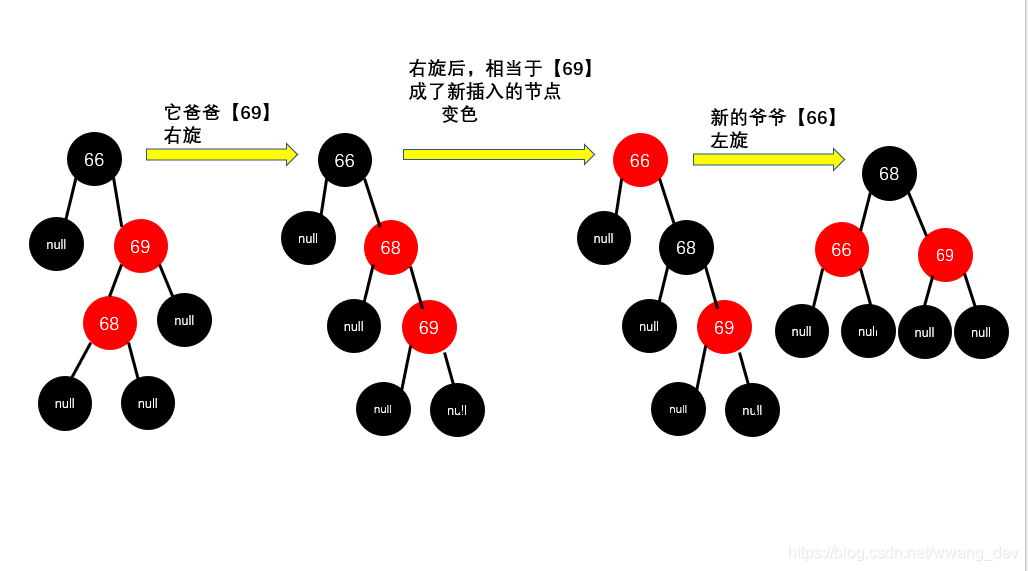
和情况2对比一下,你应该能想到,现在是爸爸是右孩子,儿子是左孩子,那么我们就先右旋,偏向右边,此时,它就变成了第四种情况(右右插),之后再【变色+左转】
- 它爸爸【69】右旋,右旋后儿子爸爸身份互换,【68】成了爸爸,【69】成了儿子,相当于【69】成了新插入的红色节点)
- 把它爸爸【68】变成黑色,把它爷爷【66】变成红色
- 它爷爷【66】左旋
4. 右右插入后旋转
这种情况下,父节点和插入的节点都是右节点,
这种情况下,我们要插入节点【70】
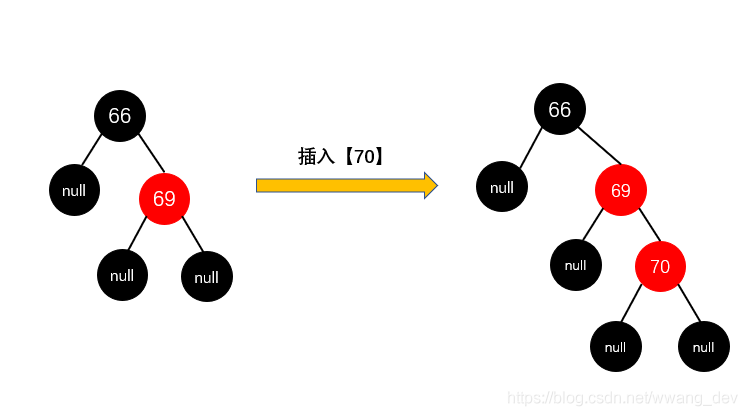
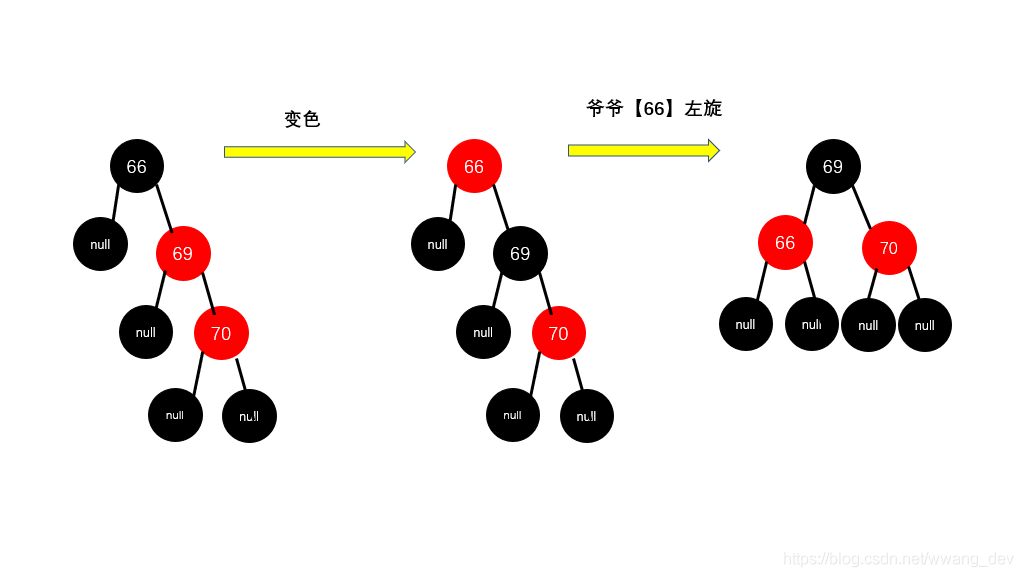
规则如下:先【变色】解决连续红色问题,再【旋转】解决高度差问题
- 把它爸爸【69】变成黑色,把它爷爷【66】变成红色
- 它爷爷【66】左旋
三、总结
左左插:
- 爸爸变黑色,爷爷变红色
- 爷爷右旋
左右插:
- 爸爸左旋,左旋之后爸爸成了儿子(也就是新插入的红色节点),之后和【左左插】一样
- 爸爸变黑色,爷爷变红色
- 爷爷右旋
右右插:
- 爸爸变黑色,爷爷变红色
- 爷爷左旋
左右插:
- 爸爸右旋,右旋之后爸爸成了儿子(也就是新插入的红色节点),之后和【右右插】一样
- 爸爸变黑色,爷爷变红色
- 爷爷左旋
我们结合之前的情形,对 put() 过程做一个推测,大概是下面这个模式:
public V put(K key, V value) {
// 1. 从根节点往下,根据二叉排序树的特点,找到新的节点应该插入的合适位置
// 2. 当找到合适位置后,根据键值大小,决定它要作为它爸爸的左孩子还是右孩子
// 3. 插入之后,修复这颗红黑树
fixAfterInsertion(e);
}
而 fixAfterInsertion() 的过程应该是这样
private void fixAfterInsertion(MyTreeMap.Entry<K,V> x) {
// 1. 新节点【51】标记为红色
x.color = RED;
// 2. 如果它的爸爸是黑色,不进行变色也不用旋转,直接返回
// 3. 如果他的爸爸是红色,而且肯定是有个循环逐步向上一直进行到根
while (x != null && x != root && x.parent.color == RED) {
// 得到它的叔叔
TreeMap.Entry<K,V> y = leftOf(parentOf(parentOf(x)));
// 3.1 如果它的叔叔也是红色,那么只需要变色不需要旋转
if (colorOf(y) == RED) {
// 把它爸爸变成黑色
setColor(parentOf(x), BLACK);
// 把它叔叔变成黑色
setColor(y, BLACK);
// 把它爷爷变成红色
setColor(parentOf(parentOf(x)), RED);
// 它跳到它爷爷的位置上,继续向上进行变色
x = parentOf(parentOf(x));
// 3.2 如果它的叔叔不是红色(也就是黑色),必须变色+旋转
} else {
// 如果它爸爸是左孩子
if(parent == leftOf(parentOf(parent))){
// 3.2.1 如果它是右孩子---对应 左右插
if(x = leftOf(parent)) {
// 它爸爸左旋,
rolateRight(parent)
// 旋转之后,儿子爸爸互换身份,之后就会变成左左插的情况,和左左插执行一样的过程
}
// 3.2.2 左左插
// 把它爸爸变成黑色
setColor(parentOf(x), BLACK);
// 把它爷爷变成红色
setColor(parentOf(parentOf(x)), RED);
// 它爷爷右旋
rotateRight(parentOf(parentOf(x)));
}
// 如果它爸爸是右孩子
else {
// 3.2.3 如果它是左孩子 ---- 对应右左插
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
// 它爸爸为右旋
rotateRight(x);
// 旋转之后,儿子爸爸互换身份,之后就会变成右右插的情况,和左左插执行一样的过程
}
// 3.2.4 右右插
// 把它爸爸变成黑色
setColor(parentOf(x), BLACK);
// 把他爷爷变成红色
setColor(parentOf(parentOf(x)), RED);
// 它爷爷左旋
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 4. 根节点强制为黑色
root.color = BLACK;
}
注意上面的代码只是我根据之前的分析提取出来的一个框架,不用追究细节
我们是先判断它叔叔是不是红色,如果不是红色就需要进行变色加旋转,再根据它爸爸和儿子的位置划分出四种旋转的情形;
而JDK1.8里面,TreeMap源码是这么干的,它是先判断它爸爸是左孩子还是右孩子,然后在两种情况下都再去判断它叔叔是不是红色,这样的话就会形成四个判断,我个人觉得它叔叔是红色的时候根本不用旋转我压根不用管它爸爸是什么位置,所以我只需要在它叔叔是黑色的时候去分四种旋转情形,不知道是我想简单了还是怎么滴。
最后,我们来看看实际的源码是如何写的吧。
public V put(K key, V value) {
// 保存根节点
MyTreeMap.Entry<K,V> t = root;
// 如果树是空的
if (t == null) {
compare(key, key); // type (and possibly null) check
// 那么当前节点直接作为根节点
root = new MyTreeMap.Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
// 定义一个临时节点,保存节点的爸爸
MyTreeMap.Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
// 我们构造一个TreeMap时可以传入一个自己实现的比较器,作为节点直接比较大小的规则
// 下面这个if和else就是根据我们是不是指定了自定义比较器来进行不同的比较规则
// 先是确定比较规则,再进行比较,代码基本一样,我们看第一部分即可
if (cpr != null) {
// 如果自己定义了比较器
do {
// 从根节点往下,根据二叉排序树的特点,找到新的节点应该插入的合适位置
parent = t;
// 比较当前节点和新的节点的键值
cmp = cpr.compare(key, t.key);
// 如果新的节点键值小于当前节点
if (cmp < 0)
// 那么我们就去当前节点的左子树中找合适位置
t = t.left;
// 如果新的节点键值比当前节点大
else if (cmp > 0)
// 我们就去当前节点的右子树中找它的合适位置
t = t.right;
// 如果新的键值和当前节点的键值相等,
else
// 则用新的节点值覆盖这个节点值,就直接返回,无后续操作
return t.setValue(value);
} while (t != null);
}
// 跳过这个else,无非是用了另一个比较器,和上面if过程差不多
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
// 当找到合适位置后,parent中保存的是它的爸爸
MyTreeMap.Entry<K,V> e = new MyTreeMap.Entry<>(key, value, parent);
// 根据键值大小,决定它要作为它爸爸的左孩子还是右孩子
if (cmp < 0)
// 作为左孩子
parent.left = e;
else
// 作为右孩子
parent.right = e;
// 插入之后,修复这颗红黑树
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
/** From CLR */
/**
* 回顾一下四种旋转情况:
* 新插入节点【x】,它爸爸是【xx】,它爷爷是【xxx】
* 1. 【xx】是【xxx】的左孩子:
* 1.1 【x】是【xx】的左孩子
变色 --> 【xxx】右旋
* 1.2.【x】是【xx】的右孩子
* 【xx】【左旋】,身份互换 --> 变色 --> 【xxx】【右旋】
* 2. 【xx】是【xxx】的右孩子:
* 2.1 【x】是【xx】的左孩子
* 【xxx】【右旋】,身份互换 --> 变色 --> 【xxx】【左旋】
* 2.2.【x】是【xx】的右孩子
* 【xxx】【左旋】
* @param x
*/
private void fixAfterInsertion(MyTreeMap.Entry<K,V> x) {
// 新节点标记为红色
x.color = RED;
// 如果它的爸爸是黑色,会跳转while,不进行变色也不用旋转,直接返回
// 如果他的爸爸是红色
while (x != null && x != root && x.parent.color == RED) {
// 如果它的爸爸是 左孩子
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// 得到它的叔叔
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
// 如果它的叔叔【也是红色,那么只需要变色不需要旋转
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK); // 把它爸爸变成黑色
setColor(y, BLACK); // 把它叔叔变成黑色
setColor(parentOf(parentOf(x)), RED); // 把它爷爷变成红色
x = parentOf(parentOf(x)); // 它跳转成它爷爷,继续向上进行变色
} else {
// 如果它是右孩子----左右插
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
// 那么它爸爸左旋,之后和 左左插步骤一样
rotateLeft(x);
}
// 左左插
// 把它爸爸变成黑色
setColor(parentOf(x), BLACK);
// 把它爷爷变成红色
setColor(parentOf(parentOf(x)), RED);
// 它爷爷右旋
rotateRight(parentOf(parentOf(x)));
}
// 如果它的爸爸是右孩子
} else {
// 得到它的叔叔
MyTreeMap.Entry<K,V> y = leftOf(parentOf(parentOf(x)));
// 如果它的叔叔也是红色,那么只需要变色,不需要旋转
if (colorOf(y) == RED) {
// 把他爸爸变成黑色
setColor(parentOf(x), BLACK);
// 把他叔叔变成黑色
setColor(y, BLACK);
// 把他爷爷变成红色
setColor(parentOf(parentOf(x)), RED);
// 它去到它爷爷的位置,继续向上重复变色过程
x = parentOf(parentOf(x));
// 他的叔叔是黑色,需要旋转+变色
} else {
// 如果它是左孩子 ---- 右左插
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
// 它爸爸右旋 身份互换,之后和 右右插步骤一样
rotateRight(x);
}
// 把它爸爸变成黑色
setColor(parentOf(x), BLACK);
// 把他爷爷变成红色
setColor(parentOf(parentOf(x)), RED);
// 它爷爷左旋
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 根节点强制为黑色
root.color = BLACK;
}
好了,今天的分享就到这里了,建议大家和第一篇博客一起看,效果会好一点,我也相信看完这两篇博客你一定能很清楚的说出来红黑树在插入一个新的节点的时候,到底是怎么样的一个过程。
下一篇博客我应该会介绍一下它的删除过程吧(不确定哦,大家可以尝试自己看看),也可以看这这篇博客,我是在此基础上加上自己的理解和总结,再结合源码写的文章,他确实写的很好。
有任何问题可以留言,谢谢!