非刚性人脸跟踪 —— 几何约束

　　面部几何参数化通常由两个因素组成：全局（刚性）变换和局部的（非刚性）形变。全局变换考虑人脸在图像中的整体位置，它经常允许人脸随意变化（即人脸可出现在图像的任何位置）。这包括人脸在图像中的 (x,y) 位置，平面内头部的旋转，脸在图像中的大小。另一方面，局部形变考虑不同人面部形状以及同一个人面部表情的差异。与全局变换相比较，这些局部变形往往更受限于面部特征的高度结构化形状。全局变换是二维坐标的常规处理，可用于任意类型的对象，而局部形变针对的是具体对象，需要从训练集中学习。

　　这节将介绍面部结构的几何模型，即形状模型。这个模型是在 shape_model 类中被实现的，该类的定义及实现可分别在 shape_model.hpp 和 shape_model.cpp 文件中找到。下面的代码是 shape_model 类在头文件的一部分，展示了该类的主要功能：

class shape_model{                         //2d linear shape model
public:
  Mat p;             // 展示模型时，将原始坐标投影到展示空间里的投影矩阵
  Mat V;             // 描述人脸模型的联合矩阵
  Mat e;             // 存在联合空间内表情模型坐标的标准差矩阵
  Mat C;             // 描述之前标注的连接关系矩阵

  void            // 将点集投影到貌似脸型的空间中，对被投影的每个点有选择的给出单独的置信权重
  calc_params(const vector<Point2f> &pts,  //points to compute parameters from
          const Mat weight = Mat(),    //weight of each point (nx1) CV_32F
          const float c_factor = 3.0); //clamping factor
          

  vector<Point2f>    // 通过解码用在人脸模型的参数向量 p（通过V和e编码）来生成点集
  calc_shape();

  void    // 从脸型数据集中学习编码模型
  train(const vector<vector<Point2f> > &p, //N-example shapes
    const vector<Vec2i> &con = vector<Vec2i>(),//point-connectivity
    const float frac = 0.95,           //fraction of variation to retain
    const int kmax = 10);              //maximum number of modes to retain
    ...    
};

1. Procrustes 分析

　　为了建立脸型的形变模型，首先必须删除原始标注数据中适用于全局刚性运行的部分。当在二维情形建立几何模型时，通常用相似变换来表示刚性运动，相似变换包括伸缩、平面内旋转、变换。下面展示了相似变换所能得到的运动类型。从点集删除全局刚性运动的过程称为 Procrustes 分析。

　　

　　在数学上，Procrustes 分析的目的是要同时找到一个标准形状和每个数据实例的相似变换，并让这些数据实例与标准形状对齐。这里用最小平方距离来度量每个经相似变换后的形状与标准形状对齐的如何。

1.  求每个样本点在 N 幅图像中的均值并进行归一化

   Mat P = X.clone();
   for(int i = 0; i < N; i++){
     Mat p = P.col(i);
     float mx = 0,my = 0;
     for(int j = 0; j < n; j++){mx += p.fl(2*j); my += p.fl(2*j+1);}
     mx /= n; my /= n;        // 计算样本点位置均值
     // 归一化，即去中心化
     for(int j = 0; j < n; j++){p.fl(2*j) -= mx; p.fl(2*j+1) -= my;}
   }

2. 根据去中心化数据，计算每幅图像中图像的比例和角度，然后旋转和缩放每个形状使之能与标准形状有最佳匹配

   for (int iter = 0; iter < itol; iter++){
       // 计算 n 个形状的重心并归一化
       Mat C = P*Mat::ones(N, 1, CV_32F) / N; normalize(C, C);
       if (iter > 0){ if (norm(C, C_old) < ftol)break; }
       C_old = C.clone();
       for (int i = 0; i < N; i++){
           // 求当前形状与归一化重心之间的旋转角度
           Mat R = this->rot_scale_align(P.col(i), C);
           for (int j = 0; j < n; j++){
               float x = P.fl(2 * j, i), y = P.fl(2 * j + 1, i);
               // 仿射变化
               P.fl(2 * j, i) = R.fl(0, 0)*x + R.fl(0, 1)*y;
               P.fl(2 * j + 1, i) = R.fl(1, 0)*x + R.fl(1, 1)*y;
           }
       }
   }　　

 　　　　

　　　　计算平面内的旋转和伸缩，这个过程是通过 rot_scale_align 函数来实现的：

Mat rot_scale_align(const Mat &src,
        const Mat &dst)
{
  //construct linear system
  int n = src.rows/2; float a=0,b=0,d=0;
  for(int i = 0; i < n; i++){
    d += src.fl(2*i) * src.fl(2*i  ) + src.fl(2*i+1) * src.fl(2*i+1);
    a += src.fl(2*i) * dst.fl(2*i  ) + src.fl(2*i+1) * dst.fl(2*i+1);
    b += src.fl(2*i) * dst.fl(2*i+1) - src.fl(2*i+1) * dst.fl(2*i  );
  }
  a /= d; b /= d;//solved linear system
  return (Mat_<float>(2,2) << a,-b,b,a);
}

　　　　此函数会计算旋转形状与标准形状之前的最小二乘。数学表示如下：　　　　

　　　　

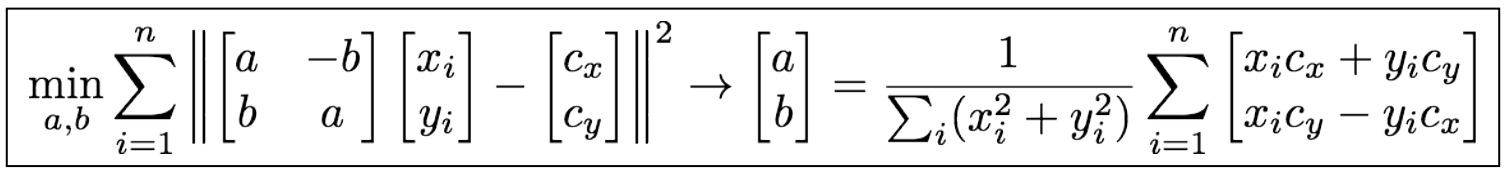
　　　　只需对变量 (a,b) 求解即可，这两个变量与伸缩旋转矩阵的关系如下：

　　　　

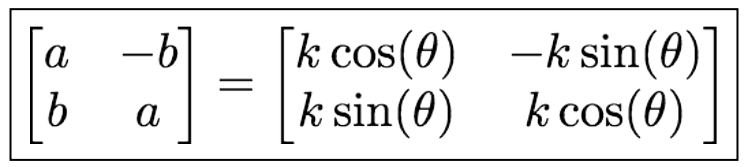
　　　　对原始标注形状进行 Procrustes 分析后，其可视化效果如下图所示。

　　　　

　　　　每个面部特征都用单独的一种颜色显示，在变换归一化后，结构变得很明显，其中面部特征的位置聚集在这些平均特征的周围。在迭代完成伸缩和旋转归一化之后，同一特征之间聚集的更加紧凑，其分布变更能反映出面部形变引起的变化。

2. 线性形状模型

　　面部形变模型的目标是找到一组少量参数来表示多个人以及不同表情的脸型是如何变化的。其中最简单的是使用面部几何的线性表示，其主要思想如下图所示。

　　

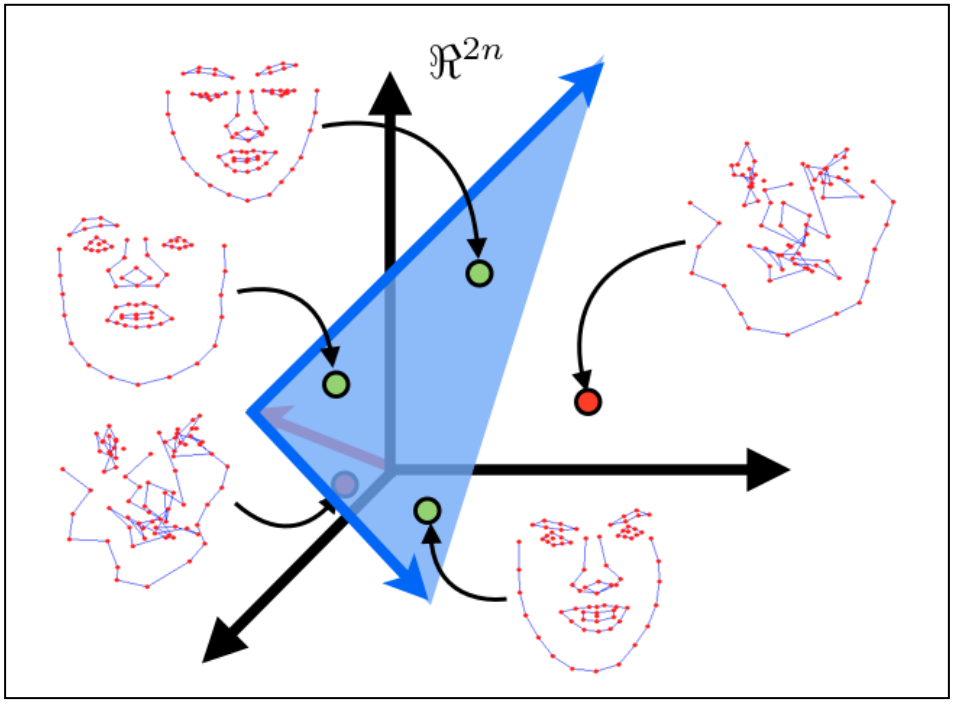
　　由 N 个面部特征构成的一幅人脸图像可看作是 2N 维空间的一个点。线性模型的目标就是找到一个低维超平面嵌入 2N 维空间，所有人脸的点（即上图中那些绿色的点）都在这个 2N 维空间中。这个超平面仅由整个 2N 维空间的一个子集生成，因此通常称它为子空间。子空间维度越低，对人脸的表示就越简洁，跟踪过程中的约束就越强，这就会得到鲁棒性更好的跟踪。但是，应注意所选择子空间的维数，既要使其有足够的能力来生成所有人脸的空间，但不能过多，使非脸型的点（即上图中红色的点）也在生成的空间中。

　　查找生成数据集的最佳低维空间的过程叫做主成分分析（ PCA ）。OpenCV 有一个类可用来计算 PCA。但需要预先指定所获得子空间的维数。因为预先得到这个维数很困难，通常用启发式方法来得到，即按所选择的特征向量对应的特征值占整个特征值的比例来确定该维数。由于样本经过预处理，已经是去中心化的数据，PCA 和 SVD 可以直接对应起来，（ PCA 得到的是矩阵 Data 的特征值，SVD 就是矩阵 Data*Data^T 特征值的平方根），因此下面的代码是用 SVD 实现的。

　　为了提取非刚性成分，我们要从预处理后的形状中剔除刚性成分。为此我们要先求 N 幅图像对齐后形状空间的标准正交基，然后将每幅图像的原始形状投射到该标准正交空间得到新的形状坐标集合，再用原始图像减去该集合得到非刚性成分。

　　函数 calc_rigid_basis 就是用来求对齐后形状空间的 Schmidt 标准正交基，代码如下：

// 求 Schmidt 标准正交基
Mat calc_rigid_basis(const Mat &X)
{
  //compute mean shape
  int N = X.cols,n = X.rows/2;
  Mat mean = X*Mat::ones(N,1,CV_32F)/N;

  //construct basis for similarity transform
  Mat R(2*n,4,CV_32F);
  for(int i = 0; i < n; i++){
    R.fl(2*i,0) =  mean.fl(2*i  ); R.fl(2*i+1,0) =  mean.fl(2*i+1);
    R.fl(2*i,1) = -mean.fl(2*i+1); R.fl(2*i+1,1) =  mean.fl(2*i  );
    R.fl(2*i,2) =  1.0;            R.fl(2*i+1,2) =  0.0;
    R.fl(2*i,3) =  0.0;            R.fl(2*i+1,3) =  1.0;
  }
  //Gram-Schmidt orthonormalization
  for(int i = 0; i < 4; i++){
    Mat r = R.col(i);
    for(int j = 0; j < i; j++){
      Mat b = R.col(j); r -= b*(b.t()*r);
    }
    normalize(r,r);
  }return R;
}

　　整个非刚性特征提取的实现代码如下：

//compute rigid transformation
Mat R = this->calc_rigid_basis(Y);

//compute non-rigid transformation
Mat P = R.t()*Y; Mat dY = Y - R*P; 
// Data = U*w*Vt ，奇异值矩阵为w
SVD svd(dY*dY.t());
int m = min(min(kmax,N-1),n-1);
float vsum = 0; for(int i = 0; i < m; i++)vsum += svd.w.fl(i);
float v = 0; int k = 0; 
// 取前 k 个奇异值
for(k = 0; k < m; k++){v += svd.w.fl(k); if(v/vsum >= frac){k++; break;}}
if(k > m)k = m;
Mat D = svd.u(Rect(0,0,k,2*n));    // 非刚性变化投影

　　w 是 openCV 的 SVD 类的成员变量，它用来存放数据主要变化方向的方差，其存储顺序由大到小。选择子空间维数的常用方法是在 w 中找一个最小集合，使该集合元素与整个数据能量的比例大于变量 frac，其中，svd.w 各元素的值就表示数据在不同方向上的能量大小。由于这些元素是从大到小依次存储的，只需简单获取前 k 个变化方向的能量就可得到要选择的子空间维数。数据变化方向本身储存在 SVD 类的成员变量 u 中。svd.w 和 svd.u 中的每个元素通常称为特征值和特征向量。这两个变量中元素之间的关系如下图所示：

　　

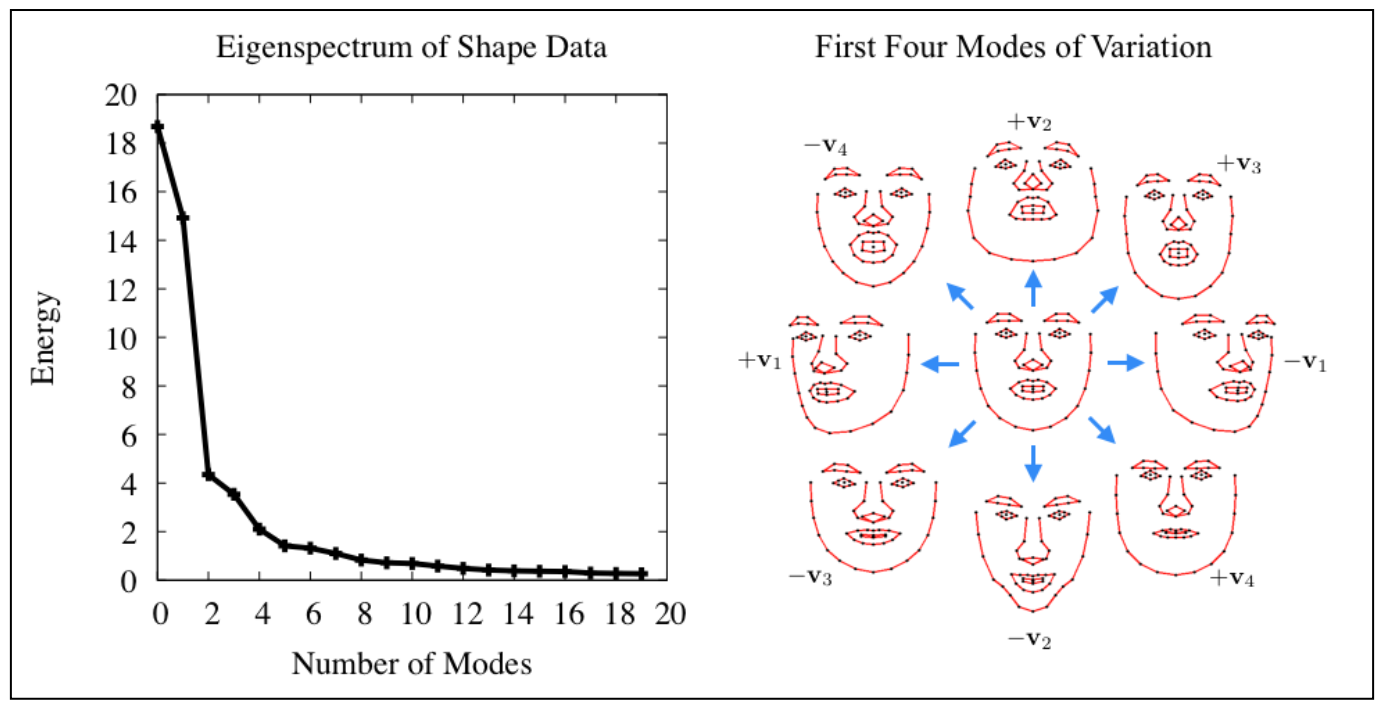
　　上图的特征值会迅速减少，这种现象暗示数据中的面部变化可用低维子空间来表示。

3. 局部-全局相结合的表示

　　一个图像帧的形状由局部形变和全局变换组合在一起得到。从数学角度来讲，这种参数化可能会产生问题，因为这些变换组合后的结果会是一个非线性函数，该函数没有闭解。要绕过这个问题的通常做法是将全局变换作为一个线性子空间，并将其加到形变自空间中。对于一个具体的人脸，其相似变换可用子空间来表示，具体表示如下：

　　

　　主要代码如下：

//combine bases
V.create(2*n,4+k,CV_32F);                     // combined subspace
Mat Vr = V(Rect(0,0,4,2*n)); R.copyTo(Vr);    // rigid subspace
Mat Vd = V(Rect(4,0,k,2*n)); D.copyTo(Vd);    // nonrigid subspace

　　由于刚性变换引起的变化方向以及从数据中删除，所产生的形变子空间会与刚性变换子空间正交。因此，可拼接两个子空间，从而得到脸型的局部-全局线性表示。从上述代码可知，联合矩阵可分为两个分块矩阵，左半边是刚性参数（4列），右半边是非刚性参数（k列）。

　　这种模型的正交性意味着描述形状的参数很容易计算：

　　　　p_(k+4)*N = V^T_2n*(K+4) * X_2n*N   

　　P 是人脸形状在联合子空间的坐标，V 是联合变化矩阵，X 是 2N 维空间样本坐标。这样就可以获得联合分布空间的坐标了。

　　主要代码如下：

//compute variance (normalized wrt scale)
Mat Q = V.t()*X;        // Q 即为联合分布空间中的新坐标集合
for(int i = 0; i < N; i++){
// 方差 v 可用来防止相对较大的数据样本影响估计
float v = Q.fl(0,i); Mat q = Q.col(i); q /= v; 
}
e.create(4+k,1,CV_32F);
pow(Q,2,Q);    // 计算方差
for(int i = 0; i < 4+k; i++){
if(i < 4)e.fl(i) = -1;    // 负值赋值给刚性子空间中坐标的方差
// 对 k 列非刚性系数，分别求每幅图像的平均
else e.fl(i) = Q.row(i).dot(Mat::ones(1,N,CV_32F))/(N-1);
}　　

　　最后要注意的是线性模型化脸型要怎么约束子空间坐标，才使生成的形状有效。在下图中，对子空间表示的人脸做这样的操作：依次对每个人脸在某个变化的方向上增加相应坐标的值，其增量为该方向上4倍的标准偏差。注意增加的量越小，得到的形状越想人脸，而增加的量越大，人脸看上去就会越糟糕。

　　

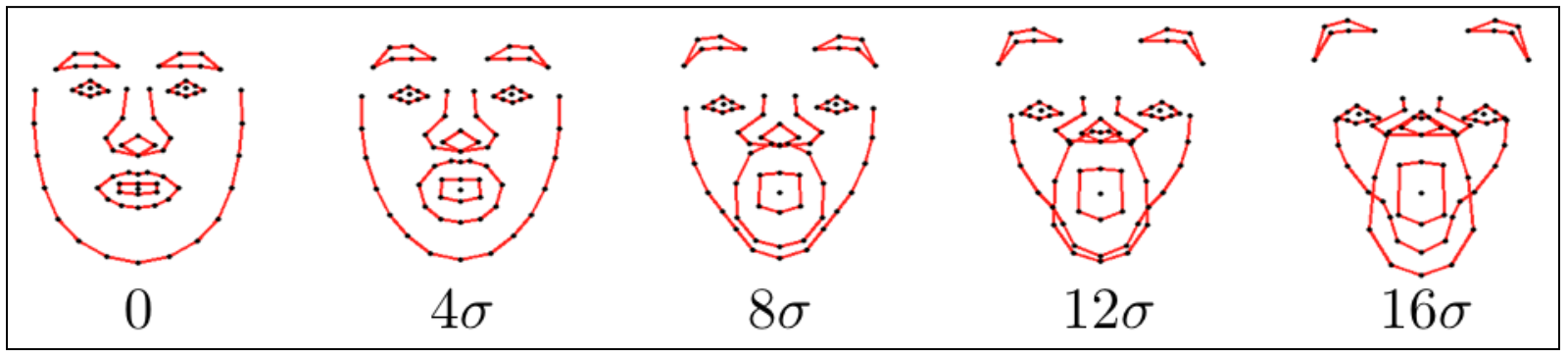
　　防止这种变形的一个简单方法是限制子空间坐标，使其只能在由数据集所决定的一个区间内。通常的做法是用 ±3 倍的数据标准偏差作为一个箱约束，这个部分占数据变化部分的 99.7%。

　　主要代码如下：

void clamp(const float c)
{
  double scale = p.fl(0);                // extract scale
  for(int i = 0; i < e.rows; i++){
    if(e.fl(i) < 0)continue;            // ignore rigid components
    float v = c*sqrt(e.fl(i));            // c*standard deviations box
    if(fabs(p.fl(i)/scale) > v){        // preserve sign of coordinate
      if(p.fl(i) > 0)p.fl(i) =  v*scale;// positive threshold
      else           p.fl(i) = -v*scale;// negative threshold
    }
  }
}

4. 训练与可视化

　　从标注数据中训练人脸模型的示例程序可从文件 train_shape_model.cpp 中找到。命令行参数 argv[1] 用来存放标注数据的路径，加载数据到内存中并删除不完整的数据后，就可开始训练。具体实现如下：

ft_data data = load_ft<ft_data>(argv[1]);
if(data.imnames.size() == 0){
    cerr << "Data file does not contain any annotations."<< endl; return 0;
}
//remove unlabeled samples and get reflections as well
data.rm_incomplete_samples();

　　每个样本的标注和相应的镜像在被传递给训练函数前会保存在一个向量中，具体实现如下：

vector<vector<Point2f> > points;
for (int i = 0; i < int(data.points.size()); i++){
    points.push_back(data.get_points(i, false));
    if (mirror)points.push_back(data.get_points(i, true));
}

　　通过函数 shape_model::train 来训练人脸模型，具体实现如下：

void
shape_model::
train(const vector<vector<Point2f> > &points,
      const vector<Vec2i> &con,
      const float frac,    // 非刚性空间奇异值的阈值  
      const int kmax)    // 非刚性空间保留奇异值的个数
{
  //vectorize points
  Mat X = this->pts2mat(points);
  int N = X.cols,n = X.rows/2;

  //align shapes
  Mat Y = this->procrustes(X);

  //compute rigid transformation
  Mat R = this->calc_rigid_basis(Y);

  //compute non-rigid transformation
  Mat P = R.t()*Y; Mat dY = Y - R*P; 
  // Data = U*w*Vt ，奇异值矩阵为w
  SVD svd(dY*dY.t());
  int m = min(min(kmax,N-1),n-1);
  float vsum = 0; for(int i = 0; i < m; i++)vsum += svd.w.fl(i);
  float v = 0; int k = 0; 
  // 取前 k 个奇异值
  for(k = 0; k < m; k++){v += svd.w.fl(k); if(v/vsum >= frac){k++; break;}}
  if(k > m)k = m;
  Mat D = svd.u(Rect(0,0,k,2*n));    // 非刚性变化投影

  //combine bases
  V.create(2*n,4+k,CV_32F);                        // combined subspace
  Mat Vr = V(Rect(0,0,4,2*n)); R.copyTo(Vr);    // rigid subspace
  Mat Vd = V(Rect(4,0,k,2*n)); D.copyTo(Vd);    // nonrigid subspace

  //compute variance (normalized wrt scale)
  Mat Q = V.t()*X;        // Q 即为联合分布空间中的新坐标集合
  for(int i = 0; i < N; i++){
    // 方差 v 可用来防止相对较大的数据样本影响估计
    float v = Q.fl(0,i); Mat q = Q.col(i); q /= v; 
  }
  e.create(4+k,1,CV_32F);
  pow(Q,2,Q);    // 计算方差
  for(int i = 0; i < 4+k; i++){
    if(i < 4)e.fl(i) = -1;    // 负值赋值给刚性子空间中坐标的方差
    // 对 k 列非刚性系数，分别求每幅图像的平均
    else e.fl(i) = Q.row(i).dot(Mat::ones(1,N,CV_32F))/(N-1);
  }
  //store connectivity
  if(con.size() > 0){ //default connectivity
    int m = con.size();
    C.create(m,2,CV_32F);
    for(int i = 0; i < m; i++){
      C.at<int>(i,0) = con[i][0]; C.at<int>(i,1) = con[i][1];
    }
  }else{              //user-specified connectivity
    C.create(n,2,CV_32S);
    for(int i = 0; i < n-1; i++){
      C.at<int>(i,0) = i; C.at<int>(i,1) = i+1;
    }    
    C.at<int>(n-1,0) = n-1; C.at<int>(n-1,1) = 0;
  }
}
//==============================================================================
Mat
shape_model::
pts2mat(const vector<vector<Point2f> > &points)
{
  int N = points.size(); assert(N > 0);
  int n = points[0].size();
  // 检查每幅图像的样本点数量是否相同
  for(int i = 1; i < N; i++)assert(int(points[i].size()) == n); 
  Mat X(2*n,N,CV_32F);
  for(int i = 0; i < N; i++){
    Mat x = X.col(i),y = Mat(points[i]).reshape(1,2*n); y.copyTo(x);
  }return X;
}

　　命令行参数 argv[2] 含有存储训练得到的人脸模型的路径，可通过下面的函数来实现存储：

save_ft(argv[2],smodel);

　　将训练所得的人脸模型储存到 shape_model.yaml ，如下图：

　　    

　　为了可视化训练得到的人脸模型，可用 visualize_shape_model.cpp 程序，它能依次展示在各个方向上所学到的非刚性形变。

　　加载脸型模型到内存，加载过程如下：

shape_model smodel = load_ft<shape_model>(argv[1]);

　　下面的方法可计算出将模型放置在窗口中心的刚性参数值：

//compute rigid parameters
int n = smodel.V.rows/2;
float scale = calc_scale(smodel.V.col(0),200);
float tranx = n*150.0/smodel.V.col(2).dot(Mat::ones(2*n,1,CV_32F));
float trany = n*150.0/smodel.V.col(3).dot(Mat::ones(2*n,1,CV_32F));

　　其中 calc_scale 函数用来查找尺度系数，该系数用 200 像素作为宽度来生成脸型。通过搜索可生成 150 个像素的平移系数来计算平移分量（即均值中心化模型，显示窗口大小为 300*300 像素）。shape_model::V 的第一列对应尺度变换，第三列和第四列分别是 x 和 y 的平移。

　　下面将生成参数值的轨迹，该轨迹从零点开始，先向正向端点移动，再向负向端点移动，然后移到零点。具体代码实现如下：

//generate trajectory of parameters
vector<float> val;
for(int i = 0; i < 50; i++)val.push_back(float(i)/50);
for(int i = 0; i < 50; i++)val.push_back(float(50-i)/50);
for(int i = 0; i < 50; i++)val.push_back(-float(i)/50);
for(int i = 0; i < 50; i++)val.push_back(-float(50-i)/50);

　　动画每阶段会变化 50 此，每次的变化量都为 0.02 。该轨迹用于展现人脸模型并将结果显示在窗口中，其具体实现如下：

//visualise
Mat img(300,300,CV_8UC3); namedWindow("shape model");
while(1){
// 根据非刚性变化，展示动画，动画数量共 V.cols-3 个
for(int k = 4; k < smodel.V.cols; k++){
    for(int j = 0; j < int(val.size()); j++){
Mat p = Mat::zeros(smodel.V.cols,1,CV_32F);
// 以下三项为固定值，以便让图像处于正中央
p.at<float>(0) = scale; p.at<float>(2) = tranx; p.at<float>(3) = trany;
// 还原脸型
p.at<float>(k) = scale*val[j]*3.0*sqrt(smodel.e.at<float>(k)); 
p.copyTo(smodel.p); img = Scalar::all(255); 
char str[256]; sprintf(str,"mode: %d, val: %f sd",k-3,val[j]/3.0);
draw_string(img,str);
// 根据结构体 p 中的信息，还原图像坐标
vector<Point2f> q = smodel.calc_shape(); 
draw_shape(img,q,smodel.C);
imshow("shape model",img);
if(waitKey(10) == 'q')return 0;
    }
}
}

　　以下为学习到的前四个人脸模型：