一、图的存储
一般来说,图的存储方式有两种:邻接矩阵和邻接表。本节只讲解邻接矩阵的形式。
设图 G(V,E) 的顶点标号为 0,1,……,N-1,那么可以令二维数组 G[N][N] 的两维分别表示图的顶点标号,即如果 G[i][j] 为 1,则说明顶点 i 和顶点 j 之间有边;如果 G[i][j] 为 0,则说明顶点 i 和顶点 j 之间不存在边,而这个二维数组 G[][] 则被称为邻接矩阵。另外,如果存在边权,则可以令 G[i][j] 存放边权,对不存在的边可以设边权为 0,-1 或是一个很大的数。如下图:
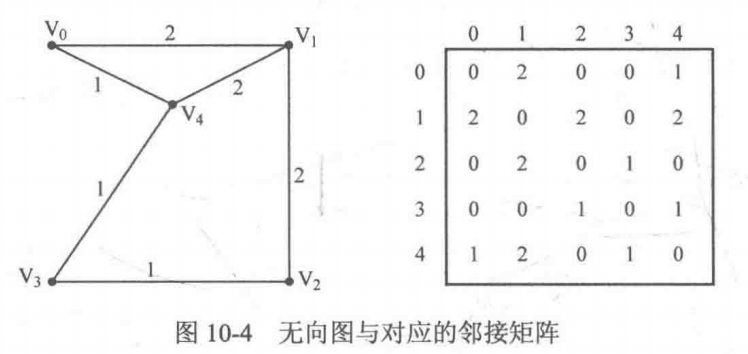
二、深度优先搜索(DFS)
深度优先搜索以“深度”作为第一关键词,每次都是沿着路径到不能再前进时才回退到最近的岔道口。
DFS 遍历图的基本思想就是将经过的顶点设置为已访问,在下次递归碰到这个顶点时就不再去处理,直到整个图的顶点都被标记为已访问。代码如下:
1 int n, G[MAXV][MAXV]; // n 为顶点数,G 为邻接矩阵 2 int vis[MAXV] = {0}; // 如果顶点 i 被访问,vis[i]=1 3 4 // u 为当前访问的顶点标号,depth 为深度 5 void DFS(int u, int depth) { 6 vis[u] = 1; // 设置顶点 u 已访问 7 int v; 8 for(v=0; v<n; ++v) { // 遍历每个顶点 9 // 若顶点 v 未被访问且可到达 10 if(!vis[v] && G[u][v] != INF) { 11 DFS(v, depth+1);// 访问 v,深度 +1 12 } 13 } 14 } 15 16 // 遍历图 G 17 void DFSTrave() { 18 int u; 19 for(u=0; u<n; ++u) { // 遍历每个顶点 20 if(!vis[u]) { // 若顶点 u 未被访问 21 DFS(u, 1); // 访问 u 以及 u 所在的连通块 22 } 23 } 24 }
三、最短路径
最短路径是图论中一个很经典的问题:给定图 G(V, E),求一条从起点到终点的路径,使得这条路径上经过的所有边的边权之和最小。
解决最短路径问题的常用算法有 Dijkstra 算法、Floyd 算法。
1. Dijkstra 算法
Dijkstra 算法用来解决单源最短路径问题,即给定图 G 和起点 s,通过算法得到 S 到达其他每个顶点的最短距离。Dijkstra 的基本思想是对图 G(V,E) 设置集合 S,存放已被访问的顶点,然后每次从集合 V-S 中选择与起点 s 的最短距离最小的一个顶点(记为 u),访问并加入集合 S。之后,令顶点 u 为中介点,优化起点从 u 能到达的顶点 v 之间的最短距离。这样的操作执行 n 次(n 为顶点个数),直到集合 S 已包含所有顶点。
为了方便编写代码,需要想办法来实现基本思想中两个较为关键的东西,即集合 S 的实现、起点 s 到达顶点 Vi (0≤i≤n-1) 的最短距离的实现。
- 集合 S 可以用一个 int 型数组 vis[] 来实现,即当 vis[i]==1 时表示顶点 Vi 已被访问,当 vis[i]==0 时表示顶点 Vi 未被访问。
- 令 int 型数组 d[] 表示起点 s 到达顶点 Vi 的最短路径,初始时除了起点 s 的 d[s] 赋为 0,其余顶点都赋为一个很大的数。
代码如下:
1 int n, G[MAXV][MAXV]; // n为顶点个数,G 为邻接矩阵 2 int vis[MAXV] = {0}; // 如果顶点 i 被访问,vis[i]=1 3 int d[MAXV]; // 起点到达各点的最短路径长度 4 5 // 求起点为 s 的最短路径长度 6 void Dijkstra(int s) { 7 int i, j; 8 for(i=0; i<MAXV; ++i) { // 初始为不可达 9 d[i] = INF; 10 } 11 d[s] = 0; // 起点到自身的距离为 0 12 for(i=0; i<n; ++i) { // n 趟 13 int u=-1, MIN=INT_MAX; // u 存放结点标号,MIN 存放最短路径长度 14 for(j=0; j<n; ++j) { 15 // 找到未访问且路径长度最短的结点 16 if(!vis[j] && d[j] < MIN) { 17 u = j; 18 MIN = d[j]; 19 } 20 } 21 if(u == -1) return; // 未找到可达结点 22 vis[u] = 1; // 标记结点 u 已访问 23 int v; 24 for(v=0; v<n; ++v) { 25 // 未访问,可达,路径长度可优化 26 if(!vis[v] && G[u][v]!=INF && d[u]+G[u][v]<d[v]) { 27 // 优化路径长度 28 d[v] = d[u]+G[u][v]; 29 } 30 } 31 } 32 }
若题目给出的是无向边,只需要把无向边当成两条指向相反的有向边即可。对邻接矩阵来说,一条 u 与 v 之间的无向边在输入时可以分别对 G[u][v] 和 G[v][u] 赋以相同的边权。
之前一直在将最短距离的求解,但是还没有讲到最短路径本身怎么求解。那么接下来学习一下最短路径的求法。
在 Dijkstra 算法中有这么一段代码:
1 int v; 2 for(v=0; v<n; ++v) { 3 // 未访问,可达,路径长度可优化 4 if(!vis[v] && G[u][v]!=INF && d[u]+G[u][v]<d[v]) { 5 // 优化路径长度 6 d[v] = d[u]+G[u][v]; 7 } 8 }
也就是说,使 d[v] 更小的方案是让 u 作为从 s 到 v 的前一个顶点(即 s→...→u→v)。这就给我们一个启发:不妨把这个信息记录下来。于是可以设置数组 pre[],令 pre[v] 表示从起点 s 到顶点 v 的最短路径上 v 的前一个顶点的编号。代码如下:
1 int n, G[MAXV][MAXV]; // n为顶点数,G 为邻接矩阵 2 int vis[MAXV] = {0}; // 如果顶点 i 被访问,vis[i]=1 3 int d[MAXV]; // 起点到达各点的最短路径长度 4 int pre[MAXV]; // 前置结点 5 6 // 求起点为 s 的最短路径长度 7 void Dijkstra(int s) { 8 int i, j; 9 for(i=0; i<MAXV; ++i) { // 初始为不可达 10 d[i] = INF; 11 pre[i] = i; // 初始状态设每个点的前驱为自身 12 } 13 d[s] = 0; // 起点到自身的距离为 0 14 for(i=0; i<n; ++i) { // n 趟 15 int u=-1, MIN=INT_MAX; // u 存放结点标号,MIN 存放最短路径长度 16 for(j=0; j<n; ++j) { 17 // 找到未访问且路径长度最短的结点 18 if(!vis[j] && d[j] < MIN) { 19 u = j; 20 MIN = d[j]; 21 } 22 } 23 if(u == -1) return; // 未找到可达结点 24 vis[u] = 1; // 标记结点 u 已访问 25 int v; 26 for(v=0; v<n; ++v) { 27 // 未访问,可达,路径长度可优化 28 if(!vis[v] && G[u][v]!=INF && d[u]+G[u][v]<d[v]) { 29 // 优化路径长度 30 d[v] = d[u]+G[u][v]; 31 pre[v] = u; // 记录 v 的前驱结点是 u 32 } 33 } 34 } 35 }
到这一步,只是求出了最短路径上每个结点的前驱,要求整条路径,需要从终止结点开始不断利用 pre[] 的信息寻找前驱,直到到达起点后从递归深处开始输出。代码如下:
1 // s 为起点坐标,v 为当前访问的顶点编号 2 void Path(int s, int v) { 3 if(s == v) { 4 printf("%d ", s); 5 return; 6 } 7 Path(s, pre[v]); // 递归访问 v 的前置结点 8 printf("%d ", v); // 从最深处 return 回来之后,输出每一层的顶点号 9 }
测试代码如下:
1 /* 2 图算法 3 */ 4 5 #include <stdio.h> 6 #include <string.h> 7 #include <math.h> 8 #include <stdlib.h> 9 #include <time.h> 10 #include <limits.h> 11 12 #define MAXV 1000 13 #define INF 0x3fffffff 14 15 int n, m, s; // 顶点个数,边数,起点编号 16 int G[MAXV][MAXV]; // G 为邻接矩阵 17 int vis[MAXV] = {0}; // 如果顶点 i 被访问,vis[i]=1 18 int d[MAXV]; // 起点到达各点的最短路径长度 19 int pre[MAXV]; // 前置结点 20 21 // u 为当前访问的顶点标号,depth 为深度 22 void DFS(int u, int depth) { 23 vis[u] = 1; // 设置顶点 u 已访问 24 printf("%d ", u); 25 int v; 26 for(v=0; v<n; ++v) { // 遍历每个顶点 27 // 若顶点 v 未被访问且可到达 28 if(!vis[v] && G[u][v] != INF) { 29 DFS(v, depth+1);// 访问 v,深度 +1 30 } 31 } 32 } 33 34 // 遍历图 G 35 void DFSTrave() { 36 memset(vis, 0, sizeof(vis)); 37 int u; 38 for(u=0; u<n; ++u) { // 遍历每个顶点 39 if(!vis[u]) { // 若顶点 u 未被访问 40 DFS(u, 1); // 访问 u 以及 u 所在的连通块 41 } 42 } 43 } 44 45 // 求起点为 s 的最短路径长度 46 void Dijkstra(int s) { 47 int i, j; 48 for(i=0; i<MAXV; ++i) { // 初始为不可达 49 d[i] = INF; 50 pre[i] = i; // 初始状态设每个点的前驱为自身 51 } 52 d[s] = 0; // 起点到自身的距离为 0 53 for(i=0; i<n; ++i) { // n 趟 54 int u=-1, MIN=INT_MAX; // u 存放结点标号,MIN 存放最短路径长度 55 for(j=0; j<n; ++j) { 56 // 找到未访问且路径长度最短的结点 57 if(!vis[j] && d[j] < MIN) { 58 u = j; 59 MIN = d[j]; 60 } 61 } 62 if(u == -1) return; // 未找到可达结点 63 vis[u] = 1; // 标记结点 u 已访问 64 int v; 65 for(v=0; v<n; ++v) { 66 // 未访问,可达,路径长度可优化 67 if(!vis[v] && G[u][v]!=INF && d[u]+G[u][v]<d[v]) { 68 // 优化路径长度 69 d[v] = d[u]+G[u][v]; 70 pre[v] = u; // 记录 v 的前驱结点是 u 71 } 72 } 73 } 74 } 75 76 // s 为起点坐标,v 为当前访问的顶点编号 77 void Path(int s, int v) { 78 if(s == v) { 79 printf("%d ", s); 80 return; 81 } 82 Path(s, pre[v]); // 递归访问 v 的前置结点 83 printf("%d ", v); // 从最深处 return 回来之后,输出每一层的顶点号 84 } 85 86 int main() { 87 int u, v, w; // 起始节点、终止结点、权值 88 scanf("%d %d %d", &n, &m, &s); // 结点个数、边个数、起点标号 89 for(u=0; u<MAXV; ++u) { 90 for(v=0; v<MAXV; ++v) { 91 G[u][v] = INF; 92 } 93 } 94 int i; 95 for(i=0; i<m; ++i) { // 输入边 96 scanf("%d %d %d", &u, &v, &w); 97 G[u][v] = w; 98 } 99 Dijkstra(s); // 求最短路径 100 for(i=0; i<n; ++i) { // 输出最短路径 101 printf("%d ", d[i]); 102 } 103 printf(" "); 104 Path(0, 5); // 求结点 0 到 5 的最短路径 105 DFSTrave(); // 深度优先搜索 106 107 return 0; 108 }
但是,更多时候从起点到终点的最短距离最小的路径不止一条,这时候,题目就会给出一个第二标尺(第一标尺是距离),要求在所有最短路径中选择第二标尺最优的一条路径。而第二标尺常见的是以下三种出题方法或其组合:
- 给每条边再增加一个边权(比如说花费),然后要求在最短路径有多条时要求路径上的花费之和最小。
- 给每个点增加一个点权(例如每个城市能收集到的物资),然后在最短路径有多条时要求路径上的点权之和最大。
- 直接问有多少条路径。
对这三种出题方法,都只需增加一个数组来存放新增的边权或点权或最短路径条数,然后在 Dijkstra 算法中修改优化 d[v] 的那个步骤即可,其他部分不需要改动。
- 新增边权。以新增的边权代表花费为例,用 cost[u][v] 表示 u→v 的花费(由题目输入),并增加一个数组 c[],c[u] 表示从起点 s 到达顶点 u 的最少花费 c[u],初始时只有 c[s] 为 0、其余 c[u] 均为 INF。代码如下:
1 // 新增边权 2 for(v=0; v<n; ++v) { 3 // 未访问,可达 4 if(!vis[v] && G[u][v]!=INF) { 5 if(d[u]+G[u][v] < d[v]) { // 以 u 为中介点可以使 d[v] 更优 6 d[v] = d[u] + G[u][v]; 7 c[v] = c[u] + cost[u][v]; 8 } else if(d[u]+G[u][v] == d[v] && c[u] + cost[u][v] < c[v]) { 9 // 最短距离相同时看是否使 c[v] 更优 10 c[v] = c[u] + cost[u][v]; 11 } 12 } 13 }
- 新增点权。以新增的点权代表城市中能收集到的物资为例,用 weight[u] 表示城市 u 中的物资数目(由题目输入),并增加一个数组 w[],w[u] 表示从起点 s 到达顶点 u 可以收集到的最大物资为 w[u],初始时只有 w[s] 为 weight[s]、其余 w[u] 均为 0。代码如下:
1 // 新增点权 2 for(v=0; v<n; ++v) { 3 // 未访问,可达 4 if(!vis[v] && G[u][v]!=INF) { 5 if(d[u]+G[u][v] < d[v]) { // 以 u 为中介点可以使 d[v] 更优 6 d[v] = d[u] + G[u][v]; 7 w[v] = w[u] + weight[v]; 8 } else if(d[u]+G[u][v] == d[v] && w[u] + weight[v] > w[v]) { 9 // 最短距离相同时看是否使 w[v] 更优 10 w[v] = w[u] + weight[v]; 11 } 12 } 13 }
- 求最短路径条数。只需要增加一个数组 num[],num[u] 表示从起点 s 到达顶点 u 的最短路径条数,初始时只有 num[s] 为 1、其余 num[u] 均为 0。代码如下:
1 // 求最短路径长度 2 for(v=0; v<n; ++v) { 3 // 未访问,可达 4 if(!vis[v] && G[u][v]!=INF) { 5 if(d[u]+G[u][v] < d[v]) { // 以 u 为中介点可以使 d[v] 更优 6 d[v] = d[u] + G[u][v]; 7 num[v] = num[u]; 8 } else if(d[u]+G[u][v] == d[v]) { 9 // 最短距离相同时累加 num 10 num[v] += num[u]; 11 } 12 } 13 }
2. Floyd 算法
Floyd 算法用来解决全源最短路径问题,即给定的图 G(V,E),求任意两点 u,v 之间的最短路径长度,时间复杂度为 O(n3)。
该算法基于这样一个事实:如果存在顶点 k,使得以 k 作为中介时顶点 i 和顶点 j 的当前最短距离缩短,则使用顶点 k 作为顶点 i 和顶点 j 的中介点,即当 dis[i][k] + dis[k][j] < dis[i][j] 时,令 dis[i][j] = dis[i][k] + dis[k][j](其中 dis[i][j] 表示从顶点 i 到顶点 j 的最短距离)。代码如下:
1 /* 2 图_Floyd 算法 3 */ 4 5 #include <stdio.h> 6 #include <string.h> 7 #include <math.h> 8 #include <stdlib.h> 9 #include <time.h> 10 11 #define INF 0x3fffffff 12 #define MAXV 200 13 int n, m; // n 为顶点数,m 为边数 14 int dis[MAXV][MAXV]; // dis[i][j] 表示从顶点 i 到顶点 j 的最短距离 15 16 void Floyd() { 17 int i, j, k; 18 for(k=0; k<n; ++k) { 19 for(i=0; i<n; ++i) { 20 for(j=0; j<n; ++j) { 21 if(dis[i][k]!=INF && dis[k][j]!=INF && dis[i][k]+dis[k][j]<dis[i][j]) { 22 dis[i][j] = dis[i][k]+dis[k][j]; // 找到最短的路径 23 } 24 } 25 } 26 } 27 } 28 29 int main() { 30 int u, v, w; 31 scanf("%d %d", &n, &m); // 输入顶点数、边数 32 int i, j; 33 for(i=0; i<n; ++i) { // 初始化 dis 数组 34 for(j=0; j<n; ++j) { 35 dis[i][j] = INF; 36 } 37 dis[i][i] = 0; 38 } 39 for(i=0; i<m; ++i) { // 输入边数据 40 scanf("%d %d %d", &u, &v, &w); 41 dis[u][v] = w; 42 } 43 Floyd(); // Floyd 算法 44 for(i=0; i<n; ++i) { // 输出最短路径长度 45 for(j=0; j<n; ++j) { 46 if(dis[i][j] != INF) { 47 printf("%d ", dis[i][j]); 48 } else { 49 printf("INF "); 50 } 51 } 52 printf(" "); 53 } 54 55 return 0; 56 }
四、最小生成树
最小生成树是在一个给定的无向图 G(V, E) 中求一棵树 T,使得这棵树拥有图 G 中的所有顶点,且所有边来自图 G 中的边,并满足整棵树的边权之和最小。
1. prim 算法
prim 算法用来解决最小生成树问题,其基本思想是对图 G(V, E) 设置集合 S,存放已被访问的顶点,然后每次从集合 V-S 中选择与集合 S 的最短距离最小的一个顶点(记为 u),访问并放入集合 S。之后,令顶点 u 为中介点,优化所有从 u 能到达的顶点 v 与集合 S 之间的最短距离。这样的操作执行 n 次(n 为顶点个数),直到集合 S 已包含所有顶点。
该算法需要实现两个关键的概念,即集合 S 的实现、顶点 Vi(0≤i≤n-1)与集合 S 的最短距离。
- 集合 S 的实现与 Dijkstra 中相同,即使用一个 int 型数组 vis[] 表示顶点是否已经被访问。其中 vis[i] == 1 表示顶点 Vi 已被访问,为 0 则表示未被访问。
- 不妨令 int 型数组 d[] 来存放顶点 Vi 与集合 S 的最短距离。初始时除了起点 s 的 d[s] 赋为 0,其余顶点都赋为一个很大的数,即不可达。
可以发现,prim 算法与 Dijkstra 算法使用的思想几乎完全相同,只有在数组 d[] 的含义上有所区别。代码如下:
1 /* 2 图_Prim 算法 3 */ 4 5 #include <stdio.h> 6 #include <string.h> 7 #include <math.h> 8 #include <stdlib.h> 9 #include <time.h> 10 11 #define MAXV 1000 12 #define INF 0x3fffffff 13 14 int n, m, G[MAXV][MAXV]; // n 为顶点数,m 为边数 15 int d[MAXV]; // 顶点与集合 S 的最短距离 16 int vis[MAXV] = {0}; // 标记是否已访问 17 18 // 默认 0 号为起始点,返回最小生成树的权值之和 19 int prim() { 20 int i, j; 21 d[0] = 0; // 初始化 d 数组 22 for(i=1; i<n; ++i) { // 除了自身,其它结点不可达 23 d[i] = INF; 24 } 25 int ans = 0; // 记录权值之和 26 for(i=0; i<n; ++i) { // n 趟 27 int u=-1, MIN=INF; // 最小值的下标,最小值 28 for(j=0; j<n; ++j) { 29 // 未访问且权值更小 30 if(!vis[j] && d[j]<MIN) { 31 u = j; 32 MIN = d[j]; 33 } 34 } 35 if(u == -1) return -1; // 剩下的结点与 S 不连通 36 vis[u] = 1; // 标记结点 u 已访问 37 ans += d[u]; // 将最小的边加入最小生成树 38 int v; 39 for(v=0; v<n; ++v) { // 以 u 为中介点优化最小权值 40 // 未访问,可达,可优化 41 if(!vis[v] && G[u][v]!=INF && G[u][v]<d[v]) { 42 d[v] = G[u][v]; 43 } 44 } 45 } 46 return ans; 47 } 48 49 int main() { 50 int u, v, w; 51 scanf("%d %d", &n, &m); // 顶点个数,边个数 52 int i, j; 53 for(i=0; i<n; ++i) { // 初始化图 G 54 for(j=0; j<n; ++j) { 55 G[i][j] = INF; 56 } 57 } 58 for(i=0; i<m; ++i) { 59 scanf("%d %d %d", &u, &v, &w); 60 G[u][v] = G[v][u] = w; // 无向图 61 } 62 int ans = prim(); // Prim 算法 63 printf("%d ", ans); 64 65 return 0; 66 }
2. kruskal 算法
kruskal 算法的基本思想为:在初始状态时隐去图中的所有边,这样图中每个顶点都自成一个连通块。之后执行下面的步骤:
- 对所有边按边权从小到大进行排序。
- 按边权从小到大测试所有边,如果当前测试边所连接的两个顶点不在同一个连通块中,把这条测试边加入当前最小生成树中;否则,将边舍弃。
- 执行步骤 2,,直到最小生成树中的边数等于总顶点数减 1 或是测试完所有边时结束。而当结束时如果最小生成树的边数小于总顶点数减 1,说明该图不连通。
下面来解决代码实现的问题。
首先是边的定义。对 kruskal 算法,由于需要判断边的两个端点是否在不同的连通块中,因此边的两个端点的编号一定是需要的;而算法中又涉及边权,因此边权也必须要有。于是定义如下:
1 // 边定义 2 typedef struct { 3 int u, v; // 端点编号 4 int cost; // 边权 5 } edge; 6 edge E[MAXE]; // 边集
还需要自定义 qsort 函数的 cmp 函数,让数组 E 按边权从小到大排序:
1 // 自定义排序 2 int cmp(const void* a, const void* b) { 3 edge* c = (edge*)a; 4 edge* d = (edge*)b; 5 return c->cost - d->cost; 6 }
还有两个细节似乎不太直观,即
- 如何判断测试边的两个端点是否在不同的连通块中。
- 如何将测试边加入最小生成树中。
如果把每个连通块当作一个集合,那么就可以把问题转换为判断两个端点是否在同一个集合中,这可以用并查集。并查集可以通过查询两个结点所在集合的根结点是否相同来判断它们是否在同一个集合,而合并功能恰好可以把上面提到的第二个细节解决,即只要把测试边的两个端点所在集合合并,就能达到将边加入最小生成树的效果。
1 int father[MAXV]; // 并查集数组 2 3 // 并查集查找根结点 4 int findFather(int x) { 5 int a = x; // 保存原结点 6 while(x != father[x]) { // 寻找根结点 7 x = father[x]; 8 } 9 // 重新走一遍寻找根结点的过程 10 while(a != father[a]) { 11 int z = a; // 保存结点 a 12 a = father[a]; // 回溯父亲结点 13 father[z] = x; // 将所有结点的父亲改为根结点 x 14 } 15 16 return x; // 返回根结点 17 } 18 19 // n 为点数,m 为边数,返回最小生成树的边权之和 20 int krustal(int n, int m) { 21 // ans 为边权之和, Num_Edge 为当前生成树的边数 22 int ans=0, Num_Edge=0; 23 int i; 24 for(i=0; i<n; ++i) { 25 father[i] = i; // 并查集初始化 26 } 27 // 按权值从小到大排序 28 qsort(E, m, sizeof(E[0]), cmp); 29 for(i=0; i<m; ++i) { 30 int faU = findFather(E[i].u); // 查询端点所在集合的根结点 31 int faV = findFather(E[i].v); 32 if(faU != faV) { // 不在同一集合 33 father[faU] = faV; // 合并集合 34 ans += E[i].cost; // 边权之和 35 Num_Edge++; // 当前生成树边数加 1 36 if(Num_Edge == n-1) break; 37 } 38 } 39 if(Num_Edge != n-1) return -1; // 有多个连通块 40 else return ans; // 返回最小生成树的边权之和 41 }
测试代码如下:
1 /* 2 图_Krustal 算法 3 */ 4 5 #include <stdio.h> 6 #include <string.h> 7 #include <math.h> 8 #include <stdlib.h> 9 #include <time.h> 10 11 #define MAXV 110 12 #define MAXE 10010 13 14 // 边定义 15 typedef struct { 16 int u, v; // 端点编号 17 int cost; // 边权 18 } edge; 19 edge E[MAXE]; // 边集 20 21 int father[MAXV]; // 并查集数组 22 23 // 自定义排序 24 int cmp(const void* a, const void* b) { 25 edge* c = (edge*)a; 26 edge* d = (edge*)b; 27 return c->cost - d->cost; 28 } 29 30 // 并查集查找根结点 31 int findFather(int x) { 32 int a = x; // 保存原结点 33 while(x != father[x]) { // 寻找根结点 34 x = father[x]; 35 } 36 // 重新走一遍寻找根结点的过程 37 while(a != father[a]) { 38 int z = a; // 保存结点 a 39 a = father[a]; // 回溯父亲结点 40 father[z] = x; // 将所有结点的父亲改为根结点 x 41 } 42 43 return x; // 返回根结点 44 } 45 46 // n 为点数,m 为边数,返回最小生成树的边权之和 47 int krustal(int n, int m) { 48 // ans 为边权之和, Num_Edge 为当前生成树的边数 49 int ans=0, Num_Edge=0; 50 int i; 51 for(i=0; i<n; ++i) { 52 father[i] = i; // 并查集初始化 53 } 54 // 按权值从小到大排序 55 qsort(E, m, sizeof(E[0]), cmp); 56 for(i=0; i<m; ++i) { 57 int faU = findFather(E[i].u); // 查询端点所在集合的根结点 58 int faV = findFather(E[i].v); 59 if(faU != faV) { // 不在同一集合 60 father[faU] = faV; // 合并集合 61 ans += E[i].cost; // 边权之和 62 Num_Edge++; // 当前生成树边数加 1 63 if(Num_Edge == n-1) break; 64 } 65 } 66 if(Num_Edge != n-1) return -1; // 有多个连通块 67 else return ans; // 返回最小生成树的边权之和 68 } 69 70 int main() { 71 int n, m; // 点数,边数 72 scanf("%d %d", &n, &m); 73 int i; 74 for(i=0; i<m; ++i) { 75 edge t; 76 scanf("%d %d %d", &t.u, &t.v, &t.cost); 77 E[i] = t; 78 } 79 int ans = krustal(n, m); 80 printf("%d ", ans); 81 82 return 0; 83 }
输入:
6 10 0 1 4 0 4 1 0 5 2 1 2 1 1 5 3 2 3 6 2 5 5 3 4 5 3 5 4 4 5 3
输出:
11