一、什么是动态规划
动态规划(DP)是一种用来解决一类最优化问题的算法思想。简单来说,动态规划将一个复杂的问题分解成若干个子问题,通过综合子问题的最优解来得到原问题的最优解。
二、动态规划的递归写法
以斐波那契(Fibonacci) 数列为例,斐波那契数列的定义为 F0=1,F1=1,Fn=Fn-1+Fn-2 (n≥2)。为了避免重复计算,可以开一个一维数组 dp,用以保存已经计算过的结果。代码如下:
1 int dp[maxn]; 2 // 斐波那契数列递归写法 3 int F(int n) { 4 if(n == 0 || n==1) return 1; // 递归边界 5 if(dp[n] != -1) return dp[n]; // 已经计算过 6 else { 7 dp[n] = F(n-1) + F(n-2); // 计算F(n),并保存 8 return dp[n]; // 返回 F(n) 结果 9 } 10 }
三、 动态规划的递归写法
以经典的数塔问题为例,如下图所示,将一些数字排成数塔的形状,其中第一层有一个数字,第二层有两个数字……第 n 层有 n 个数字。现在要从第一层走到第 n 层,每次只能走向下一层连接的两个数字中的一个,问:最后将路径上所有数字相加后得到的和最大是多少?
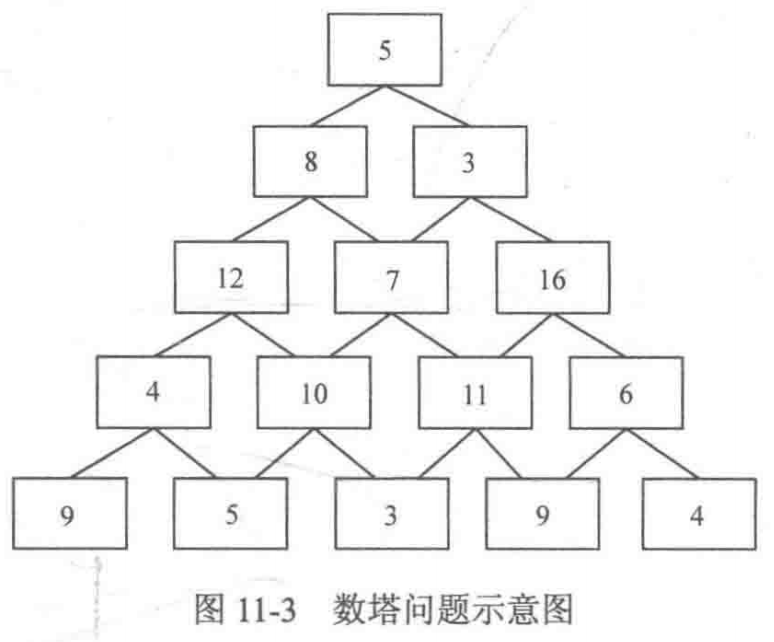
不妨令 dp[i][j] 表示从第 i 行第 j 个数字出发到达最底层的所有路径中能得到的最大和,在定义了这个数组后,dp[1][1] 就是最终想要的答案。
如果想求出 dp[i][j],那么一定要先求出它的两个子问题“从位置 (i+1,j) 到达最底层的最大和 dp[i+1][j]”和“从位置 (i+1,j+1) 到达最底层的最大和 dp[i+1][j+1]”,即进行了一次决策:走左下还是右下。写成式子就是:
dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + f[i][j]
其中 f[i][j] 存放第 i 层的第 j 个数字。代码如下:
1 /* 2 动态规划的递推写法 3 */ 4 5 #include <stdio.h> 6 #include <string.h> 7 #include <math.h> 8 #include <stdlib.h> 9 #include <time.h> 10 #include <stdbool.h> 11 12 #define maxn 1000 13 int f[maxn][maxn], dp[maxn][maxn]; 14 15 // 较大值 16 int max(int a, int b) { 17 return a>b ? a : b; 18 } 19 20 int main() { 21 int n; 22 scanf("%d", &n); 23 int i, j; 24 for(i=1; i<=n; ++i) { 25 for(j=1; j<=i; ++j) { 26 scanf("%d", &f[i][j]); // 输入数塔 27 } 28 } 29 // 边界 30 for(j=1; j<=n; ++j) { 31 dp[n][j] = f[n][j]; 32 } 33 // 从第 n-1 层往上计算 dp[i][j] 34 for(i=n-1; i>=1; --i) { 35 for(j=1; j<=i; ++j) { 36 dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + f[i][j]; 37 } 38 } 39 printf("%d ", dp[1][1]); // dp[1][1] 即为需要的答案 40 41 return 0; 42 }
下面指出两对概念的区别:
1. 分治与动态规划。分治和动态规划都是将问题分解为子问题,然后合并子问题的解得到原问题的解。但是不同的是,分治法分解出的子问题是不重叠的,因此分治法解决的问题不拥有重叠子问题,而动态规划解决的问题拥有重叠子问题。另外,分治法解决的问题不一定是最优化问题,而动态规划解决的问题一定是最优化问题。
2. 贪心与动态规划。贪心和动态规划都要求原问题必须拥有最优子结构。二者的区别在于,贪心法通过一种策略直接选择一个子问题去求解,没被选择的子问题就不去求解了,直接抛弃。也就是说,它总是只在上一步选择的基础上继续选择,因此整个过程以一种单链的流水方式进行。而动态规划总是从边界开始向上得到目标问题的解。也就是说,它总是会考虑所有子问题,并选择继承能得到最优结果的那个,对暂时没被继承的子问题,由于重叠子问题的存在,后期可能会再次考虑它们,因此还有机会成为全局最优的一部分,不需要放弃。