题意
题目描述
Kiana最近沉迷于一款神奇的游戏无法自拔。
简单来说,这款游戏是在一个平面上进行的。
有一架弹弓位于((0,0))处,每次Kiana可以用它向第一象限发射一只红色的小鸟,小鸟们的飞行轨迹均为形如(y=ax^2+bx)的曲线,其中(a,b)是Kiana指定的参数,且必须满足(a<0),(a,b)都是实数。
当小鸟落回地面(即(x)轴)时,它就会瞬间消失。
在游戏的某个关卡里,平面的第一象限中有(n)只绿色的小猪,其中第(i)只小猪所在的坐标为(left(x_i,y_i ight))。
如果某只小鸟的飞行轨迹经过了(left( x_i, y_i ight)),那么第(i)只小猪就会被消灭掉,同时小鸟将会沿着原先的轨迹继续飞行;
如果一只小鸟的飞行轨迹没有经过(left( x_i, y_i ight)),那么这只小鸟飞行的全过程就不会对第(i)只小猪产生任何影响。
例如,若两只小猪分别位于((1,3))和((3,3)),Kiana可以选择发射一只飞行轨迹为(y=-x^2+4x)的小鸟,这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的,就是通过发射小鸟消灭所有的小猪。
这款神奇游戏的每个关卡对Kiana来说都很难,所以Kiana还输入了一些神秘的指令,使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。
假设这款游戏一共有(T)个关卡,现在Kiana想知道,对于每一个关卡,至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算,所以希望由你告诉她。
输入输出格式
输入格式:
第一行包含一个正整数(T),表示游戏的关卡总数。
下面依次输入这(T)个关卡的信息。每个关卡第一行包含两个非负整数(n,m),分别表示该关卡中的小猪数量和Kiana输入的神秘指令类型。接下来的(n)行中,第(i)行包含两个正实数(x_i,y_i),表示第(i)只小猪坐标为((x_i,y_i))。数据保证同一个关卡中不存在两只坐标完全相同的小猪。
如果(m=0),表示Kiana输入了一个没有任何作用的指令。
如果(m=1),则这个关卡将会满足:至多用(lceil n/3 + 1 ceil)只小鸟即可消灭所有小猪。
如果(m=2),则这个关卡将会满足:一定存在一种最优解,其中有一只小鸟消灭了至少(lfloor n/3 floor)只小猪。
保证(1leq n leq 18),(0leq m leq 2),(0<x_i,y_i<10),输入中的实数均保留到小数点后两位。
上文中,符号(lceil c ceil)和(lfloor c floor)分别表示对(c)向上取整和向下取整,例如(lceil 2.1 ceil = lceil 2.9 ceil = lceil 3.0 ceil = lfloor 3.0 floor = lfloor 3.1 floor = lfloor 3.9 floor = 3)。
输出格式:
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数,表示相应的关卡中,消灭所有小猪最少需要的小鸟数量。
输入输出样例
输入样例#1:
2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00
输出样例#1:
1
1
输入样例#2:
3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00
输出样例#2:
2
2
3
输入样例#3:
1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99
输出样例#3:
6
说明
【样例解释1】
这组数据中一共有两个关卡。
第一个关卡与【问题描述】中的情形相同,(2)只小猪分别位于((1.00,3.00))和((3.00,3.00)),只需发射一只飞行轨迹为(y=-x^2+4)的小鸟即可消灭它们。
第二个关卡中有(5)只小猪,但经过观察我们可以发现它们的坐标都在抛物线(y=-x^2+6)上,故Kiana只需要发射一只小鸟即可消灭所有小猪。
【数据范围】
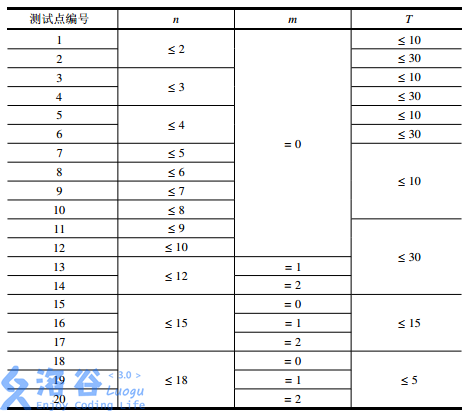
思路
我把去年的题做了下,感觉还好,动态规划不太会,而且这题好难。 --金总 2017.11.11
首先解决一个问题:对于二次函数(y=ax^2+bx),因为其中有两个系数,所以两个点就可以确定这个函数中(a,b)的值:
相互消元得:
贪心地想,我们要想用最少的鸟去击杀所有的猪,那么每只鸟击杀的猪要尽量多。我们枚举每只鸟击杀的猪的其中两头,就可以得到其发射线路的二次函数,从而算出还有哪些猪也在该条函数上。
当然,有两个特例:
- 若当前只剩下一只猪,那么这头猪必须用一只鸟来打,不能也不需要计算出鸟发射的二次函数。
- 若当前的剩下的所有猪都无法“一鸟二猪”,那么我们就用一只鸟打一只猪。
哪些情况下所有的猪都无法“一鸟二猪”呢?首先,题目要求(a>0),那么如果我们算出来(a<0)也就是二次函数开口向下,那么这样的函数是不可行的;其次,在上面的的方程中,分母部分有(x_i-x_j),而且显然横坐标相同的两点不可能出现在同一条二次函数上(通过函数的定义),所以当(x_i=x_j)时,不可行。若所有的情况都归于不可行的情况时,当前就无法“一鸟二猪”了。
当然,这样的搜索时拿不了满分的,我们考虑加上这三条来优化其时间:
- 对于当前场上存活的猪的状况,我们用一个二进制数(state)来表示。(state)上的第(k)位若为(0),表示第(k)只猪未被击杀;若为(1),表示第(k)只猪已被击杀,我们接下来的搜索中只击杀未击杀的猪。
- 记忆化一:记录数组(bin[i][j])记录击杀了(i,j)两只猪的同时可以击杀的猪。同样的,我们用一个二进制数来记录:(bin[i][j])上的第(k)位若为(0),表示第(k)只猪不可被击杀;若为(1),表示第(k)只猪可被击杀。
- 记忆化二:对于每一个(state)我们可能会多次搜索到。为了排除冗余搜索,我们记录(remember[state])表示在(state)状态下再发射(remember[state])只鸟就可以击杀所有的猪,我们就可以边搜索边记录,然后统计(remember)的值。
对于记忆化一,我们可以这么写:
void calc(double a,double b)//已经通过上面公式算出来的a和b
{
vector<int>V;//开一个vector储存可以击杀的猪
int state=0;//记录bin
for(int i=0;i<n;i++)
if(fabs(a*x[i]*x[i]+b*x[i]-y[i])<=0.000001)//注意精度判断
{
state|=(1<<i);//或运算在二进制上填1
V.push_back(i);//放入vector中
}
for(int i=0;i<V.size();i++)
for(int j=i+1;j<V.size();j++)
bin[V[i]][V[j]]=bin[V[j]][V[i]]=state;//修改bin值
}
而主要的dfs过程就是这样的:
int dfs(int state)//当前壮态为state
{
if(remember[state]!=-1) return remember[state];//已经搜索过了,直接返回
remember[state]=0x3f3f3f3f;//记录remember状态
for(int i=0;i<n;i++)
{
if(state&(1<<i)) continue;//这只猪已经死了
bool flag=false;//判断有没有猪可以和它一起被杀掉
for(int j=0;j<n;j++)
if((state&(1<<j))==0&&x[i]!=x[j]&&(x[j]*y[i]-x[i]*y[j])/(x[i]*x[j]*(x[i]-x[j]))<0.0)//判断是否可行
{
flag=true;//有猪可以和它一起被杀
if(bin[i][j]==-1) calc((x[j]*y[i]-x[i]*y[j])/(x[i]*x[j]*(x[i]-x[j])),(x[i]*x[i]*y[j]-x[j]*x[j]*y[i])/(x[i]*x[j]*(x[i]-x[j])));//运用上面的方程(说实话有点丑)
remember[state]=min(remember[state],dfs(state|bin[i][j])+1);//更新remember为最优解
}
if(!flag) return remember[state]=dfs(state|(1<<i))+1;//这只猪只能自己被杀,所以remember[state]=remember[state|(1<<i)]+1,直接更新
}
return remember[state];//搜索结束,溜了溜了
}
这样就能(AC)辣。
AC代码
#include<bits/stdc++.h>
using namespace std;
int T,n,m,ans,bin[20][20],remember[1<<18];
double x[20],y[20];
void init()
{
cin>>n>>m;
ans=INT_MAX;
for(int i=0;i<n;i++) cin>>x[i]>>y[i];
memset(bin,-1,sizeof bin);
memset(remember,-1,sizeof remember);
remember[(1<<n)-1]=0;
}
void calc(double a,double b)
{
vector<int>V;
int state=0;
for(int i=0;i<n;i++)
if(fabs(a*x[i]*x[i]+b*x[i]-y[i])<=0.000001)
{
state|=(1<<i);
V.push_back(i);
}
for(int i=0;i<V.size();i++)
for(int j=i+1;j<V.size();j++)
bin[V[i]][V[j]]=bin[V[j]][V[i]]=state;
}
int dfs(int state)
{
if(remember[state]!=-1) return remember[state];
remember[state]=0x3f3f3f3f;
for(int i=0;i<n;i++)
{
if(state&(1<<i)) continue;
bool flag=false;
for(int j=0;j<n;j++)
if((state&(1<<j))==0&&x[i]!=x[j]&&(x[j]*y[i]-x[i]*y[j])/(x[i]*x[j]*(x[i]-x[j]))<0.0)
{
flag=true;
if(bin[i][j]==-1) calc((x[j]*y[i]-x[i]*y[j])/(x[i]*x[j]*(x[i]-x[j])),(x[i]*x[i]*y[j]-x[j]*x[j]*y[i])/(x[i]*x[j]*(x[i]-x[j])));
remember[state]=min(remember[state],dfs(state|bin[i][j])+1);
}
if(!flag) return remember[state]=dfs(state|(1<<i))+1;
}
return remember[state];
}
int main()
{
cin>>T;
while(T--)
{
init();
printf("%d
",dfs(0));
}
return 0;
}