迭代法-二分迭代求解低阶线性方程

  还是用迭代法求解一个方程题，f(x)=0,如果f(x1)<0,f(x2)>0，如果f(x)是连续的，则在x1和x2

之间一定有一个值x~,使得f(x~)=0。首先用步骤描述解题框架：

1、任意找两个点x1、x2,使得f(x1)<0,f(x2)>0

2、计算x1、x2的中间点的值mid=(x1+x2)/2

3、计算f(mid),如果f(mid)>0，则最终的结果值在 x1,mid之间，将x2赋值为mid,继续1、2、3、4步骤；

如果f(mid)<0,则最终的结果值在mid,x2之间，将x1赋值为mid,继续1，2，3，4步骤

4、计算|x1-x2|是否小于某个精确度值，如果小于的话直接返回mid值，表示在该精确度范围内已经找到了

近似的解了。

如下图 f(x)=x^2-5的方程图，按照上述步骤计算f(x)=0的解

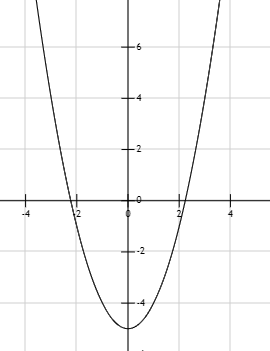
首先f(0)<0,f(4)>0,就选定0、4为初始的x1,x2来计算解，精确度定位1e-9，代码如下：

public static void main(String[] args){
    System.out.println(calculate(0,4,1e-9));
}
public static double calculate(double x1,double x2,double precision){
    double mid=(x1+x2)/2;
    while(Math.abs(x1-x2)>precision){
        if(calculate(x2)*calculate(mid)>0){
            x2=mid;
        }else{
            x1=mid;
        }
        mid=(x1+x2)/2;
    }
    return mid;
}
public static double calculate(double x){
    return 2*x*x-5;
}

输出结果：1.58113883016631

总结：迭代就是先确定一个值为初始值，然后以这个初始值为新的变量带入计算规则，将计算出的再作为新

的变量带入计算规则（函数，也就是方程），最后满足条件的话直接返回结果。