Opencv下双线性插值法进行图像放缩

关于图像放缩的算法有很多，本文主要介绍双线性插值法进行图像放缩，本文参考了： http://www.cnblogs.com/funny-world/p/3162003.html

我们设源图像src的大小为m*N，目标图像的大小为a*b。无论是放大还是缩小，我们所遵循的原则就是对于目标图像的像素点 f(i,j)，我们在源图像当中找到其对应点 f(x,y)。

其算法为：i/x=m/a  j/y=n/b 因此我们可以得到：x=i*(m/a)     y=j*(n/b)

但是为了使放缩的效果更好，可以使两个图片的几何中心重合，所以我们可以：x=(i+0.5)*(m/a)-0.5   y=(j+0.5)*(n/b)-0.5

通过这样算法，我们便可以在源图像当中找到目标图像的对应点了，但是这样计算 x,y 很可能是float型，因此我们需要继续对 x,y进行处理

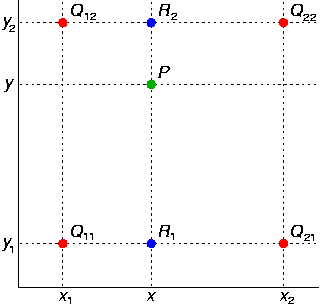
我们可以找到 于P（所求的点）最为临近的四个点 Q₁₁ ,Q₁₂ ,Q₂₁,Q₂₂ ，通过下面的算法进行处理：

 f(R₁)=(X₂-X)/(X₂-X1)*f(Q₁₁)+(X-X₁)/(X₂-X₁)*f(Q₂₁)

 f(R₂)=(X₂-X)/(X₂-X₁)*f(Q₁₂)+(X-X₁)/(X₂-X₁)*f(Q₂₂)

 f(i,j)=(Y₂-Y)/(Y₂-Y1)f(R₁)+(Y-Y₁)/(Y₂-Y₁)*f(R₂)

 通过这样的处理，我们便可以计算出目标图像法 f(i,j)的像素值了，从而可以求出目标图像.

下面是Opencv的代码：

#include<opencv2opencv.hpp>
#include<opencv2corecore.hpp>
#include<opencv2highguihighgui.hpp>

using namespace std;
using namespace cv;

int main(){
    Mat src;
    src=imread("G:/save1.jpg",1);    //输入图片;
    if(src.empty()){
        return -1;
    }
    Mat dist=Mat((2*src.rows),(2*src.cols),CV_32FC3);        //目标图片，将原图放大两倍;

    //遍历目标图片的点，将目标图片的归溯到原图的点当中，若结果为浮点型，则按照算法计算；
    //归溯算法，原图大小为a*b，目标图大小m*n，i/x=a/m，j/y=b/n;

    float x,y;
    int Q11[2],Q21[2],Q12[2],Q22[2];          //Q11 Q12 Q21 Q22分别对应着与P点最为临近的四个点，P点为目标图点还原到原图的点的对应位置;
    float R1[3],R2[3];
    for(int i=0;i<dist.rows-1;i++){           //这里减2是因为对于(src.rows-1,src.cols-1)的位置对应的是（dist.rows-2,dits.cols-2),再大一点就会超过内存。
        for(int j=0;j<dist.cols-1;j++){
            x=(i+0.5)*0.5-0.5;               //通过加减0.5，将像素点移到中心点的位置，使放缩效果更好。
            y=(j+0.5)*0.5-0.5;

            Q11[0]=(int)x;
            Q12[0]=(int)x;
            Q21[0]=(int)x+1;
            Q22[0]=(int)x+1;

            Q11[1]=(int) y;
            Q21[1]=(int) y;
            Q12[1]=(int) y+1;
            Q22[1]=(int) y+1;

            // 插值法算法如下：
            // X1=(int)x; X2=(int)x+1; Y1=(int)y; Y2=(int)y+1;
            // f(R1)=(X2-X)/(X2-X1)*f(Q11)+(X-X1)/(X2-X1)*f(Q21);
            // f(R2)=(X2-X)/(X2-X1)*f(Q12)+(X-X1)/(X2-X1)*f(Q22);
            // f(i,j)=(Y2-Y)/(Y2-Y1)f(R1)+(Y-Y1)/(Y2-Y1)*f(R2);
            for(int m=0;m<3;m++){
                R1[m]=((Q21[0]-x)*src.at<Vec3b>(Q11[0],Q11[1])[m])+((x-Q11[0])*src.at<Vec3b>(Q21[0],Q21[1])[m]);
                R2[m]=((Q21[0]-x)*src.at<Vec3b>(Q12[0],Q12[1])[m])+((x-Q11[0])*src.at<Vec3b>(Q22[0],Q22[1])[m]);
                dist.at<Vec3f>(i,j)[m]=(Q12[1]-y)*R1[m]+(y-Q11[1])*R2[m];
            }
        }
    }
    imwrite("G:/save.jpg",dist);          //输出图片;
}