斐波那契数列
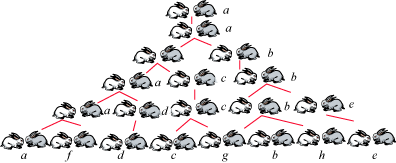
兔子问题:“假定一对大兔子每月能生一对小兔子,且每对新生的小兔子经过一个月可以长成一对大兔子,具备繁殖能力,如果不发生死亡,且每次均生下一雌一雄,问一年后共有多少对兔子?”
分析:第一个月兔子没有繁殖能力,所以还是一对;两个月后生下一对兔子,共有两对;三个月后,老兔子生下一对,小兔子还没有繁殖能力,所以一共是三对,以此类推,可以列出下表

表中1,1,2,3,5,8,13.....构成一个序列,这个数列有一个特点就是前两项之和等于后一项
数学函数定义:

---------------------------------------------------------------------------------------------------------------------
递归
public static long fib(int n){
/**
*fib递归算法
*时间复杂度O(N^2)
*空间复杂度O(N)
**/
return n<2?Math.max(n,0):fib(n-2)+fib(n-1);
}
循环
public static long fib(int n){
/**
*fib循环算法
*时间复杂度O(N)
*空间复杂度O(1)
**/
if(n<2)
return Math.max(n,0);
long fib1=1,fib2=0,fibN=0;
for(int i=1;i<n;i++){
fibN=fib1+fib2;
fib2=fib1;
fib1=fibN;
}
return fibN;
}
通项公式
方法一:利用特征方程(线性代数解法)
解得

则



解得


则
解得

public static long fib(int n){ /** *时间复杂度O(logN) *空间复杂度O(1) **/ return (long)(Math.pow(1+Math.sqrt(5)/2,n)-Math.pow(1-Math.sqrt(5)/2,n))/Math.sqrt(5)); }
参考:https://www.cnblogs.com/zkfopen/p/11245857.html
https://jasonkayzk.github.io/2020/02/25/Fibonacci序列生成算法的优化/
https://baike.baidu.com/item/斐波那契数列/99145?fr=aladdin