本文参考 https://www.cnblogs.com/chengxiao/p/6129630.html 感谢大佬精心绘图!
主要思想:
1、将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
2、将堆顶元素与末尾元素交换,将
最大元素"沉"到数组末端,同时接着重新调整堆的结构 3、继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序
每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆
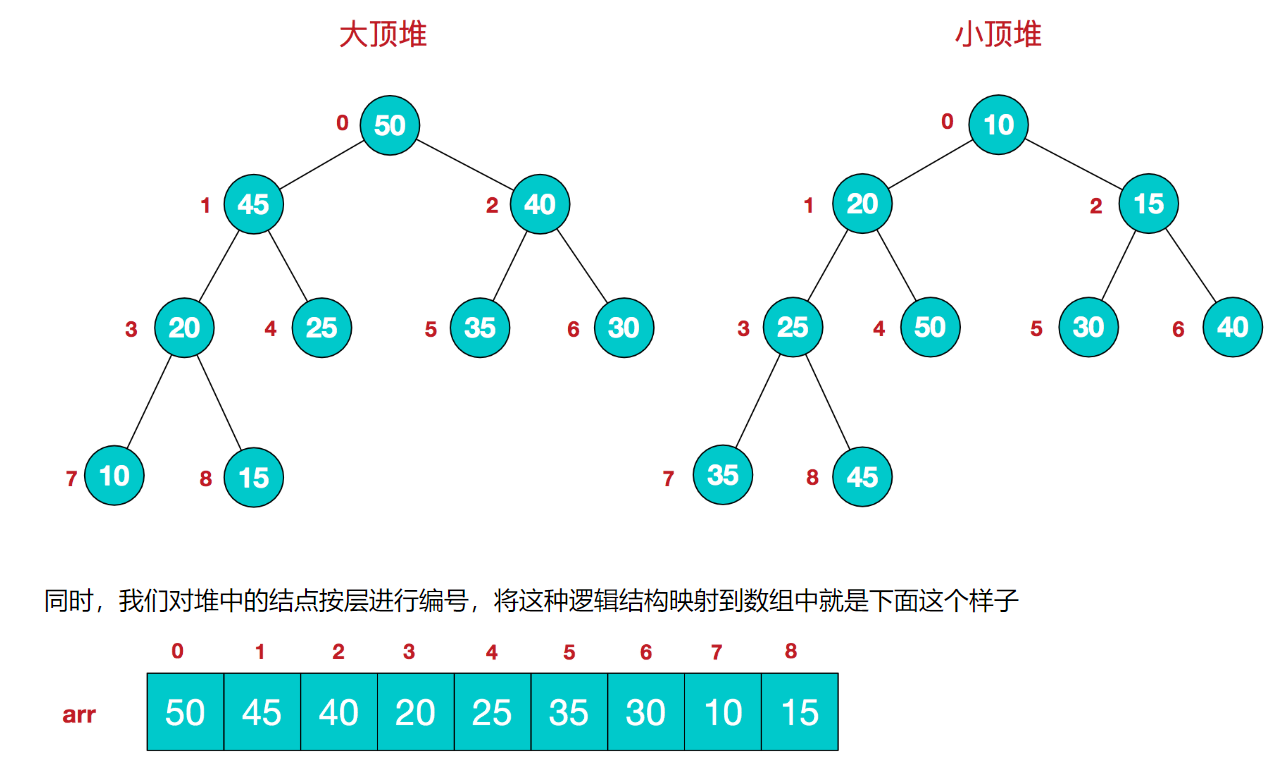
该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
二叉树相关知识:
第一个非叶子节点 m = arr.length / 2 -1
第一个非叶子节点的左孩子节点 n = 2 * m + 1
package com.jason.sort;
/**
* @Authot CodeDuck
* @Date 2020/7/17-13:20
*/
public class HeapSort {
public static void main(String[] args) {
int[] arr = {11, 7, 18, 3, 5, 4, 10, 9};
sort(arr);
for (int a : arr) {
System.out.println(a);
;
}
}
/**
* @Description: 堆排序
* @Param: arr数组
* @return: void
*/
public static void sort(int[] arr) {
// 1、构建大顶堆
for (int i = arr.length / 2 - 1; i >= 0; i--) {
// 从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(arr, i, arr.length);
}
// 2、调整堆结构+交换堆顶元素与末尾元素
for (int i = arr.length - 1; i > 0; i--) {
swap(arr, 0, i);
adjustHeap(arr, 0, i);
}
}
/**
* @Description: 调整为大顶堆
* @Param: arr数组
* @Param: i 所要调整的节点
* @Param: length:数组长度
* @return: void
*/
public static void adjustHeap(int[] arr, int i, int length) {
int temp = arr[i]; // 获取当前交换的节点val
for (int k = 2 * i + 1; k < length; k = 2 * k + 1) { // 获取当前节点的左孩子节点
// 若左孩子节点小于右孩子节点,k指向右孩子节点
if (k + 1 < length && arr[k] < arr[k + 1]) {
k++;
}
if (arr[k] > temp) { // 如果当前孩子节点大于父节点
arr[i] = arr[k]; // 将父节点的值 赋值于 被交换孩子节点
i = k; // 将 i 指向被交换孩子节点
} else {
break;
}
}
arr[i] = temp; // 将temp赋值于被交换孩子节点
}
/**
* @Description: 交换元素
* @Param: arr 元素组
* @Param: i,j数组下标
* @return: void
*/
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
堆排序是一种选择排序,整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。
建立N个元素的二叉堆花费时间:O(n)
在交换并重建堆的过程中,需交换n-1次,而重建堆的过程中,根据完全二叉树的性质,[log2(n-1),log2(n-2)...1]逐步递减,近似为
O(NlogN)因此,堆排序在面对最好和最坏的情况下都是稳定的