一个约瑟夫环问题
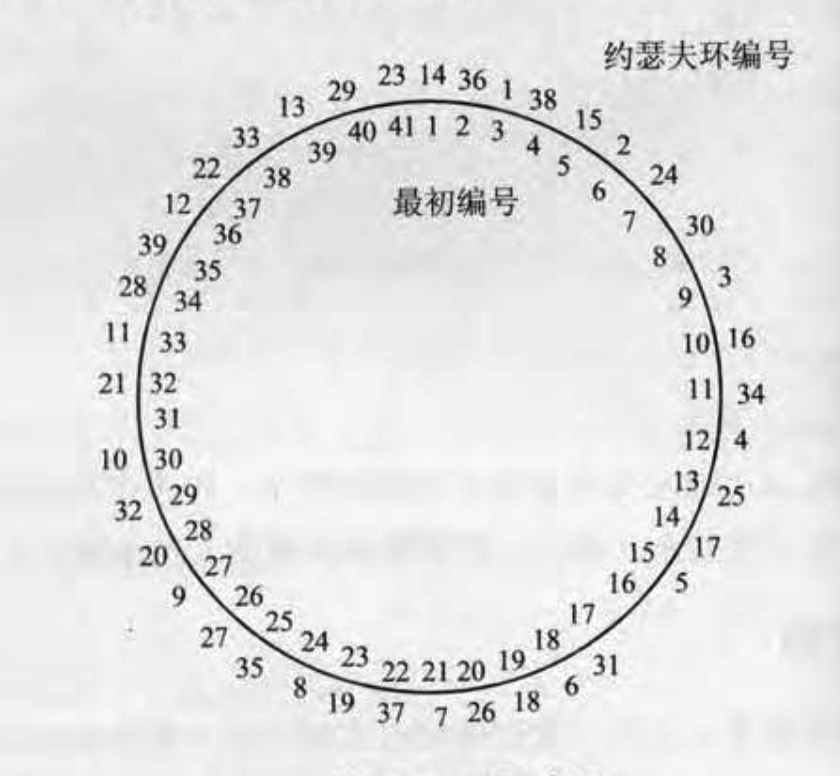
问题开始: 罗马人攻占了乔塔帕特,41个人藏在一个山洞躲过了这场浩劫。这41个人中,包括历史学家Josephus(约瑟夫)和特的一个朋友。剩余的39个人为了表示不向罗马人屈服,决定集体自杀。大家决定了一个自杀方案,所有这41个人围成一个圆圈,由第一个人开始顺时针报数,每报数为3的人就立刻自杀,然再由下一个重新开始报数,仍然是每报数为3的人立刻就自杀,。。。。,直到所有的人都自杀身亡位置。 约瑟夫和他的朋友并不想自杀,于是约瑟夫想到一个计策,他们两个同样参与到自杀的方案中,但是最后却躲过了自杀。请问,他们是怎么做到的? 先分析一下约瑟夫和他朋友想要躲过自杀,那么自杀到嘴壶一轮剩下三个人,且约瑟夫和他的朋友应该位于1和2的位置,这样就能躲过自杀, 首先将41个人排成一个环,内圈按顺时针的最初编号,外圈为每个人数到3的顺序,就是约瑟夫环号,如下图
下面是这个问题的代码实现,(java)
1package neuq.chao;
2 3 public class Josephus { 4 static final int Num = 41; 5 static final int KillMan =3; 6 static void josephus(int alive){ 7 //alive为要存活的人的个数 8 int man[] = new int[Num]; //声明一个数组 9 int pose = -1; //指针 10 int i = 0; 11 int count = 1; 12 while(count<=Num){ 13 do{ 14 pose = (pose+1)%Num; 15 if(man[pose]==0){ //等于0没有自杀 16 i++; 17 if(i==KillMan){ //数到3的人自杀 18 i=0; 19 break; 20 } 21 } 22 }while(true); 23 man[pose] = count; 24 System.out.printf("第%2d个自杀的人约瑟夫环号为:%2d",man[pose],pose+1); 25 if(count%2==1){ 26 System.out.printf("->"); 27 } 28 else{ 29 System.out.printf("-> "); //控制输出格式 30 } 31 count++; //自杀人加1 32 } 33 System.out.println("/n"); 34 System.out.printf("这%d需要存活的人的初始序号应排列在以下序号: ",alive ); 35 alive = Num - alive; 36 for(i=0;i<Num;i++){ 37 if(man[i]>alive){ //最后两个自杀的人存活 38 System.out.printf("初始编号为:%d", i+1); 39 } 40 } 41 System.out.printf(" "); 42 } 43 public static void main(String args[]){ 44 josephus(2); //演示 45 } 46 }
向以上问题我们可以统归为约瑟夫环(约瑟夫问题)是一个数学的应用问题:已知n个人(以编号1,2,3...n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;依此规律重复下去,直到圆桌周围的人全部出列。
只要对上述代码稍加修改即可形成对这一问题的统一解法