作为一名合格的程序员,最基本的,也是最经常使用的一些算法,我们将它放在数据结构与算法专栏最后几篇博文中,就是因为它十分重要并且对于刚接触数据结构与算法的同学来说,部分代码十分晦涩难懂,希望大家看完这两篇博文后能够对其重视,最终有所收获!
那么,言归正传,我们今天来进行我们代码的编写以及讲解:
在我们编程开始之前,我要声明一点,我们所有排序的结果有两种:升序以及降序,但是两种的主要处理思路是一样的,所以我们这两篇博文就通过以升序排列为基础来讲解这八大排序方法:
那么,所有准备都做好了,我们现在开始我们的主题——排序吧!
冒泡排序和选择排序是应该是我们到目前为止最熟悉的两种排序,那么,这篇博文就来讲解一下冒泡排序和选择排序以及它们的进阶版排序——堆排序和快速排序
一、冒泡排序(交换排序):
冒泡排序的基本原理是:
每一个数与它后面的数相比较,最终每一轮排完都会将未排序中最大(或最小)的数排在适当的位置。
那么,我们通过一个动态图来完整化我们上面的讲解:
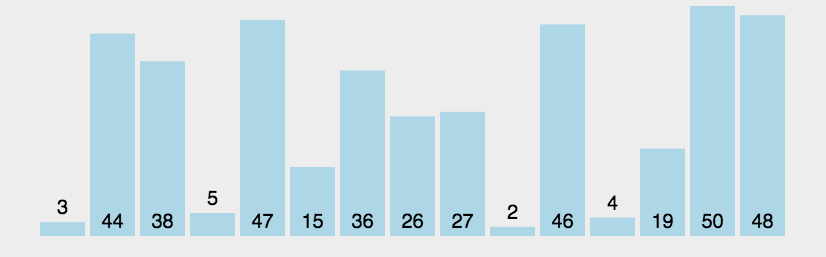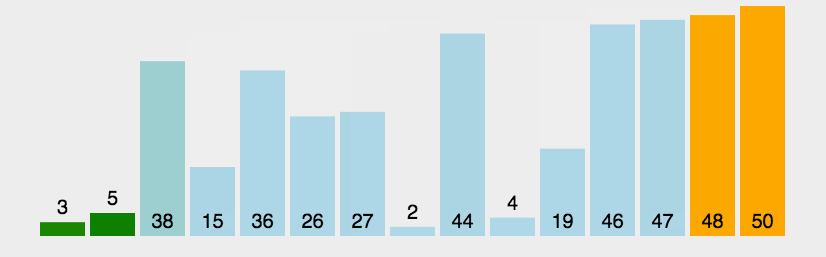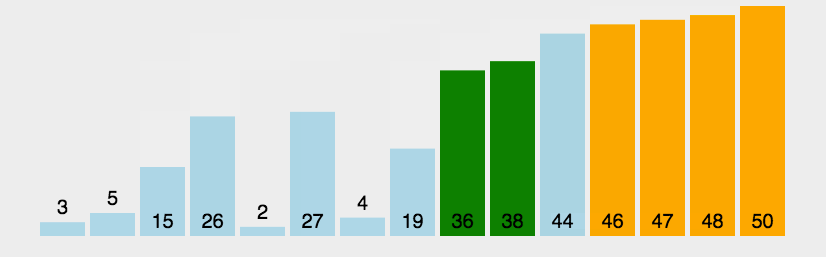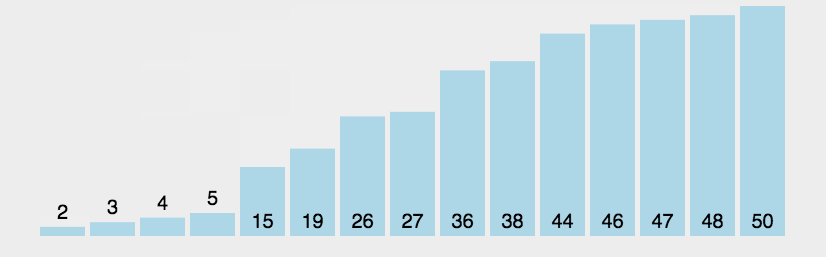
相关代码如下:
void exchangeSort(int *array, int count) {
int i;
int j;
int tmp;
for (i = count-1; i > 0; i--) {
for (j = 0; j < i; j++) {
if (array[j] > array[j+1]) {
tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
}
}
}
}
从上面的代码中我们可以看出,冒泡排序的时间复杂度时O(n^2)
那么,这种排序我们之前接触的时候可能会发现一件事,那就是就算都已经排好了顺序,但还是要排完所有的循环才能停止,这就导致代码的时间复杂度很高,所以我们来优化下冒泡排序,相关代码如下:
void exchangeSort(int *array, int count) {
int i;
int j;
int tmp;
boolean hasExchange;
for (i = count-1; i > 0; i--) {
for (hasExchange = FALSE, j = 0; j < i; j++) {
if (array[j] > array[j+1]) {
tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
hasExchange = TRUE;
}
}
if (!hasExchange) {
return;
}
}
}
我们设置了一个boolean类型的变量,这样,当我们顺序排好之后,就不会给hasExchange变量赋值为TRUE了,就能够跳出内层循环,然后由if判断为FALSE,跳出外层循环,这样,相比于我们之前所学的那个版本的冒泡排序,就可以在一定程度上降低代码的时间复杂度。
二、堆排序(冒泡排序*进阶版):
“堆”这个名词对于我们而言并不陌生,我们所用的calloc()函数所申请的空间,就是在堆空间内申请的空间,那么,大致原理如下:
本人之前的博文中提到过二叉树,而本人现在要讲解的这个排序算法,就是基于二叉树的基础二构建的算法。而且我们所用的还是“大根堆”,这个名词在本人的以往的博文中还未曾提到过,就在我们这篇博文中解释下:
“大根堆”——要求根存储的数值比它的左右孩子存储的数值大
我们首先先用所有的数构建一个二叉树,从第一个开始,从左到右依次填补满每一层,直至最后一层填补完成,举个例子,给出如下数:
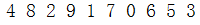
构建的二叉树如下:
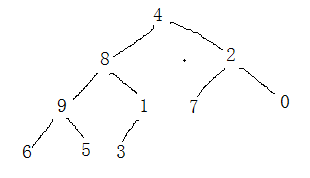
现在的二叉树肯定不是我们要的大根堆,那么,我们进行调整:
从叶子节点开始,从下往上,这样一轮下来,最大的数就会存在根节点,这时我们再将根节点和最后一个叶子节点交换数值,将存储最大数的节点(现在是最后一个叶子节点)从二叉树中取出,不参与之后的排序。然后往复上面的操作,这样就能按照降序将数组中的数先后取出,但是我们最后一个叶子节点的空间是未排数组的最后一个单元,也可以用与“大根堆”相反的“小根堆”进行操作,这样得到的排好的数的顺序的,而得到的“数组”是降序的
我们现在通过一张动态图来形象化我们的解释:
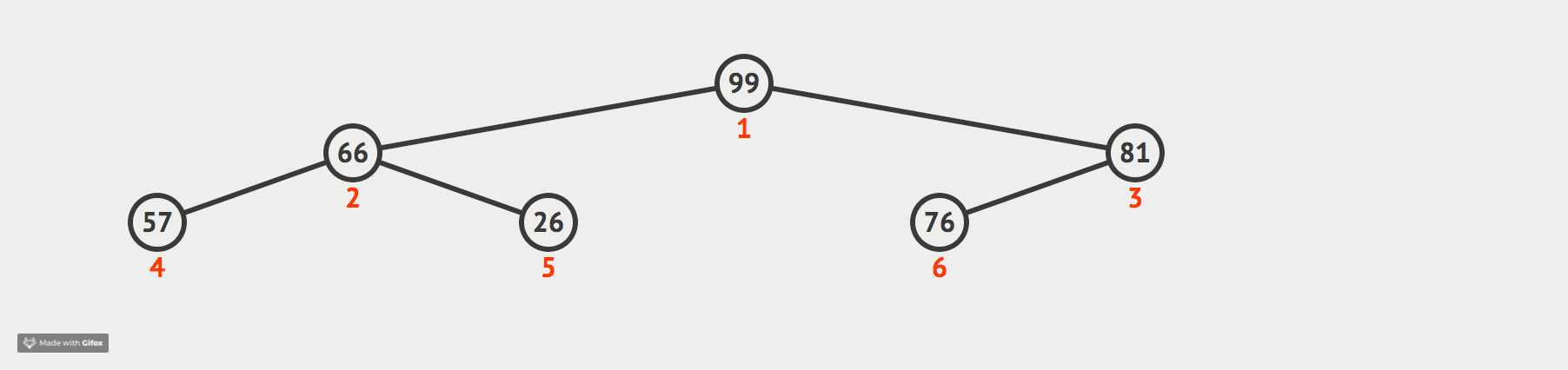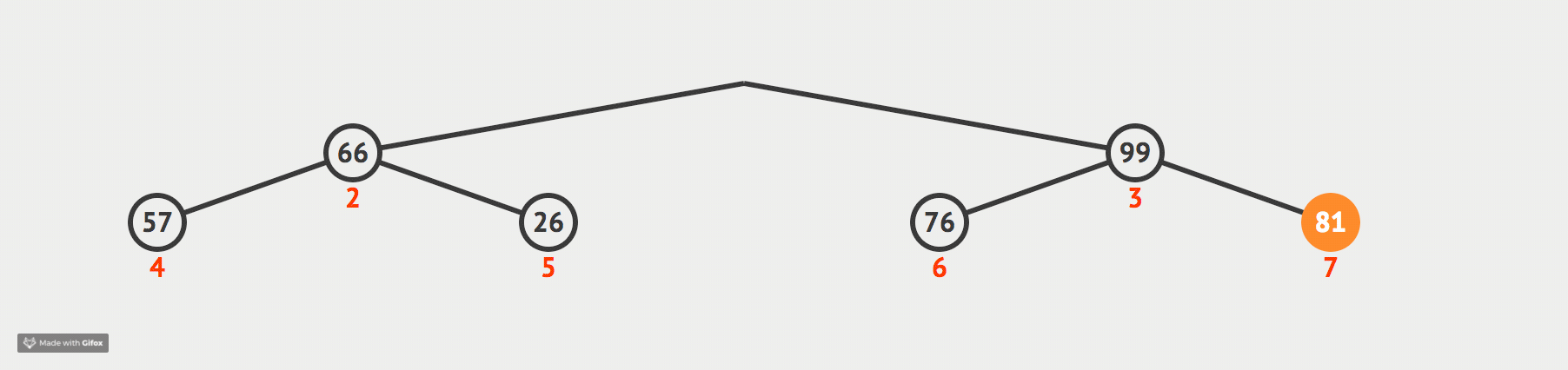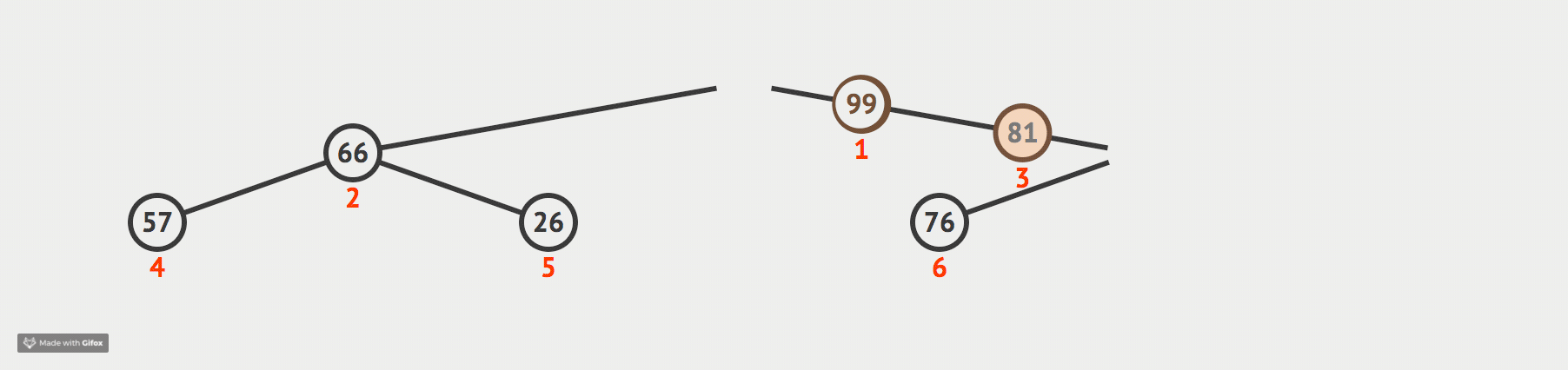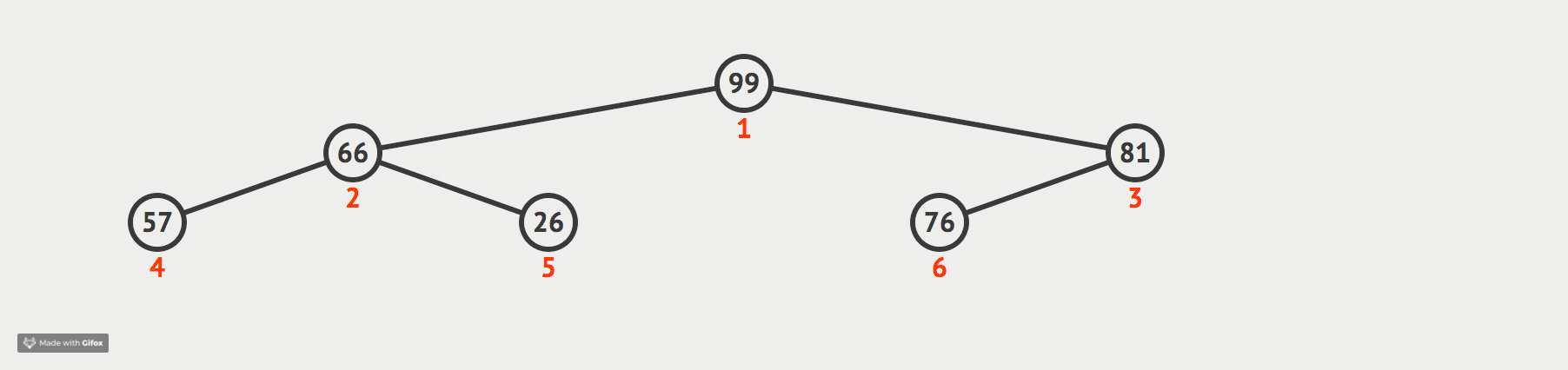
代码如下:
static void adjustHeap(int *array, int count, int root) {
int leftChildIndex;
int rightChildIndex;
int maxValueIndex;
int tmp;
while (1) {
leftChildIndex = 2*root + 1;
if (leftChildIndex >= count) {
return;
}
rightChildIndex = 2*root + 2;
maxValueIndex = rightChildIndex >= count ? leftChildIndex
: (array[leftChildIndex] > array[rightChildIndex]
? leftChildIndex : rightChildIndex);
maxValueIndex = array[root] > array[maxValueIndex] ? root : maxValueIndex;
if (root == maxValueIndex) {
return;
}
tmp = array[root];
array[root] = array[maxValueIndex];
array[maxValueIndex] = tmp;
root = maxValueIndex;
}
}
void heapSort(int *array, int count) {
int root;
int i;
int tmp;
for (root = count/2 - 1; root > 0; root--) {
adjustHeap(array, count, root);
}
for (i = 0; i < count - 1; i++) {
adjustHeap(array, count - i, 0);
tmp = array[0];
array[0] = array[count - 1 - i];
array[count - 1 - i] = tmp;
}
}
从上面的代码中我们可以看出,堆排序的时间复杂度时O(n* lgn)
这里对上面的代码做下解释:
第一个函数的类型前都有个static,意思是这个函数仅在该文件中使用,我们所编写的函数在接下来的代码中能够发现,提供给用户使用的只是这八大排序,至于构成这八大函数的子函数,不会提供给用户,这也是我们在数据结构与算法专题中要提到的,编写的.h的.c函数能够提供给外部使用的函数,在.h文件中声明;至于不能给外部使用的函数,就在.c文件中声明,我们在未来编程的过程中会了解到我们所做的工具函数和这里一样,并不是把所有的函数都提供给用户使用。
三、选择排序:
选择排序也是我们学到目前为止最熟悉的两种排序之一了,相对于冒泡排序,选择排序是用未排序的第一个数和后面的所有数相比,将比第一个数小的数和第一个数相交换,这样下来经过(count-1)次排列,我们就能完成对所有数的排列了。
这里我们通过一个动态图来使得我们的讲解更加形象:
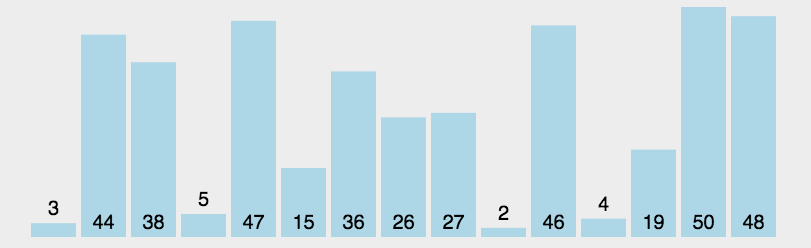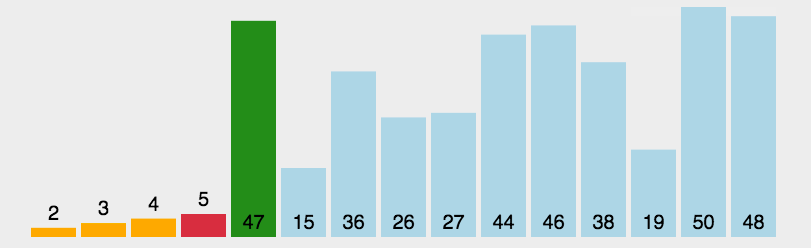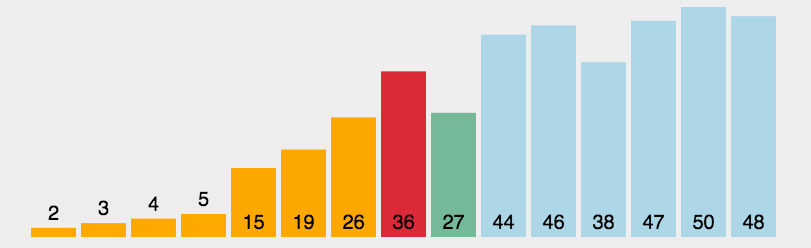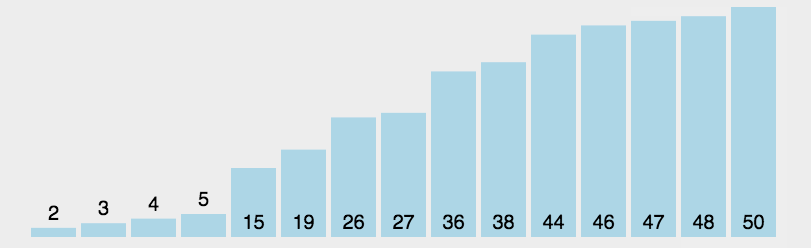
相关代码如下:
void chooseSort(int *array, int count) {
int i;
int j;
int minIndex;
int tmp;
for (i = 0; i < count-1; i++) {
for (minIndex = i, j = i+1; j < count; j++) {
if (array[minIndex] > array[j]) {
minIndex = j;
}
}
if (minIndex != i) {
tmp = array[i];
array[i] = array[minIndex];
array[minIndex] = tmp;
}
}
}
从上面的代码中我们可以看出,选择排序的时间复杂度时O(n^2)
这个排序的逻辑相对简单,我们在这里就不进行过多的解释了。
四、快速排序(选择排序*进阶版):
原理如下:
我们将一个数作为指标,分别从左边和右边遍历数组,从左遍历时将比它小的数放在它的左边,从右遍历时将比它大的数放在它右边,若遍历到同一个位置,就表示这轮排序结束。这样的话,一轮下来作为指标的数就放在了它应该在的地方。
在我们排完一轮之后,以这轮指标值为界限,将它左边的部分和右边的部分再次分别进行如此排列,直至排完所有数为止。
在这里我们通过一个动态图来使得讲解更加清晰:
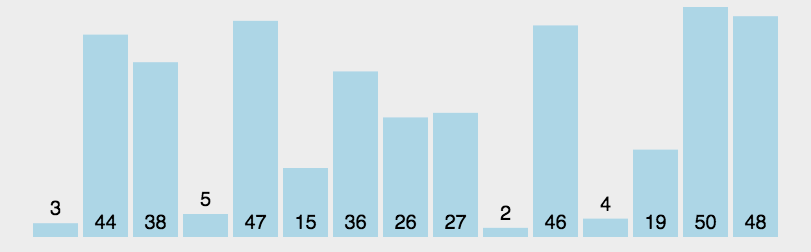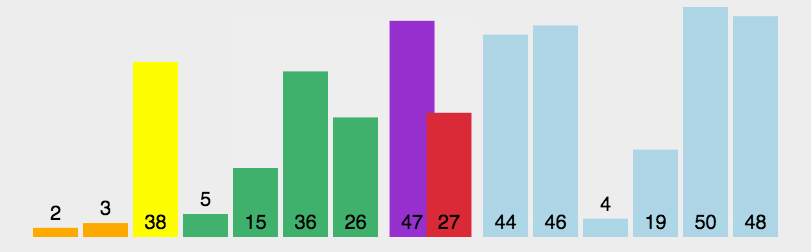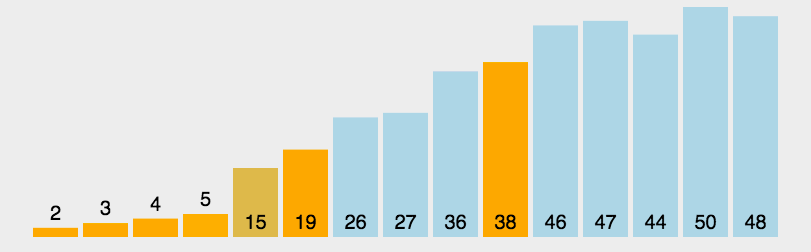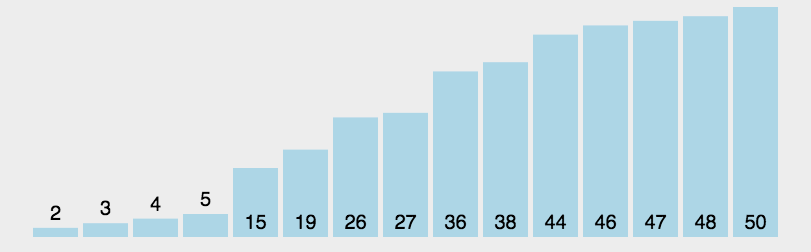
那么,现在我们来通过我们上面的讲解,编写代码:
static int qSortOnce(int *array, int start, int end) {
int i = start;
int j = end;
int tmp = array[i];
while(i<j) {
while(array[j] > tmp) {
j--;
}
if(i<j) {
array[i++]=array[j];
}
while(i < j && array[i] > tmp) {
i++;
}
if(i<j) {
array[j--]=array[i];
}
}
array[i]=tmp;
return i;
}
static void qSort(int *array, int start, int end) {
int middle;
if (start >= end) {
return;
}
middle = qSortOnce(array, start, end);
qSort(array, start, middle-1);
qSort(array, middle+1, end);
}
void quickSort(int *array, int count) {
qSort(array, 0, count-1);
}
从上面的代码中我们可以看出,快速排序的时间复杂度时O(n*logn)
这里对上面的代码做下解释:
1.第一个函数和第二个函数的类型前都有个static,和上面堆排序那里原因一样;
2.为什么要编写第三个函数呢?
因为我们之前的排序法和之后要编写的排序的代码,都会是同一种返回值和同样的参数,这样利于用户使用。其实最主要的一点是我们在篇首说过,我们会用到函数指针,所以我们要将所有的提供给外部的排序函数都写成一样的参数和返回值。
那么,我们这篇博文对于前四种排序的的介绍就结束了,
本人对于接下来两篇博文的安排是:
中篇:讲解之后四种排序法,并编写相关代码;
下篇:使用这些函数,并比较各种排序的时间复杂度,并且介绍一种十分强悍的调用这些函数的方式
所以,请持续观看本人的中篇——《八大排序 详解(中)》和下篇《八大排序 详解(下)》,
谢谢!!!